Quasi-birth and death processes of two-server queues with stalling

Abstract

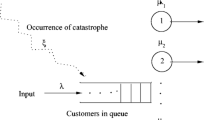
This paper investigates an optimal K-policy for a two-server Markovian queueing system $M/(M_1,M_2)/2/(B_1,B_2),$ with one fast server $S_1$ and one slow server $S_2$, using the matrix analytic method. Two buffers $B_1$ and $B_2$ are organized to form waiting lines of customers in which, buffer $B_1$ is of finite size $K(< \infty )$ and buffer $B_2$ is of infinite capacity. Buffer $B_1$ stalls customers who arrive when the system size (queue + service) is less than $(K+1)$ and dispatches a customer to the fast server $S_1$ only after $S_1$ completes its previous service. This K-policy is of threshold type which deals with controlling of informed customers and hence the customers have better choice of choosing the fast server routing through the buffer $B_1$. The $(K+2)$-nd customer who arrives when the number of customers present in the system is exactly $(K+1)$ has the Hobson’s choice of getting service from the slow server $S_2.$ Buffer $B_2$ accommodates other customers who arrive when the number of customers present in the system is $(K+2)$ or more and feeds them one after another to either buffer $B_1$ or the sever $S_2$ whichever event can first accept the customer at the head-of-the-line in $B_2$. Queue length processes of interest are (1) $q_1=\lim \limits _{t\rightarrow \infty }X_1(t)$ and (2) $q_2=\lim \limits _{t\rightarrow \infty }X_2(t)$, where $X_1$(t) represents the number of customers who are in the buffers $B_1$ and $B_2$ and also in the service with server $S_1$ at time ‘t’ and $X_2$(t) represents the number of customers available with server $S_2$ only. The bi-variate random sequence $\mathbf{X}(t)=(X_1(t),X_2(t))$ of the system size (queue $+$ service) forms a quasi-birth and death process (QBD). Steady state characteristics, and some of the performance measures such as the expected queue length, the probability that each server is busy etc are obtained. Numerical illustrations are provided based on the average cost function to explore the methodology of finding the best K-policy which minimizes the mean sojourn time of customers.

Appendix: Algorithm for computing the stationary probability vector \(\varvec{\Pi }\)

Linear reduction algorithm by cutting the levels off, starting from the upper level $L(K+1)$ and moving down to the lowest level L(0) : 

• 1. Let $\mathbf{U}^{(\mathbf{k}+\mathbf{1})}=\mathbf{A}_{(\mathbf{K}+\mathbf{1})}.$

• 2. Compute $\mathbf{U}^{(\mathbf{i})}= \mathbf{A}_\mathbf{1}+ \mathbf{A}_\mathbf{0}$$( - U^{(i+1)})^{-1} \mathbf{A}_\mathbf{2}$ for $i=K,(K-1),\ldots , 1$ and

  $\mathbf{U}^{(\mathbf{0})}=\mathbf{B}+ \mathbf{A}_\mathbf{0}$  $( - U^{(1)})^{-1}\;\mathbf{A}_\mathbf{2}.$

• 3. Solve ${\varvec{\Pi }_{\mathbf{0}}} \mathbf{U}^{\mathbf{0}} =0$, ${\varvec{\Pi }_{\mathbf{0}}} \mathbf{e} = 1$.

• 4. Compute $\varvec{\Pi }_\mathbf{i} = { \varvec{\Pi }_{\mathbf{i}-\mathbf{1}}}$$\mathbf{R}^{\mathbf{i}}$ for $i=1,2, \ldots ,(K+1).$ where $\mathbf{R^{i}}=\mathbf{A_0 ( - U^{(i)})^{-1}}$.

• 5. Normalize $\varvec{\Pi }$ by $\varvec{\Pi } = ( {\varvec{\Pi } \mathbf{1}})^{-1} \; \; { \varvec{\Pi }}.$

In the finite case, it is evident that the matrices ${ \mathbf U}^{(\mathbf{i})}$ depend on the levels since the upper bound $(K+1)$ is finite. Hence the matrix $(\mathbf{- U}^{(\mathbf{i})})^{\mathbf{-1}} A_2$ records the first passage time probabilities from L(i) to L(i − 1).

1.1 Alternative algorithm for computing the stationary probability vector $\varvec{\Pi }$ of the QBD process X(t)

For $i=0,1,2,\ldots ,K,$ the generator matrix of the restricted process $\mathbf X^i(t)$ on the set $S_i=\bigcup \limits _{n=i}^{K+1} L(n)$ is given by

(32)

and $\mathbf{Q^{K+1}=C_{K+1}}$, where the matrix ${ \mathbf C_i}$, for $i=1,2,\ldots ,K,$ records the rates of returning to the level ‘i’ before reaching the level ‘$i+1$’ starting from the level ‘i’ and are recursively defined as follows: ${ \mathbf C_0= B, C_i=A_1+A_2(-C_{i-1})^{-1}A_0 } \;\;\; \text {for}\;\;\; \, i=1, 2,\ldots , K, \mathbf{C_{K+1}=A_{K+1}+A_2(-C_K)^{-1}A_0.}$

It is noticed that the matrix $\mathbf{(-C_i^{-1}A_0)}$ records the first passage probabilities from level L(i) to $L(i+1).$ The Stationary probability vector $\varvec{\Pi }=(\Pi _0,\Pi _1,\Pi _2,\ldots ,\Pi _{K+1})$ is determined by

$$\begin{aligned}&\varvec{\Pi }_{\mathbf{K}+\mathbf{1}}{} \mathbf{C}_{\mathbf{K}+\mathbf{1}}=\mathbf{0} , \\&\quad {\varvec{\Pi }_{\mathbf{i}}= \varvec{\Pi }_{\mathbf{i}+\mathbf{1}}\,\mathbf{A}_\mathbf{2}(-\mathbf{C}_\mathbf{i})^{-\mathbf{1}} } \,\;\; \text {for}\,\;\; i=K,K-1,\ldots ,3,2, \;\; \text {and}\, 1 \\&\quad \sum \limits _{n=0}^{K+1}{\varvec{\Pi }_\mathbf{n}\,\mathbf{e}} = 1. \end{aligned}$$

1.2 Numerical illustration of steady state results for $K_0=3$, $\lambda =12.2,$ $\mu _1=10.0$ and $\mu _2=3.2$

(33)

(34)

(35)

$$\begin{aligned} {\varvec{\Pi }_\mathbf{0}}&= (\pi _{00}= 0.10936112, \pi _{01}= 0.01984482), {\varvec{\Pi }_\mathbf{0} \mathbf{e}}=0.12920593 \\{\varvec{\Pi }_\mathbf{1}}&= (\pi _{10}= 0.12707022, \pi _{11}=0.03056102), {\varvec{\Pi }_\mathbf{1} \mathbf{e}}=0.15763124 \\{\varvec{\Pi }_\mathbf{2}}&= (\pi _{20}= 0.13889580, \pi _{21}= 0.05341432), {\varvec{\Pi }_\mathbf{2} \mathbf{e}}= 0.19231012\\{\varvec{\Pi }_\mathbf{3}}&= (\pi _{30}= 0.13623042, \pi _{31}= 0.09838791), {\varvec{\Pi }_\mathbf{3} \mathbf{e}}= 0.23461833\\{\varvec{\Pi }_\mathbf{4}}&= (\pi _{40}= 0.10149450, \pi _{41}= 0.18473980), {\varvec{\Pi }_\mathbf{4} \mathbf{e}}= 0.2862343\\\end{aligned}$$

$$\begin{aligned} \left( \sum _{\mathbf{i}=0} ^{4}\varvec{\pi }_{\mathbf{i}0}, \sum _{\mathbf{i}=0}^{4} \varvec{\pi }_{i1}\right) = (b_{0}=0.61305206 , b_{1}=0.38694787) \end{aligned}$$