Wigner’s effective mathematics and contradiction

Abstract

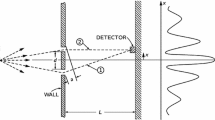
Complex numbers are basic. An inconsistency would question Wigner’s unreasonable effectiveness of mathematics. A vehicle to study this question is Kirchoff’s scalar diffraction theory. In the paper, an inconsistency in the real phase angle of a complex number is presented. When this inconsistency is introduced in Kirchoff’s theory, we can study its influence on the experimental success of this theory. There are no a priori reasons to include or exclude real phase angles. Referring to Wigner’s idea of the role of mathematics in empirical science, an experiment can provide more insight. In the experiment, a weak intensity, small wavelength source can be employed. When the contradictory phase angle is excluded, a nonzero diffraction amplitude appears physically possible. If it is included, this amplitude vanishes.

A: Appendix

Here, the R program is presented to support that

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{\sin (1/n)}{ \sqrt{ 1+(1+\sin (1/n))^2-2\cos (1/n)(1+\sin (1/n)) } } =\frac{1}{\sqrt{2}} \end{aligned}$$