Skip to main content
SpringerLink
Log in

Numerical Treatment for the Class of Time Dependent Singularly Perturbed Parabolic Problems with General Shift Arguments

  • Original Research
  • Published:
Differential Equations and Dynamical Systems Aims and scope Submit manuscript

Abstract

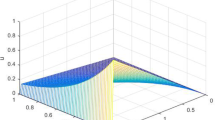
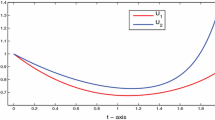
In this paper we design two numerical schemes for solving a class of time dependent singularly perturbed parabolic convection–diffusion problems with general shift arguments in the reaction term. The discretization in both the directions is based on finite difference scheme. Special type of mesh and interpolation is used to tackle the terms containing shifts. The earlier numerical schemes for the considered problem are restricted to the case of small delay and advance arguments while in practical situations these shift arguments can be of arbitrary size (i.e., may be big or small enough in size). In this paper we propose two numerical schemes which work in both the situations i.e., when shifts are big or small enough in size. An extensive amount of analysis is presented to show the linear convergence in space and time of both the schemes. Some numerical results are given to confirm the predicted theory and to show the effect of shifts on the solution.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Ansari, A., Bakr, S., Shishkin, G.: A parameter-robust finite difference method for singularly perturbed delay parabolic partial differential equations. J. Comput. Appl. Math. 205(1), 552–566 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bashier, E., Patidar, K.: A second-order fitted operator finite difference method for a singularly perturbed delay parabolic partial differential equation. J. Differ. Equ. Appl. 17(05), 779–794 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bashier, E., Patidar, K.C.: An almost second order fitted mesh numerical method for a singularly perturbed delay parabolic partial differential equation. Neural Parallel Sci. Comput. 18(2), 137–154 (2010)

    MathSciNet  MATH  Google Scholar 

  4. Bashier, E.B., Patidar, K.C.: A novel fitted operator finite difference method for a singularly perturbed delay parabolic partial differential equation. Appl. Math. Comput. 217(9), 4728–4739 (2011)

    MathSciNet  MATH  Google Scholar 

  5. Clavero, C., Jorge, J., Lisbona, F.: A uniformly convergent scheme on a nonuniform mesh for convection–diffusion parabolic problems. J. Comput. Appl. Math. 154(2), 415–429 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  6. Farrell, P., Hegarty, A.: On the determination of the order of uniform convergence. In: Proceedings of the 13th IMACS World Congress on Computational and Applied Mathematics (IMACS, 1991), pp. 501–502 (1991)

  7. Kaushik, A., Sharma, K., Sharma, M.: A parameter uniform difference scheme for parabolic partial differential equation with a retarded argument. Appl. Math. Modell. 34(12), 4232–4242 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  8. Kellogg, R.B., Tsan, A.: Analysis of some difference approximations for a singular perturbation problem without turning points. Math. Comput. 32(144), 1025–1039 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  9. Kumar, D., Kadalbajoo, M.K.: A parameter-uniform numerical method for time-dependent singularly perturbed differential-difference equations. Appl. Math. Model. 35(6), 2805–2819 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  10. Ladyzhenskaia, O.A., Solonnikov, V.A., Ural’ceva, N.N.: Linear and Quasi-Linear Equations of Parabolic type, vol. 23. American Mathematical Society, Providence (1988)

  11. Miller, J.J.H., O’Riordan, E., Shishkin, G.I.: Fitted Numerical Methods for Singular Perturbation Problems: Error Estimates in the Maximum Norm for Linear Problems in One and Two Dimensions. World Scientific Publishing Co. Inc., River Edge (1996)

    Book  MATH  Google Scholar 

  12. Musila, M., Lánskỳ, P.: Generalized stein’s model for anatomically complex neurons. Biosystems 25(3), 179–191 (1991)

    Article  Google Scholar 

  13. Ramesh, V., Kadalbajoo, M.K.: Upwind and midpoint upwind difference methods for time-dependent differential difference equations with layer behavior. Appl. Math. Comput. 202(2), 453–471 (2008)

    MathSciNet  MATH  Google Scholar 

  14. Roos, H.G., Stynes, M., Tobiska, L.: Robust Numerical Methods for Singularly Perturbed Differential Equations: Convection–Diffusion-Reaction and Flow Problems, vol. 24. Springer, Berlin (2008)

    MATH  Google Scholar 

Download references

Acknowledgments

The work of the first author was supported by U.G.C. (Letter No. F.17-7(J)/08(SA-1) dated 01-Feb-2012) New Delhi, India. The work of the second author was supported by the Research and Development grant scheme 2014–2015 of University of Delhi, Delhi under Grant No. RC/2014/6820.

Author information

Authors and Affiliations

  1. Department of Mathematics, Panjab University, Chandigarh, India

    Komal Bansal

  2. Department of Mathematics, University of Delhi, New Delhi, India

    Pratima Rai

  3. Department of Mathematics, South Asian University, New Delhi, India

    Kapil K. Sharma

Authors
  1. Komal Bansal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pratima Rai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kapil K. Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Komal Bansal.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bansal, K., Rai, P. & Sharma, K.K. Numerical Treatment for the Class of Time Dependent Singularly Perturbed Parabolic Problems with General Shift Arguments. Differ Equ Dyn Syst 25, 327–346 (2017). https://doi.org/10.1007/s12591-015-0265-7

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12591-015-0265-7

Keywords

Mathematics Subject Classification

Search

Navigation