Introduction

Valve regurgitation, the backward flow in the heart when a cardiac valve does not completely close shut, has been found to have a significant effect on cardiac function [1]. Cardiac output in a regurgitant heart depends on regurgitant volume [2], an indicator of the severity of regurgitation. While research has focused on determining regurgitant volume using medical imaging techniques [3, 4], the effect of regurgitant volume on ventricular mechanical function has not been previously established. Understanding the changes in ventricular wall mechanics resulting from volume overload or underload caused by valvular regurgitation is of major clinical significance because it will allow the researchers to obtain a complete picture of the mechanisms that underlie ventricular remodeling and the progression of heart failure (HF) [5].

The goal of this study was to use a computational model of the heart to examine the effect of valvular regurgitation on ventricular mechanics. For this purpose, the 3D electromechanical model of the failing canine ventricles used in our previous studies [6, 7] was coupled with a lumped-parameter model of valvular regurgitation and the vascular system. Since patients with valvular regurgitation typically exhibit congestive HF and low cardiac output [8], the ventricular model was developed to represent the conditions of HF. Simulation studies were performed for different levels of severity of aortic and mitral regurgitation (AR and MR).

Methods

Ventricular mechanics model

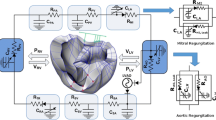
To achieve the goals of this study, we used an MRI-based electromechanical model of the failing canine ventricles developed previously by us [6, 7]. The ventricular geometry and fiber and laminar sheet architecture of the model were constructed from high-resolution MRI and diffusion tensor MRI scans of canine ventricles in dyssynchronous heart failure (DHF). The model consisted of coupled electrical and mechanical components and a lumped-parameter representation of the circulatory system (Fig. 1). The ventricular mechanics component was based on the continuum mechanics equations, with the myocardium assumed to be an orthotropic, hyperelastic, nearly incompressible material defined by an exponential strain energy function. The mechanics model of the ventricles comprised 356 nodes and 172 elements in terms of Hermite polynomial interpolation. The local electrical activation times obtained in our previous paper [9] were mapped onto the computational mesh of the DHF canine ventricles. The electromechanical model incorporated the biophysical representation of cardiac myofilament dynamics by Rice et al. [10].

Fig. 1
figure 1

Schematic diagram of the 3D finite-element ventricular electromechanical model coupled with the circulatory model. P RV right ventricular pressure; C LV left ventricular compliance; C RV right ventricular compliance; V RV right ventricular volume; P LV left ventricular pressure; V LV left ventricular volume; R PA pulmonary artery resistance; C PA pulmonary artery compliance; R PV pulmonary vein resistance; C PV pulmonary vein compliance; R MI forward resistance of mitral valve; R MI,Leak leakage resistance of mitral valve; C LA left atrial compliance; R AO forward resistance of aortic valve; R AO,Leak leakage resistance of aortic valve; R SA systemic artery resistance; C SA systemic artery compliance; R SV systemic vein resistance; C SV systemic vein compliance; R TR tricuspid valve resistance; C RA right atrium compliance; and R PU pulmonary valve resistance

Full size image

Remodeling of electromechanical properties associated with HF was implemented by changing parameters in the electromechanical model, so that previous experimental observations [11–13] were matched. Electrical conductivities were reduced by 30 % [11], whereas the passive scaling constant of the strain-energy function was increased five times the normal value to represent increased stiffness of the failing myocardium [12]. To incorporate systolic dysfunction, we reduced the peak calcium concentration in the failing cardiomyocyte to 70 % of the value in healthy myocytes [13]. A similar approach was used in recent publications [6, 7, 14, 15].

Model of valve regurgitation

To model MR and AR, two additional branches were added to both the aortic and the mitral compartments in the lumped-parameter model (Fig. 1). One branch had a forward diode to represent forward flow, and the other had a backward diode to represent leakage flow; the diodes had different resistance values. Regurgitant flow dynamics through the mitral and aortic valves were represented by the following equations:

$$Q_{MI} = \left\{ \begin{gathered} \frac{{P_{LA} - P_{LV} }}{{R_{MI} }}\quad {\text{when}}\;P_{LA} > P_{LV} \hfill \\ \frac{{P_{LA} - P_{LV} }}{{R_{{MI,{\text{Leak}}}} }} = \frac{{P_{LA} - P_{LV} }}{{R_{MI} }} \times \frac{SF}{100}\;\quad {\text{when}}\;P_{LA} \le P_{LV} \hfill \\ \end{gathered} \right.$$
(1)
$$Q_{AO} = \left\{ \begin{gathered} \frac{{P_{LV} - P_{AO} }}{{R_{AO} }}\quad {\text{when}}\;P_{LV} > P_{AO} \hfill \\ \frac{{P_{LV} - P_{AO} }}{{R_{{AO,{\text{Leak}}}} }} = \frac{{P_{LV} - P_{AO} }}{{R_{AO} }} \times \frac{SF}{100}\quad {\text{when}}\;P_{LV} \le P_{AO} \hfill \\ \end{gathered} \right.$$
(2)

where Q, P, and R denote flow rate (mL/min), pressure (mmHg), and flow resistance (mmHg min/mL), respectively. The subscripts MI, AO, LV, LA, and Leak correspond to the mitral valve, aortic valve, left ventricle, left atrium, and leakage, respectively. To quantify regurgitation severity, we introduced a scale to index blood leakage through the valves.

Simulation protocol

Severity of regurgitation was changed from 0 % (baseline state) to 10 % (severe regurgitation) in 1 % increments. For every case, the simulation was executed for 20 s, to ensure that, for the given degree of regurgitation, cardiovascular responses such as blood pressure, flow, and volume reached nearly steady state in each compartment. To analyze the effect of regurgitation on ventricular wall mechanics, we computed the changes in ventricular tension, strain, stroke work, stroke volume, and regurgitant volume for different values of regurgitation severity.

Results

Figure 2 shows the calculated transmural distribution of fiber strain at end-diastole and tension at end-systole for a failed heart without valvular regurgitation, as well as for a DHF hearts with 2 and 10 % AR, and with 2 and 10 % MR. Systolic tension in the LV septum and free wall was significantly lower for MR than for AR (Fig. 2b). However, end-diastolic strain was increased under AR and MR conditions; it was slightly higher in AR than in MR (Fig. 2a). In the MR case, the increased amount of ejected blood from the LV during systole caused a decrease in LV volume, reducing end-systolic tension, as expected from the Frank-Starling law (Fig. 2b).

Fig. 2
figure 2

Transmural distribution of strain at end-diastole and tension at end-systole in the dyssynchronously failing canine ventricles under aortic and mitral valve regurgitation conditions. AR aortic regurgitation; MR mitral regurgitation. Here, Baseline indicates DHF without valvular regurgitation

Full size image

Figure 3 illustrates the LV pressure–volume relationships for different degrees of AR and MR. As AR severity increased, the difference between systolic and diastolic pressure decreased (Fig. 3a). End-diastolic volume (EDV) increased significantly, whereas end-systolic volume (ESV) decreased slightly, thereby forming a horizontally extended pressure–volume loop.

Fig. 3
figure 3

Left ventricular pressure–volume loops for different degrees of regurgitation severity: a from 0 % aortic regurgitation (AR) to 10 % AR in 1 % increments. b from 0 % mitral regurgitation (MR) to 10 % MR in 1 % increments

Full size image

Figure 4 describes changes in regurgitant volume, stroke work, and stroke volume for different degrees of AR and MR. Regurgitant volume increased sharply at low levels of regurgitant severity, but increased commensurate with greater AR and MR severity (Fig. 4a). Interestingly, as regurgitant volume increased, stroke work decreased for MR, whereas regurgitant volume initially increased but subsequently decreased for AR (Fig. 4b). Stroke volume decreased in both AR and MR commensurate with increased regurgitant volume (Fig. 4c). Stroke work is the area within the pressure–volume loop. In general, stroke volume is calculated by subtracting ESV from EDV in the pressure–volume loop. However, under regurgitation conditions, practical SV is not equal to EDV–ESV. Therefore, we computed practical SV using arterial blood flow during a single cycle. SV and the ejection fraction, calculated according to this method, are shown in Fig. 4c. EDV–ESV refers to the degree of ventricular movement rather than to ventricular stroke volume.

Fig. 4
figure 4

a Regurgitant volume as a function of regurgitant severity; b left ventricular stroke work; and c stroke volume and ejection fraction as a function of regurgitant volumes under aortic and mitral regurgitation conditions; d left ventricular stroke volume as a function of left ventricular stroke work. AR aortic regurgitation; MR mitral regurgitation; SV stroke volume; EF ejection fraction; RV regurgitant volume; RF regurgitant fraction

Full size image

To estimate cardiac output, practical SV was obtained using arterial blood flow rather than the amount of ventricular movement, i.e., EDV–ESV. The relationship between practical stroke volume and stroke work is illustrated in Fig. 4d. Under identical stroke volume conditions, stroke work was greater under the AR compared with the MR condition, i.e., the ventricle consumed more energy under AR conditions.

Discussion

This study examined the effect of valvular regurgitation on ventricular mechanics using a computational model of the heart consisting of a 3D electromechanical representation of the DHF canine ventricles [6, 7]. This study examined the effect of valvular regurgitation on ventricular mechanics using a computational model of the heart consisting of a 3D electromechanical representation of the DHF canine ventricles [6, 7] coupled with a lumped-parameter model of valvular regurgitation and the vascular system. We simulated valvular regurgitation under physiologically normal heart as well as failed heart condition. However, the difference between the results of the two simulations was negligible. Therefore, we presented only the HF case.

We observed that end-systolic tension in the septum and LV free wall was significantly lower under MR than under AR conditions. The lower left ventricular pressure (Fig. 3) that characterizes the MR condition explains this phenomenon. During systole, reduced outflow resistance in MR induces more rapid exhaustion of blood in the LV, with concomitantly reduced systolic pressure in the LV. Therefore, because reduced mechanical load is applied to left ventricular myocytes, the LV can pump blood with less tension in the septum and LV free wall.

Stroke work in AR was higher than that in MR, whereas the difference in stroke volume between the two conditions was small, indicating that AR may induce worse pumping efficiency than MR in terms of consumed energy and performed work. The detailed investigation of ventricular mechanics under regurgitation conditions presented here was made possible by the use of a 3D ventricular model [4], a significant advance over previous lumped-parameter and one-dimensional models of the cardiovascular system [16]. Since the mechanical response evoked by LV volume overload or underload in valvular regurgitation can lead to ventricular remodeling and HF, understanding the changes in ventricular mechanics in the presence of regurgitant flow could have important clinical implications.

The significant decrease of ESV for severe AR, evident from the LV pressure–volume loop (Fig. 3a), could lead to congestive HF [4]. Stroke work, defined as the work performed by the ventricle to eject blood into the aorta (and calculated as the area within the pressure–volume loop) corresponds to LV energy consumption, whereas stroke volume corresponds to the useful work performed by the LV. As MR severity increased, both LV stroke work and stroke volume decreased, indicating that the LV both consumed less contractile energy and performed less useful work. In terms of stroke volume, the difference between the AR and MR conditions was not significant (Fig. 4c). However, stroke work was significantly greater under AR than MR conditions. Based on these results, we suggest that, because AR patients’ hearts perform a greater amount of stoke work than to MR hearts (Fig. 4b) and because AR and MR stroke volumes are similar (Fig. 4c), AR patients should exhibit decreased pumping efficiency compared with MR patients (Fig. 4d).

There are several limitations of the present study. First, we used an electromechanical model of DHF canine ventricles, which have mechanical characteristics somewhat different from those of the failing human ventricles. We limited the simulation conditions with the fixed preload and afterload. As Vendelin et al. [17] demonstrated, the pressure–volume loops computed by varying pre- and afterloads are useful to assess the mechanical characteristics of the LV. However, the basic characteristics of the results will not change even though preload and afterload are modified. In addition, a lumped-parameter representation of valvular regurgitation was used to reduce the complexity of the model. These limitations are not expected to significantly alter the main findings of this study.