Skip to main content
SpringerLink
Log in

On the choice of hyper-parameters of artificial neural networks for stabilized finite element schemes

  • Published:
International Journal of Advances in Engineering Sciences and Applied Mathematics Aims and scope Submit manuscript

Abstract

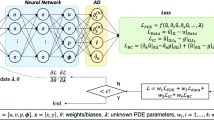
This paper provides guidelines for an effective artificial neural networks (ANNs) design to aid stabilized finite element schemes. In particular, ANNs are used to estimate the stabilization parameter of the streamline upwind Petrov–Galerkin (SUPG) stabilization scheme for singularly perturbed problems. The effect of the artificial neural network (ANN) hyper-parameters on the accuracy of ANNs is found by performing a global sensitivity analysis. First, a Gaussian process regression metamodel of the artificial neural networks is obtained. Next, analysis of variance is performed to obtain Sobol’ indices. The total-order Sobol’ indices identify the hyper-parameters having the maximum effect on the accuracy of the ANNs. Furthermore, the best-performing and the worst-performing networks are identified among the candidate ANNs. Our findings are validated with the help of one-dimensional test cases in the advection-dominated flow regime. This study provides insights into hyper-parameters’ effect and consequently aids in building effective ANN models for applications involving nonlinear regression, including estimation of SUPG stabilization parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

References

  1. Abgrall, R., Ricchiuto, M.: High Order Methods for CFD. Wiley, Hoboken (2017)

    Book  Google Scholar 

  2. Aimone, J.B., Parekh, O., Severa, W.: Neural computing for scientific computing applications: more than just machine learning. In: Proceedings of the Neuromorphic Computing Symposium, NCS ’17. Association for Computing Machinery, New York, NY, USA (2017). https://doi.org/10.1145/3183584.3183618

  3. Brooks, A.N.T.: Streamline upwind/petrov-galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier–Stokes equations. Comput. Methods Appl. Mech. Eng. 32(1–3), 199–259 (1982). https://doi.org/10.1016/0045-7825(82)90071-8

    Article  MathSciNet  MATH  Google Scholar 

  4. Barron, A.R.: Universal approximation bounds for superpositions of a sigmoidal function. IEEE Trans. Inf. Theory 39(3), 930–945 (1993). https://doi.org/10.1109/18.256500

    Article  MathSciNet  MATH  Google Scholar 

  5. Baudin, M., Dutfoy, A., Iooss, B., Popelin, A.L.: OpenTURNS: an industrial software for uncertainty quantification in simulation, pp. 1–38. Springer, Cham (2016)

    Google Scholar 

  6. Behzadi, F., Newman, J.C.: A semi-discrete SUPG method for contaminant transport in shallow water models. Procedia Comput. Sci. 80, 1313–1323 (2016). https://doi.org/10.1016/j.procs.2016.05.476

    Article  Google Scholar 

  7. Bochev, P.B., Gunzburger, M.D., Shadid, J.N.: Stability of the SUPG finite element method for transient advection-diffusion problems. Comput. Methods Appl. Mech. Eng. 193(23–26), 2301–2323 (2004). https://doi.org/10.1016/j.cma.2004.01.026

    Article  MathSciNet  MATH  Google Scholar 

  8. Brooks, A.N., Hughes, T.J.R.: Streamline upwind/Petrov–Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier–Stokes equations. Comput. Methods Appl. Mech. Eng. 32, 199–259 (1982)

    Article  MathSciNet  Google Scholar 

  9. Brunton, S.L., Noack, B.R., Koumoutsakos, P.: Machine learning for fluid mechanics. Ann. Rev. Fluid Mech. 52(1), 477–508 (2020). https://doi.org/10.1146/annurev-fluid-010719-060214

    Article  MATH  Google Scholar 

  10. Curtin, R.R., Cline, J.R., Slagle, N.P., March, W.B., Ram, P., Mehta, N.A., Gray, A.G.: MLPACK: a scalable C++ machine learning library. J. Mach. Learn. Res. 14, 801–805 (2013)

    MathSciNet  MATH  Google Scholar 

  11. Curtin, R.R., Edel, M., Lozhnikov, M., Mentekidis, Y., Ghaisas, S., Zhang, S.: Mlpack 3: a fast, flexible machine learning library. J. Open Source Softw. 3(726), 10 (2018). https://doi.org/10.21105/joss.00726

    Article  Google Scholar 

  12. Cybenko, G.: Approximation by Superpositions of a Sigmoidal Function. Math. Control Signals Syst. 2, 303–314 (1989)

    Article  MathSciNet  Google Scholar 

  13. Cybenko, G.: Neural networks in computational science and engineering. IEEE Comput. Sci. Eng. 3(1), 36–42 (1996). https://doi.org/10.1109/99.486759

    Article  Google Scholar 

  14. Discacciati, N., Hesthaven, J.S., Ray, D.: Controlling oscillations in high-order discontinuous Galerkin schemes using artificial viscosity tuned by neural networks. J. Comput. Phys. 409, 109304 (2020). https://doi.org/10.1016/j.jcp.2020.109304

    Article  MathSciNet  MATH  Google Scholar 

  15. Burman, E.: Consistent supg-method for transient transport problems: stability and convergence. Comput. Methods Appl. Mech. Eng. 199(17–20), 1114–1123 (2010). https://doi.org/10.1016/j.cma.2009.11.023

    Article  MathSciNet  MATH  Google Scholar 

  16. Burman, E.P.: Edge stabilization for galerkin approximations of convection-diffusion-reaction problems. Comput. Methods Appl. Mech. Eng. 193(15–16), 1437–1453 (2004). https://doi.org/10.1016/j.cma.2003.12.032

    Article  MathSciNet  MATH  Google Scholar 

  17. Burman, E., Fernandez, M.P.: Continuous interior penalty finite element method for Oseen’s equations. SIAM J. Numer. Anal. 44(3), 1248–1274 (2006). https://doi.org/10.1137/040617686

  18. Fernández-Navarro, F., Carbonero-Ruz, M., Alonso, D.B., Torres-Jimenez, M.: Global sensitivity estimates for neural network classifiers. IEEE Trans. Neural Netw. Learn. Syst. 28(11), 2592–2604 (2017). https://doi.org/10.1109/TNNLS.2016.2598657

    Article  MathSciNet  Google Scholar 

  19. Fock, E.: Global sensitivity analysis approach for input selection and system identification purposes—a new framework for feedforward neural networks. IEEE Trans. Neural Netw. Learn. Syst. 25(8), 1484–1495 (2014). https://doi.org/10.1109/TNNLS.2013.2294437

    Article  Google Scholar 

  20. de Frutos, J., García-Archilla, B., John, V., Novo, J.: An adaptive SUPG method for evolutionary convection-diffusion equations. Comput. Methods Appl. Mech. Eng. 273, 219–237 (2014). https://doi.org/10.1016/j.cma.2014.01.022

    Article  MathSciNet  MATH  Google Scholar 

  21. Ganesan, S., John, V., Matthies, G., Meesala, R., Abdus, S., Wilbrandt, U.: An object oriented parallel finite element scheme for computations of pdes: design and implementation. In: 2016 IEEE 23rd International Conference on High Performance Computing Workshops (HiPCW) pp. 2–11 (2016). https://doi.org/10.1109/HiPCW.2016.023

  22. Ganesan, S., Srivastava, S.: ALE-SUPG finite element method for convection-diffusion problems in time-dependent domains: conservative form. Appl. Math. Comput. 303, 128–145 (2017). https://doi.org/10.1016/j.amc.2017.01.032

    Article  MathSciNet  MATH  Google Scholar 

  23. Giere, S., Iliescu, T., John, V., Wells, D.: SUPG reduced order models for convection-dominated convection-diffusion-reaction equations. Comput. Methods Appl. Mech. Eng. 289, 454–474 (2015). https://doi.org/10.1016/j.cma.2015.01.020

    Article  MathSciNet  MATH  Google Scholar 

  24. Hecht-Nielsen, R.: Theory of the backpropagation neural network. In: International 1989 joint conference on neural networks, pp. 593–605 vol. 1 (1989)

  25. Roos, H.G., Stynes, M.L.: Numerical Methods for Singularly Perturbed Differential Equations. Springer, Berlin (2008)

    MATH  Google Scholar 

  26. Hornik, K., Stinchcombe, M., White, H.: Multilayer feedforward networks are universal approximators. Neural Netw. 2(5), 359–366 (1989). https://doi.org/10.1016/0893-6080(89)90020-8

    Article  MATH  Google Scholar 

  27. Iooss, B., Lemaître, P.: A review on global sensitivity analysis methods. Oper. Res./Comput. Sci. Interfaces Ser. 59, 101–122 (2015)

    Google Scholar 

  28. Jeon, Y.: Hybridized SUPG and upwind numerical schemes for convection dominated diffusion problems. J. Comput. Appl. Math. 275, 91–99 (2015). https://doi.org/10.1016/j.cam.2014.08.005

    Article  MathSciNet  MATH  Google Scholar 

  29. John, V., Knobloch, P.: On spurious oscillations at layers diminishing (SOLD) methods for convection-diffusion equations: part I—a review. Comput. Methods Appl. Mech. Eng. 196(17–20), 2197–2215 (2007). https://doi.org/10.1016/j.cma.2006.11.013

    Article  MATH  Google Scholar 

  30. John, V., Novo, J.: Error analysis of the SUPG finite element discretization of evolutionary convection-diffusion-reaction equations. SIAM J. Numer. Anal. 49(3), 1149–1176 (2011)

    Article  MathSciNet  Google Scholar 

  31. Johnson, C., Nävert, U., Pitkäranta, J.: Finite element methods for linear hyperbolic problems. Comput. Methods Appl. Mech. Eng. 45(1–3), 285–312 (1984). https://doi.org/10.1016/0045-7825(84)90158-0

    Article  MathSciNet  MATH  Google Scholar 

  32. Kowalski, P.A., Kusy, M.: Determining the significance of features with the use of sobol method in probabilistic neural network classification tasks. In: Proceedings of the 2017 Federated Conference on Computer Science and Information Systems, FedCSIS 2017 11, 39–48 (2017). https://doi.org/10.15439/2017F225

  33. LeVeque, R.J.: Numerical Methods for Conservation Laws. Birkhauser-Verlag, Basel (1990)

    Book  Google Scholar 

  34. Li, R., Wu, Q., Zhu, S.: Proper orthogonal decomposition with SUPG-stabilized isogeometric analysis for reduced order modelling of unsteady convection-dominated convection-diffusion-reaction problems. J. Comput. Phys. 387(18), 280–302 (2019). https://doi.org/10.1016/j.jcp.2019.02.051

    Article  MathSciNet  MATH  Google Scholar 

  35. Lye, K.O., Mishra, S., Ray, D.: Deep learning observables in computational fluid dynamics. J. Comput. Phys. 410, 109339 (2020). https://doi.org/10.1016/j.jcp.2020.109339

    Article  MathSciNet  MATH  Google Scholar 

  36. Nasu, S., Nojima, K., Kawahara, M.: SUPG finite element method for adiabatic flows. Comput. Math. Appl. 66(3), 250–268 (2013). https://doi.org/10.1016/j.camwa.2013.05.003

    Article  MathSciNet  MATH  Google Scholar 

  37. Ray, D., Hesthaven, J.S.: An artificial neural network as a troubled-cell indicator. J. Comput. Phys. 367, 166–191 (2018). https://doi.org/10.1016/j.jcp.2018.04.029

    Article  MathSciNet  MATH  Google Scholar 

  38. Ray, D., Hesthaven, J.S.: Detecting troubled-cells on two-dimensional unstructured grids using a neural network. J. Comput. Phys. 397, 108845 (2019). https://doi.org/10.1016/j.jcp.2019.07.043

    Article  MathSciNet  MATH  Google Scholar 

  39. Codina, R.: Stabilization of incompressibility and convection through orthogonal sub-scales in finite element methods. Comput. Methods Appl. Mech. Eng. 190(13–14), 1579–1599 (2000). https://doi.org/10.1016/S0045-7825(00)00254-1

    Article  MathSciNet  MATH  Google Scholar 

  40. Saltelli, A.: Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 145(2), 280–297 (2002). https://doi.org/10.1016/S0010-4655(02)00280-1

    Article  MathSciNet  MATH  Google Scholar 

  41. Schröder, L., Dimitrov, N.K., Aasted Sorensen, J.: Uncertainty propagation and sensitivity analysis of an artificial neural network used as wind turbine load surrogate model. J. Phys. Conf. Ser. (2020). https://doi.org/10.1088/1742-6596/1618/4/042040

    Article  Google Scholar 

  42. Schulz, E., Speekenbrink, M., Krause, A.: A tutorial on Gaussian process regression: modelling, exploring, and exploiting functions. J. Math. Psychol. 85, 1–16 (2018). https://doi.org/10.1016/j.jmp.2018.03.001

    Article  MathSciNet  MATH  Google Scholar 

  43. Schwander, L., Ray, D., Hesthaven, J.S.: Controlling oscillations in spectral methods by local artificial viscosity governed by neural networks. J. Comput. Phys. 431, 110144 (2021). https://doi.org/10.1016/j.jcp.2021.110144

    Article  MathSciNet  Google Scholar 

  44. Ganesan, S.: An operator-splitting galerkin/supg finite element method for population balance equations: stability and convergence. ESAIM Math. Modell. Numer. Anal. 46(6), 1447–1465 (2012). https://doi.org/10.1051/m2an/2012012

    Article  MathSciNet  MATH  Google Scholar 

  45. Ganesan, S.L.: Stabilization by local projection for convection-diffusion and incompressible flow problems. J. Sci. Comput. 43(3), 326–342 (2010). https://doi.org/10.1007/s10915-008-9259-8

    Article  MathSciNet  MATH  Google Scholar 

  46. Sobol’, I.M.: Sensitivity estimates for non linear mathematical models. Math. Modell. Comput. Exp. 1, 407–414 (1993)

  47. Sobol’, I.M.: Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 55, 271–280 (2001)

  48. Sobol’, I.M., Tarantola, S., Gatelli, D., Kucherenko, S.S., Mauntz, W.: Estimating the approximation error when fixing unessential factors in global sensitivity analysis. Reliab. Eng. Syst. Saf. 92(7), 957–960 (2007). https://doi.org/10.1016/j.ress.2006.07.001

  49. Hughes, T.J.R., Franca, L.P.G.: A new finite element formulation for computational fluid dynamics: Viii. The Galerkin/least-squares method. Comput. Methods Appl. Mech. Eng. 73(2), 173–189 (1989). https://doi.org/10.1016/0045-7825(89)90111-4

    Article  MATH  Google Scholar 

  50. Veiga, M.H., Abgrall, R.: Towards a general stabilisation method for conservation laws using a multilayer perceptron neural network: 1D scalar and system of equations. In: Proceedings of the 6th European Conference on Computational Mechanics: Solids, Structures and Coupled Problems, ECCM 2018 and 7th European Conference on Computational Fluid Dynamics, ECFD 2018, pp. 2525–2539 (2020)

  51. John, V.J.: Error analysis of the supg finite element discretization of evolutionary convection-diffusion-reaction equations. SIAM J. Numer. Anal. 49(3), 1149–1176 (2011). https://doi.org/10.1137/100789002

    Article  MathSciNet  MATH  Google Scholar 

  52. Wang, Z.J., Fidkowski, K., Abgrall, R., Bassi, F., Caraeni, D., Cary, A., Deconinck, H., Hartmann, R., Hillewaert, K., Huynh, H.T., Kroll, N., May, G., Persson, P.O., van Leer, B., Visbal, M.R.: High-order CFD methods: current status and perspective. International Journal for Numerical Methods in Fluids 72(Published online 24 January 2013 in Wiley Online Library (wileyonlinelibrary.com/journal/nmf)), 811–845 (2013). https://doi.org/10.1002/fld.3767

  53. Wilbrandt, U., Bartsch, C., Ahmed, N., Alia, N., Anker, F., Blank, L., Caiazzo, A., Ganesan, S., Giere, S., Matthies, G., Meesala, R., Shamim, A., Venkatesan, J., John, V.: Parmoon—a modernized program package based on mapped finite elements. Comput. Math. Appl. 74, 74–88 (2016). https://doi.org/10.1016/j.camwa.2016.12.020

    Article  MathSciNet  MATH  Google Scholar 

  54. Yadav, S., Ganesan, S.: How deep learning performs with singularly perturbed problems? In: Proceedings—IEEE 2nd International Conference on Artificial Intelligence and Knowledge Engineering, AIKE 2019 pp. 293–297 (2019). https://doi.org/10.1109/AIKE.2019.00058

Download references

Acknowledgements

This work is partially supported by Ministry of Education, Government of India through the scheme for transformational and advanced research in science, MoE/STARS-1/388. Furthermore, S. M. Joshi would like to acknowledge the C. V. Raman PostDoc fellowship from IISc, Bangalore.

Author information

Authors and Affiliations

  1. Department of Computational and Data Sciences, Indian Institute of Science, Bangalore, 560012, India

    Subodh M. Joshi, Thivin Anandh, Bhanu Teja & Sashikumaar Ganesan

Authors
  1. Subodh M. Joshi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Thivin Anandh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Bhanu Teja
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Sashikumaar Ganesan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sashikumaar Ganesan.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A

Appendix A

figure a
figure b
figure c

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Joshi, S.M., Anandh, T., Teja, B. et al. On the choice of hyper-parameters of artificial neural networks for stabilized finite element schemes. Int J Adv Eng Sci Appl Math 13, 278–297 (2021). https://doi.org/10.1007/s12572-021-00306-9

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12572-021-00306-9

Keywords

Mathematics Subject Classification

Search

Navigation