1 Introduction

Global navigation satellite systems (GNSS) are essential for maritime applications. For these applications, GNSS receivers are coupled with inertial measurement units (IMUs), which fuse their respective measurements with the GNSS signal processing algorithms to produce more accurate and reliable positioning results. Information from GNSS units is subsequently integrated with electronic navigation charts (ENCs) and the automatic identification system (AIS), that larger ships are required to carry. Together they form the main positioning, navigation, and timing (PNT) unit necessary for ships of a certain class.

During the last years, studies indicated that the majority of maritime accidents are caused by human error [1]. A case that gathered wide-spread publicity was the sinking of Costa Concordia [2], where the captain misused the ship’s navigation system. A sufficient degree of automation can most likely avoid these kind of accidents. This can be achieved using trustworthy semi-autonomous navigation systems to reduce the effect of human errors. In the light of those studies, the International Maritime Organization (IMO) developed and actively promotes the “e-Navigation” concept [3], which aims for a wider and holistic integration of already existing and new electronic navigational tools to reduce navigation errors and hereby accidents.

One of the key elements of the “e-Navigation” concept is the standardization of GNSS performance requirements with respect to positioning accuracy, integrity and signal availability. Current planning supports the introduction of terrestrial- (differential GNSS) or satellite-based augmentation systems (SBAS), to satisfy the positioning requirements.

Prominent studies [4] indicate that GNSS signals in the maritime environment can be susceptible to severe degradation. The General Lighthouse Authorities of the United Kingdom and Ireland (GLA) in collaboration with the UK Ministry of Defense (MOD) have performed sea-trials with the aim of identifying the effects of GPS jamming on safety and security with respect to navigation at sea [5]. One of the important results of this study was that interference in the GNSS bands not only affects the position outcome of the onboard GNSS receivers. The ship’s digital situation awareness, chart stabilization, digital selective calling and emergency communications could be affected, since they are all coupled and rely on GNSS.

The main and most prevalent reason is degradation due to radio frequency interference (RFI). First, due to the low signal power of GNSS satellite signals at the earth’s surface, the nominal operation of GNSS equipment is easily susceptible to unintentional interference [6]. Emissions of radio systems that either share the same frequency band, e.g. aviation Distance Measurement Equipment (DME) in Galileo E5 band, or operating in the neighboring frequencies and generate harmonics in the GNSS bands, e.g. terminals of Mobile Satellite Systems (MSS) might cause a significant performance degradation or even disable the usage of the GNSS bands.

Additionally, the availability of illegal so-called Personal Privacy Devices (PPDs) has risen over the years. Those type of devices intentionally transmit interfering signals in the GNSS bands. As a result, due to their relative high power in comparison with the GNSS signals, commercial GNSS receivers in a wide radius are jammed and cannot provide navigation information, thus threatening even critical infrastructure [7].

Finally, multipath signal components caused by reflections of the GNSS signals can cause a significant degradation of the positioning accuracy [8]. While that might not be the case in the open sea, vessels preparing for docking in the harbor and traversing in inland waters might experience a significant positioning error, since they have to navigate among tall and metallic structures, that can reflect GNSS signals.

Furthermore, large maritime organizations, such as the Lloyd’s [9] register but also the European Global Navigation Satellite Systems Agency (GSA) [10] state that navigation robustness and cybersecurity will be a major challenge and trend for the upcoming years.

Several single-antenna-based RFI and multipath mitigation techniques for GNSS have been proposed in the literature. The simplest way is to design the antenna, such that it highly attenuates reception from low elevations, since these kinds of interference are expected to impinge from below [11, Chapter 17]. To resolve highly correlated multipath or RFI, rather long observation intervals are necessary if only the time domain is used [12]. Single-antenna approaches show good mitigation capabilities for stationary and none-stationary narrowband interferences in the frequency and time domain [13,14,15]. However, in case of broadband interference, their performance is limited [16].

Antenna arrays allow for mitigation techniques in the spatial domain [17,18,19]. By combining the spatial and time (space-time) domain, the suppression capabilities can be further increased, especially for wide-band and high dynamic interferences [17]. Furthermore, high-resolution parameter estimation algorithms can jointly mitigate multipath and RFI, and provide highly accurate results [20, 21]. This is achieved by separating the LOS component from reflections [20]. However, these methods entail rather high complexity in the parameter estimation as multi-dimensional nonlinear problems have to be solved. Accurate modeling is mandatory.

In radar signal processing, space-time adaptive processing (STAP) techniques are widely known for their mitigation capabilities of clutter [22, 23]. Our approach follows the principles of space-time eigenrake receivers [24], but is tailored to time-delay estimation for GNSS. To mitigate RFI, we combine the blind RFI mitigation technique described in [25] with the adaptive space-time method presented in [26]. Therein, a space-time adaptive principle component analysis (STAPCA) using a compression method based on Canonical Components (CC) with a bank of signal-matched correlators [27] is described. Since the problem is linear and no model-order estimation is required, the computational complexity is significantly reduced. Furthermore, adapted block-wise pre-processing algorithms—Forward–Backward Averaging (FBA) and/or Spatial Smoothing (SPS) [28]—are employed to even increase the decorrelation capabilities.

The remainder of the paper is organized as follows: first, a generic data model including multipath and radio frequency interference is introduced. Based on that, a pre-correlation mitigation technique is described. As a next step, post-correlation mitigation algorithms are motivated and derived. These lead to a description of the time-delay estimation in Sect. 4, followed by a software-based evaluation of the algorithms. Subsequently, the hardware platform used for the experimental proof of concept is described. A summary and conclusion complement the paper.

2 Notation

The following notation is used throughout the paper:

  • \(\mathbf {x}\): bold face lower case letters denote column vectors.

  • \(\mathbf {X}\): bold face capital letters denote matrices.

  • \(\mathrm {Re}\{\cdot \}\text { }(\mathrm {Im}\{\cdot \})\): real (imaginary) part of a complex scalar, vector or matrix.

  • \((\cdot )^T\text { }((\cdot )^H)\): the transpose (hermetian) of a vector or matrix.

  • \(\otimes\): the Kronecker product.

  • \(\Box\): the Khatri–Rao product.

  • \(\mathbf {1}_M\): a column vector of length M consisting of ones.

  • \(\mathbf {I}_Q\): a \(Q\times Q\) identity matrix.

  • \(\text {vec}(\mathbf {X})\): vectorized version of a matrix \(\mathbf {X}\), i.e. all columns of \(\mathbf {X}\) are stacked up.

  • \(\mathrm {E}\left[ \cdot \right]\): the expected value of a random variable, for which ergodicity is always assumed.

  • \(x{[}k{]}=x(kT)\): a sample at index k of a time continuous signal x(t) with sampling period T.

3 Data model

The complex baseband signal with bandwidth B for each satellite, including the line of sight (LOS) and \(L-1\) non-NLOS components, that is received by an antenna array with M antenna elements in the different GNSS frequency bands (e.g. E1/L1, E5/L5) is

$$\begin{aligned} \mathbf {x}(t)=\mathbf {s}(t)+\mathbf {z}(t)+\mathbf {n}(t)= \underbrace{\sum _{\ell =1}^{L}\mathbf {s}_{\ell }(t)}_{\mathbf {s}(t)}+ \underbrace{\sum _{i=1}^{I}\mathbf {z}_{i}(t)}_{\mathbf {z}(t)}+ \mathbf {n}(t), \end{aligned}$$
(1)

where \(\mathbf {s}(t)\) denotes the superimposed signal replicas.

$$\begin{aligned} \mathbf {s}_{\ell }(t)=\mathbf {a}\left( \phi _{\ell },\vartheta _{\ell }\right) \;\gamma _{\ell }\; c(t-\tau _{\ell })\in \;\mathbb {C}^{M\times 1}, \end{aligned}$$
(2)

\(\mathbf {a}\left( \phi _{\ell },\vartheta _{\ell }\right) \in \;\mathbb {C}^{M\times 1}\) defines the steering vector of an antenna array with azimuth angle \(\phi _{\ell }\) and elevation angle \(\vartheta _{\ell }\), \(c(t-\tau _{\ell })\) denotes a periodically repeated pseudo-random (PR) sequence c(t) with time delay \(\tau _{\ell }\), chip duration \(T_c\), and the overall period duration \(T=N_c T_c\) with \(N_c\in \mathbb {N}\). \(\gamma _{\ell }\) is the complex amplitude and \(\mathbf {z}(t)\in \mathbb {C}^{M\times 1}\) denotes superimposed radio interference signals where

$$\begin{aligned} \mathbf {z}_{i}(t)=\mathbf {a}\left( \phi _{i},\vartheta _{i}\right) \; b_i(t), \end{aligned}$$
(3)

and \(b_i(t)\) defines the radio interference signal (i.e. I interference signals). Additionally, we assume temporally and spatially white complex Gaussian noiseFootnote 1\(\mathbf {n}(t)\in \mathbb {C}^{M\times 1}\). In the following, the parameters of the LOS signal have index 1 (i.e. \(\ell =1\)) and the parameters of the NLOS signals (i.e. multipath) with \(\ell =2,\dots ,L\). We define the signal parameter vectors:

$$\begin{aligned} \varvec{\eta }&=[\mathrm {Re}\{\varvec{\gamma }\}^{\mathrm {T}},\mathrm {Im}\{\varvec{\gamma }\}^{\mathrm {T}},\varvec{\phi }^{\mathrm {T}},\varvec{\vartheta }^{\mathrm {T}},\varvec{\tau }^{\mathrm {T}}]^{\mathrm {T}}, \end{aligned}$$
(4)
$$\begin{aligned} \varvec{\eta }_{\ell }&=[\mathrm {Re}\{\gamma _{\ell }\},\mathrm {Im}\{\gamma _{\ell }\},\phi _{\ell },\vartheta _{\ell },\tau _{\ell }]^{\mathrm {T}}, \end{aligned}$$
(5)

with

$$\begin{aligned} \varvec{\gamma }&=[\gamma _1,\dots ,\gamma _L]^{\mathrm {T}},\\ \varvec{\phi }&=[\phi _1,\dots ,\phi _L]^{\mathrm {T}},\\ \varvec{\vartheta }&=[\vartheta _1,\dots ,\vartheta _L]^{\mathrm {T}}\\ \varvec{\tau }&=[\tau _1,\dots ,\tau _L]^{\mathrm {T}}. \end{aligned}$$

The spatial observations for period k of the PRN sequence for N time instances (with a sampling rate of \(T_s\)) read

$$\begin{aligned} \mathbf {x}[(k-1)N+n]=\mathbf {x}(((k-1)N+n)\, T_{s}), \end{aligned}$$

with \(n=1,2,\dots ,N\), \(k=1,2,\dots ,K\), and the sampling frequency \(\frac{1}{T_s}\ge 2B\). The channel parameters are assumed to be constant at least during the k-th period of the observation interval. N and \(T_s\) are chosen s.t. the data contains approximately one code-period (an exact period is not realizable due to the code Doppler). Collecting the samples of the k-th period of the observation interval leads to the following definitions:

$$\begin{aligned} \scriptstyle \mathbf {X}[k] \scriptstyle= & {} \scriptstyle \big [\mathbf {x}[(k-1)N+1], \dots ,\mathbf {x}[(k-1)N+N]\big ]\; \in \; \mathbb {C}^{M \times N}, \end{aligned}$$
(6)
$$\begin{aligned} \scriptstyle \mathbf {N}[k]\scriptstyle= & {} \scriptstyle \big [\mathbf {n}[(k-1)N+1], \dots , \mathbf {n}[(k-1)N+N]\big ]\; \in \; \mathbb {C}^{M \times N}, \end{aligned}$$
(7)
$$\begin{aligned} \scriptstyle \mathbf {S}[k;\varvec{\eta }]\scriptstyle= & {} \scriptstyle \big [\mathbf {s}[(k-1)N+1], \dots , \mathbf {s}[(k-1)N+N]\big ]\; \in \; \mathbb {C}^{M \times N}, \end{aligned}$$
(8)
$$\begin{aligned} \scriptstyle \mathbf {S}_{\ell }[k;\varvec{\eta }_{\ell }]\scriptstyle= & {} \scriptstyle \big [\mathbf {s}_{\ell }[(k-1)N+1], \dots , \mathbf {s}_{\ell }[(k-1)N+N]\big ]\; \in \; \mathbb {C}^{M \times N} \end{aligned}$$
(9)
$$\begin{aligned} \scriptstyle \mathbf {Z}[k]\scriptstyle= & {} \scriptstyle \big [\mathbf {z}[(k-1)N+1], \dots , \mathbf {z}[(k-1)N+N]\big ]\; \in \; \mathbb {C}^{M \times N}, \end{aligned}$$
(10)
$$\begin{aligned} \scriptstyle \mathbf {Z}_{i}[k] \scriptstyle= & {} \scriptstyle \big [\mathbf {z}_{i}[(k-1)N+1], \dots , \mathbf {z}_{i}[(k-1)N+N]\big ]\; \in \; \mathbb {C}^{M \times N}. \end{aligned}$$
(11)

Thus, the signal can be written in matrix notation as

$$\begin{aligned} \mathbf {X}[k]&=\underbrace{\sum _{\ell =1}^{L} \mathbf {S}_{\ell }[k;\varvec{\eta }_{\ell }]}_{\mathbf {S}[k;\varvec{\eta }]}+\underbrace{\sum _{i=1}^{I} \mathbf {Z}_{i}[k]}_{\mathbf {Z}[k]}+\mathbf {N}[k]\nonumber \\&=\mathbf {A}_s[k] \;\mathbf {\Gamma }[k] \;\mathbf {C}[k] +\mathbf {A}_{z}[k]\;\mathbf {B}[k] +\mathbf {N}[k], \end{aligned}$$
(12)

where

$$\begin{aligned} \mathbf {A}_s[k]=[\mathbf {a}(\phi _{1},\vartheta _{1}),\dots ,\mathbf {a}(\phi _{\ell },\vartheta _{\ell }),\dots ,\mathbf {a}(\phi _{L},\vartheta _{L})]\in \mathbb {C}^{M \times L} \end{aligned}$$
(13)

and

$$\begin{aligned} \mathbf {A}_z[k]=[\mathbf {a}(\phi _{1},\vartheta _{1}),\dots , \mathbf {a}(\phi _{i},\vartheta _{i}),\dots , \mathbf {a}(\phi _{I},\vartheta _{I})]\in \mathbb {C}^{M \times I} \end{aligned}$$
(14)

denote the steering matrices for LOS, NLOS, and interference signals.

$$\begin{aligned} \mathbf {\Gamma }[k]:=\mathrm {diag}\{\varvec{\gamma }\}\; \in \mathbb {C}^{L\times L} \end{aligned}$$
(15)

is a diagonal matrix whose entries are complex amplitudes of the signal replicas \(\varvec{\gamma }=[\gamma _1,\dots ,\gamma _{L}]^{\mathrm {T}}\). Furthermore,

$$\begin{aligned} \mathbf {C}[k]=\;[\mathbf {c}[k;\tau _{1}] \cdots \mathbf {c}[k;\tau _{\ell }] \cdots \mathbf {c}[k;\tau _{L}]]^{\mathrm {T}} \in \; \mathbb {R}^{L \times N} \end{aligned}$$
(16)

contains the sampled and shifted c(t) for each impinging wavefront (i.e. the LOS and \(L-1\) NLOS components)

$$\begin{aligned}\mathbf {c}[k;\tau _{\ell }] =[c(((k-1)N+1)T_{s}-\tau _{\ell }), \dots , c(((k-1)N+N)T_{s}-\tau _{\ell })]^{\mathrm {T}}, \end{aligned}$$
(17)

and

$$\begin{aligned} \mathbf {B}[k]=\;[\mathbf {b}_{1}[k] \cdots \mathbf {b}_{i}[k] \cdots \mathbf {b}_{I}[k]]^{\mathrm {T}} \in \; \mathbb {C}^{I \times N} \end{aligned}$$
(18)

contains the sampled \(b_i(t)\) for each of the I interference signals

$$\begin{aligned} \mathbf {b}_{i}[k]= [b_i(((k-1)N+1)T_{s}),\dots , b_i(((k-1)N+n) T_s), \nonumber \\&\dots , b_i(((k-1)N+N) T_{s})]^{\mathrm {T}}. \end{aligned}$$
(19)

The spatial covariance matrix of the received signal, considering the k-th period, can be written as

$$\begin{aligned} \mathbf {R}_{\mathbf {xx}}[k]=\mathrm {E}\left[ \mathbf {x}[(k-1)N+n]\mathbf {x}^{\mathrm {H}}[(k-1)N+n]\right] . \end{aligned}$$
(20)

As we assume that both LOS and NLOS do not correlate with interference and noise, we can write

$$\begin{aligned} \mathbf {R}_{\mathbf {xx}}[k]=\mathbf {R}_{\mathbf {ss}}[k]+\mathbf {R}_{\mathbf {zz}}[k]+\mathbf {R}_{\mathbf {nn}}[k], \end{aligned}$$
(21)

with

$$\begin{aligned} \mathbf {R}_{\mathbf {ss}}[k]= \mathbf {A}_s[k] \mathbf {R}_{\mathbf {s}^{\prime }\mathbf {s}^{\prime }} [k]\mathbf {A}_s^{\mathrm {H}}[k], \end{aligned}$$
(22)
$$\begin{aligned} \mathbf {R}_{\mathbf {zz}}[k]= \mathbf {A}_z[k] \mathbf {R}_{\mathbf {z}^{\prime }\mathbf {z}^{\prime }} [k] \mathbf {A}_z^{\mathrm {H}}[k], \end{aligned}$$
(23)
$$\begin{aligned} \mathbf {R}_{\mathbf {nn}}[k]= \sigma _n^2 \mathbf {I}_M. \end{aligned}$$
(24)

Here, \(\mathbf {R}_{\mathbf {s}^{\prime }\mathbf {s}^{\prime }}[k]\in \mathbb {C}^{L\times L}\) and \(\mathbf {R}_{\mathbf {z}^{\prime }\mathbf {z}^{\prime }}[k]\in \mathbb {C}^{I \times I}\) denote the signal and interference covariance matrix, and \(\mathbf {R}_{\mathbf {nn}}[k]\) denotes the noise covariance matrix.

4 Pre-correlation interference mitigation

In case the power of the signal replicas \(\mathbf {s}_{\ell }(t)\) is much smaller than the power of the noise and the interference (in general about 20–40 dB), the spatial covariance matrix \(\mathbf {R}_{\mathbf {xx}}[k]\) can be approximated by

$$\begin{aligned} \mathbf {R}_{\mathbf {xx}}[k]\approx \mathbf {R}_{\mathbf {zz}}[k]+\mathbf {R}_{\mathbf {nn}}[k]=\mathbf {A}_z[k] \mathbf {R}_{\mathbf {z}^{\prime }\mathbf {z}^{\prime }}[k] \mathbf {A}_z^{\mathrm {H}}[k]+\sigma _n^2 \mathbf {I}_M. \end{aligned}$$
(25)

That means that noise and interference determine the dominant eigenvalues of the correlation matrix in the pre-correlation domain. The goal of the described spatial pre-whitening approach is to spatially uncorrelate and equalize the signal after this procedure. The strongest components are suppressed. This is formally done by performing the following steps (and can be easily seen using an eigenvalue decomposition for \(\mathbf {R}_{\mathbf {xx}}[k]\)):

$$\begin{aligned} \tilde{\mathbf {X}}[k]&= \mathbf {R}_{\mathbf {xx}}^{-\frac{1}{2}}[k]\mathbf {X}[k] \nonumber \\&= \mathbf {R}_{\mathbf {xx}}^{-\frac{1}{2}}[k] \mathbf {A}_s[k] \;\mathbf {\Gamma }[k] \mathbf {C}[k]\nonumber \\&\quad+\mathbf {R}_{\mathbf {xx}}^{-\frac{1}{2}}[k] \mathbf {A}_{z}[k]\;\mathbf {B}[k] +\mathbf {R}_{\mathbf {xx}}^{-\frac{1}{2}}[k]\mathbf {N}[k], \end{aligned}$$
(26)

where the spatial covariance matrix after pre-whitening can be written as

$$\begin{aligned} \mathbf {R}_{\tilde{\mathbf {x}}\tilde{\mathbf {x}}}[k]=\mathbf {R}_{\mathbf {xx}}^{-\frac{1}{2}}[k] \mathbf {R}_{\mathbf {ss}}[k]\mathbf {R}_{\mathbf {xx}}^{-\frac{\mathrm {H}}{2}}[k] +\mathbf {I}_M. \end{aligned}$$
(27)

An estimate for the pre-whitening matrix \(\mathbf {R}_{\mathbf {xx}}^{-\frac{1}{2}}[k]\) is gained by averaging the correlation between the input samples at period k:

$$\begin{aligned} \hat{\mathbf {R}}_{\mathbf {xx}}[k]=\frac{1}{N} \mathbf {X}[k]\mathbf {X}^{\mathrm {H}}[k] \in \mathbb {C}^{M \times M}. \end{aligned}$$
(28)

Since this procedure has to be done continuously for successive periods, an iterative approach allows for an efficient computation of \(\hat{\mathbf {R}}_{\mathbf {xx}}[k]\). The interested reader can find further details in [25, 29].

5 Post-correlation interference and multipath mitigation

The key ingredient for the post-correlation mitigation technique described in the following section is the post-correlation covariance matrix. First, the data model and basic definitions are introduced. This leads to a formal derivation of the covariance matrix. Given certain geometrical properties of the antenna array, the covariance matrix has a special structure, which is described in the next subsection. This enables spatial decorrelation techniques (FBA and SPS). These are presented in the last two subsections.

The following remark about notation and calculus methods used seems necessary: in contrast to the pre-correlation domain, the post-correlation domain has one additional dimension (due to the correlator bank consisting of Q correlators for each satellite channel, which will be described in the following). Naturally, the data could be described using tensors or manifolds. However, this would lay beyond the scope of this work. Therefore, whenever more than two dimensions occur, an “unfolding mechanism” (mainly based on Kronecker products, vectorization and selection matrices) is applied to enable the use of ordinary matrix calculus.

5.1 Post-correlation data model

In this work, we apply a compression (i.e. the reduction of data points using a temporal filter) based on CC (Canonical Components) [21] of a bank of Q signal-matched correlators at the output of each antenna. Thus, the signal at the output of the q-th correlator at each antenna element with \(q = 1,\ldots ,Q\) can be given as

$$\begin{aligned} \mathbf {y}_q[k]= {\tilde{\mathbf {X}}}[k] \frac{1}{N} \mathbf {c}^{*}[k;\kappa _{q}] \in \mathbb {C}^{M \times 1}, \end{aligned}$$
(29)

where \(\kappa _{q}\) denotes the time delay for the correlator tap q. This is basically a sampled version of the correlation with a local replica \(\mathbf {c}\). Again, the sample under consideration has index k. The chip code sequence is assumed to fulfillFootnote 2\(\Vert \mathbf {c}[k;\kappa _{q}]\Vert _2^2\approx N \quad \forall k_q,k\). We define the post-correlation data matrix, which comprises all outputs of each bank of correlators for each of the M antenna elements as

$$\begin{aligned} \mathbf {Y} = {[}\mathbf {y}{[}1{]} \ldots \mathbf {y}{[}K{]} {]}= \scriptstyle \left[ \begin{array}{lcl} \scriptstyle \mathbf {y}_1[1] &{} \scriptstyle \dots &{} \scriptstyle \mathbf {y}_1[K]\\ \scriptstyle &{}\scriptstyle \vdots &{}\scriptstyle \\ \scriptstyle \mathbf {y}_{(M-1)Q}[1] &{} \scriptstyle \dots &{} \scriptstyle \mathbf {y}_{(M-1)Q}[K]\\ \scriptstyle \mathbf {y}_{MQ}[1] &{} \scriptstyle \dots &{} \scriptstyle \mathbf {y}_{MQ}[K]\end{array} \right] \in \mathbb {C}^{MQ \times K}. \end{aligned}$$

In other words, \(\mathbf {Y}\) contains the output for each antenna element and correlators in its columns. Each column includes the outputs for a sample k, where a total of K samples is used. Furthermore, we define

$$\begin{aligned} \scriptstyle \bar{\mathbf {s}}[k] \, = \, & {} \scriptstyle \frac{1}{N}\mathrm {vec}(\mathbf {\Psi }_s[k] \mathbf {\Gamma }[k] \mathbf {C}[k] \mathbf {Q}^{*}[k]) \in \mathbb {C}^{MQ \times 1}, \end{aligned}$$
(30)
$$\begin{aligned} \scriptstyle \bar{\mathbf {n}}[k] \, = \, & {} \scriptstyle \frac{1}{N}\mathrm {vec}({\mathbf {N}}[k] \mathbf {Q}^{*}[k])\in \mathbb {C}^{MQ \times 1}, \end{aligned}$$
(31)
$$\begin{aligned} \scriptstyle \bar{\mathbf {S}}(\varvec{\eta }) \, = \, & {} \scriptstyle \left[ \bar{\mathbf {s}}[1],\dots , \bar{\mathbf {s}}[k], \dots , \bar{\mathbf {s}}[K]\right] \in \mathbb {C}^{MQ \times K}, \end{aligned}$$
(32)
$$\begin{aligned} \scriptstyle \bar{\mathbf {N}} \, = \, & {} \scriptstyle \left[ \bar{\mathbf {n}}[1],\dots , \bar{\mathbf {n}}[k], \dots , \bar{\mathbf {n}}[K]\right] \in \mathbb {C}^{MQ \times K}, \end{aligned}$$
(33)

where

$$\begin{aligned} \mathbf {Q}[k] = \left[ \mathbf {c}[k;\kappa _{1}],\ldots , \mathbf {c}[k;\kappa _{q}],\ldots , \mathbf {c}[k;\kappa _{Q}] \right] \in \mathbb {R}^{N \times Q} \end{aligned}$$
(34)

denotes the reference sequence matrix of the bank of correlators. In other words, \(\mathbf {Q}\) collects the samples of the local replicas in its rows and the time-shifted version for each correlator of the bank in its columns. Finally, the post-correlation data model is given by

$$\begin{aligned} \mathbf {Y}=\bar{\mathbf {S}}(\varvec{\eta })+\bar{\mathbf {N}}. \end{aligned}$$
(35)

Furthermore, we introduce the following short hand notation for the pre-conditioned steering matrices:

$$\begin{aligned} \mathbf {\Psi }_s[k] = \hat{\mathbf {R}}_{\mathbf {xx}}^{-\frac{1}{2}}[k] \mathbf {A}_s[k]. \end{aligned}$$
(36)

5.2 Post-correlation covariance matrix

Consequently, the post-correlation space-time covariance matrix can be given as

$$\begin{aligned} \mathbf {R}_{\mathbf {yy}}=\mathrm {E}\left[ \mathbf {y}[k] \mathbf {y}^{\mathrm {H}}[k]\right] , \end{aligned}$$
(37)

where \(\mathbf {y}[k]\) describes all correlator outputs for the k-th period. With \(\mathrm {E}\left[ \bar{\mathbf {s}}[k] \bar{\mathbf {n}}^{\mathrm {H}}[k]\right] =\mathbf {0}\) we can write

$$\begin{aligned} \mathbf {R}_{\mathbf {y}\mathbf {y}}=\mathbf {R}_{\bar{\mathbf {s}}\bar{\mathbf {s}}}+\mathbf {R}_{\bar{\mathbf {n}}\bar{\mathbf {n}}}, \end{aligned}$$
(38)

with

$$\begin{aligned} \scriptstyle \mathbf {R}_{\bar{\mathbf {s}}\bar{\mathbf {s}}}&\scriptstyle = \, \scriptstyle \mathrm {E}\left[ \bar{\mathbf {s}}[k]\bar{\mathbf {s}}^{\mathrm {H}}[k]\right] \nonumber \\&\scriptstyle = \, \scriptstyle \mathrm {E}\left[ \frac{1}{N^2}\mathrm {vec}(\mathbf {\Psi }_s[k] \mathbf {\Gamma }[k] \mathbf {C}[k] \mathbf {Q}[k]) \mathrm {vec}^{\mathrm {H}}(\mathbf {\Psi }_s[k] \mathbf {\Gamma }[k] \mathbf {C}[k] \mathbf {Q}[k])\right] \nonumber \\&\scriptstyle = \, \scriptstyle \left( \mathbf {I}_Q \otimes \mathbf {\Psi }_s\right) \underbrace{\scriptstyle \frac{1}{N^2}\mathrm {vec}\left( \mathbf {\Gamma }\,\mathbf {C}\,\mathbf {Q}\right) \mathrm {vec}^{\mathrm {H}}\left( \mathbf {\Gamma }\,\mathbf {C}\,\mathbf {Q} \right) }_{:= \, \mathbf {R}_s}\left( \mathbf {I}_Q \otimes \mathbf {\Psi }_s\right) ^{\mathrm {H}},\nonumber \\ \end{aligned}$$
(39)

in case the channel parameters and the time delays of the bank of correlators \(\kappa _q\) are constant within the observation interval of K periods. The noise covariance matrix can be given as

$$\begin{aligned} \mathbf {R}_{\bar{\mathbf {n}}\bar{\mathbf {n}}}=\mathrm {E}\left[ \bar{\mathbf {n}}[k]\bar{\mathbf {n}}^{\mathrm {H}}[k]\right] =\frac{1}{N^2}(\mathbf {G}\otimes \mathbf {I}_M), \end{aligned}$$
(40)

where \(\mathbf {G} = \mathbf {Q}^{\mathrm {T}}\mathbf {Q}^{*}\).

After pre-whitening with \((\mathbf {G}\otimes \mathbf {I}_M)^{-\frac{1}{2}}\) we get

$$\begin{aligned} \tilde{\mathbf {y}}{[}k{]} = (\mathbf {G} \otimes I_M)^{-\frac{1}{2}} \cdot \mathbf {y}{[}k{]} \end{aligned}$$
(41)

with covariance matrix

$$\begin{aligned} \tilde{\mathbf {R}}_{\mathbf {yy}}= & {} \underbrace{(\mathbf {G}\otimes \mathbf {I}_M)^{-\frac{1}{2}}\mathbf {R}_{\bar{\mathbf {s}}\bar{\mathbf {s}}}(\mathbf {G}\otimes \mathbf {I}_M)^{-\frac{\mathrm {H}}{2}}}_{=\left( \mathbf {G}^{-\frac{1}{2}} \otimes \, \mathbf {\Psi }_s\right) \;\mathbf {R}_s\;\left( \mathbf {G}^{-\frac{1}{2}} \otimes \, \mathbf {\Psi }_s\right) ^{\mathrm {H}}}+\frac{1}{N^2}\,\mathbf {I}_{MQ}. \end{aligned}$$
(42)

5.3 Special decorrelation properties

When two or more signals (LOS signal plus several NLOS signals), that are highly correlated or even coherent, are received by the antenna array, the corresponding components in an orthogonal basis (e.g. eigenvectors) of \(\tilde{\mathbf {R}}_{\mathbf {yy}}\) cannot be separated. Thus, a PCA using a corresponding orthogonal basis (e.g. eigen-space ) would fail to separate LOS from NLOS components and to mitigate multipath (NLOS). Techniques such as FBA (forward backward averaging) and Spatial Smoothing (SPS, see [28] for a description of both) can be applied to approximate a decorrelation of the signals and hence to smoothen the corresponding orthogonal basis decomposition (e.g. eigenspace) and to enable a PCA with subsequent precise time-delay estimation of the LOS signal. To apply FBA, the matrix \(\mathbf {\Psi }_s\) must be left centro-hermitianFootnote 3 such that

(43)

A non-left centro hermetian response can be transformed into one via signal adaptive array interpolation (see [30, 31]). It can be shown that if \(\mathbf {A}_s[k]\) and \(\mathbf {A}_z[k]\) are left centro-hermitian and \(\mathbf {R}_{\mathbf {xx}}^{-\frac{1}{2}}[k]\) is centro-hermitianFootnote 4 with

$$\begin{aligned} {\mathbf {R}}_{{\mathbf {xx}}}^{-\frac{1}{2}}[k]= \mathbf {\Pi }_M {\mathbf {R}}_{{\mathbf {xx}}}^{-\frac{*}{2}}[k] \mathbf {\Pi }_M , \end{aligned}$$
(44)

\(\mathbf {\Psi }_s[k]\) is left centro-hermitian as well. In case the interference signals are uncorrleated, \(\mathbf {R}_{\mathbf {zz}}[k]\) is centro-hermitian. \(\mathbf {R}_{\mathbf {xx}}[k]\) is centro-hermitian and based on inversion lemmas \(\mathbf {R}_{\mathbf {xx}}^{-\frac{1}{2}}[k]\) is centro-hermitian as well.

With (43) one can observe from (42) that \(\tilde{\mathbf {R}}_{\mathbf {yy}}\) is block-wise centro-hermitian such that

$$\begin{aligned} \tilde{\mathbf {R}}_{\mathbf {yy}}=\mathbf {\Pi }_{M}^{\otimes }\,\tilde{\mathbf {R}}_{\mathbf {yy}}^{*}\, \mathbf {\Pi }_{M}^{\otimes } \end{aligned}$$
(45)

with

$$\begin{aligned} \mathbf {\Pi }_{M}^{\otimes } = \mathbf {I}_Q \otimes \mathbf {\Pi }_M \in \quad \mathbb {N}^{MQ \times MQ}_0. \end{aligned}$$
(46)

In the following subsections, we describe block-wise space-time FBA for an estimate of the prewhitened space-time covariance matrix \(\hat{\tilde{\mathbf {R}}}_{\mathbf {yy}}\) to decorrelate highly correlated or even coherent signals and to finally perform time-delay estimation of the LOS signal. An estimate of the prewhitened space-time covariance matrix can be given as

$$\begin{aligned} \hat{\tilde{\mathbf {R}}}_{\mathbf {yy}}=(\mathbf {G}\otimes \mathbf {I}_M)^{-\frac{1}{2}}\,\frac{1}{K} \mathbf {Y} \mathbf {Y}^{\mathrm {H}}\,(\mathbf {G}\otimes \mathbf {I}_M)^{-\frac{\mathrm {H}}{2}}. \end{aligned}$$
(47)

5.4 Block-wise forward–backward averaging (FBA)

As the prewhitened space-time covariance matrix has a block-wise centro-hermitian structure, we can apply the following block-wise FBA:

$$\begin{aligned} \hat{\tilde{\mathbf {R}}}_{\mathbf {y}\mathbf {y}}^{\mathrm {FBA}}=\frac{1}{2}\left( \hat{\tilde{\mathbf {R}}}_{\mathbf {y}\mathbf {y}} + \mathbf {\Pi }_{M}^{\otimes }\hat{\tilde{\mathbf {R}}}_{\mathbf {y}\mathbf {y}}^{*}\mathbf {\Pi }_{M}^{\otimes } \right) . \end{aligned}$$
(48)

Because of the Kronecker structure of the extended exchange matrix, the FBA does not depend on the time synchronization between the signal and the bank of correlators. This bock-wise FBA doubles the number of available observations and enables to separate two coherent or highly correlated signals through a decorrelation without decreasing the effective size of the antenna array.

5.5 Block-wise spatial smoothing (SPS)

In the following subsection, we derive a block-wise 2-D SPS scheme for the space-time covariance matrix considering Uniform Rectangular Arrays (URAs) with \(M_x \times M_y\) elements. We define linear subarrays in x- and y-directions with the same number of sensors. Therefore, we get the number of sensors for one subarray in x-direction \(M_{sub_{x}} = M_x - L_x + 1\), where \(L_x\) defines the number of linear subarrays in x-direction. In our case, \(M_{sub_{x}}\) is equal to the number of sensors in y-direction \(M_{sub_{y}}\) and also \(L_x\) is equal to \(L_y\). Then the number of rectangular subarrays is \(L_s = L_x L_y\) and each subarray contains \(M_\mathrm{sub} = M_{sub_{x}}M_{sub_{y}}\) sensor elements.

Since in our case all subarrays have the same size, only the calculations for one direction are needed for the selection matrices:

$$\begin{aligned} \mathbf {J}_{\ell _x} = \left[ \mathbf {0} \; \; \mathbf {I}_{M_{sub_{x}}} \; \;\mathbf {0} \right] \quad \forall \; 1 \le \ell _x \le L_x. \end{aligned}$$
(49)

In case of uniform subarrays \(\mathbf {J}_{\ell _y}\) is equal to \(\mathbf {J}_{\ell _x}\). Then the block-wise 2-D SPS is obtained by a combination of the selection matrices of two different directions. Thus, we get

$$\begin{aligned} \mathbf {J}_{\ell _x,\ell _y}^{\mathrm {Bank}}=\mathbf {I}_Q \otimes \left( \mathbf {J}_{\ell _y} \otimes \mathbf {J}_{\ell _x}\right) \in \mathbb {N}^{QM_\mathrm{sub} \times QM}_0. \end{aligned}$$
(50)

Consequently, the spatially smoothed prewhitened space-time covariance matrix is

$$\begin{aligned} \hat{\tilde{\mathbf {R}}}_{\mathbf {y}\mathbf {y}}^{\mathrm {SPS}} =&\frac{1}{ L_s} \sum _{\ell _y = 1}^{L_y} \sum _{\ell _x = 1}^{L_x} \mathbf {J}_{\ell _x,\ell _y}^{\mathrm {Bank}}\hat{\tilde{\mathbf {R}}}_{\mathbf {y}\mathbf {y}}(\mathbf {J}_{\ell _x,\ell _y} ^{\mathrm {Bank}})^\mathrm {T} \in \mathbb {C}^{QM_\mathrm{sub} \times QM_\mathrm{sub}}. \end{aligned}$$
(51)

Both, block-wise FBA and SPS, can be used separately or in combination to improve the results for the next processing steps.

6 Time-delay estimation

After separating the different signal components in the eigenspace using block-wise FBA, we can use the eigenvector \(\mathbf {w} \in \mathbb {C}^{QM \times 1}\) related to the largest eigenvalueFootnote 5 of \(\hat{\tilde{\mathbf {R}}}_{\mathbf {yy}}^{\mathrm {FBA}+\mathrm {SPS}}\) to estimate the time delay \(\tau _1\) by a spatial filtering of each tap in the compressed time domain and subsequent interpolation. This tap-wise filtering can be written as

$$\begin{aligned} \mathbf {p}[k] =\mathbf {W}^{\mathrm {H}} \mathbf {J}_{1,1}^{\text {Bank}} \left( \mathbf {G}\otimes \mathbf {I}\right) ^{-\frac{1}{2}} \mathbf {y}[k] \quad \in \mathbb {C}^{Q \times 1}, \end{aligned}$$
(52)

where

$$\begin{aligned} \mathbf {W} = \left[ \left( \mathbf {I}_{Q} \otimes \mathbf {1}_{M_{\text {sub}}} \right) \Box \; \mathbf {w}^{\mathrm {T}} \right] ^{\mathrm {T}} \quad \in \mathbb {C}^{QM_{\text {sub}}\times Q}. \end{aligned}$$
(53)

The assumption here is that the contributions to all antenna elements (in terms of amplitude also including the noise) are equal for all elements. The time-delay estimation is equal for all elements (in terms of PRN code delay).

One is interested to find the maximum of the correlation function \(\mathbf {p}[k]\), which may lay in between samples. A spline interpolation yields \(P(\tau )\), which is continuous in its argument (time delay). A line search algorithm is applied to find the maximum of the following optimization problem:

$$\begin{aligned} \hat{\tau }_1=\text {arg } \underset{\tau }{\text {max.}}\quad P(\tau ). \end{aligned}$$
(54)

This time-delay estimate for each satellite serves as the feedback to steer the overall tracking loop—a Delay Locked Loop (DLL). This way, the local replicas of the correlator bank are kept aligned with the received signal and thus enables the extraction of the relevant information (i.e. delay). It also serves as an input for the computation of the navigation solution (position and time).

7 Simulation results

To assess the performance of the RFI and multipath mitigation algorithms introduced in Sects. 3 and 4, the algorithms are applied in two simulated GNSS scenarios. In one scenario, the LOS and multipath signal are spatially uncorrelated, i.e. they impinge from different directions. In the other scenario, the LOS and multipath signal are spatially correlated, i.e. they arrive from a similar direction. For all simulations performed and described in this section, DLR’s software receiver was used. As transmit signal \(c\left( t\right)\), we use the GPS/L1/C/A code [32] of PR sequence 1 with duration \(T_c=997.52\) ns and \(N_{c}=1023\) chips per code period. The receiver uses the outputs of a uniform rectangular array (URA) with \(M_x=M_y=3\), i.e. \(M=9\) antennas with half wavelength spacing and steering vector:

$$\begin{aligned} \mathbf {a}\left( \phi ,\vartheta \right) =\text {vec}\left( \mathbf {a}_x\left( \phi ,\vartheta \right) \otimes \mathbf {a}_y\left( \phi ,\vartheta \right) \right) \end{aligned}$$
(55)

where the x- and y-direction steering vectors are

$$\begin{aligned} \mathbf {a}_x\left( \phi ,\vartheta \right)&=e^{-j\left( \frac{M_x-1}{2}\psi _x\right) }\left[ 1,e^{j\psi _x},\ldots ,e^{j\left( M_x-1\right) \psi _x}\right] \textstyle \in \mathbb {C}^{M\times 1}, \end{aligned}$$
(56)
$$\begin{aligned} \mathbf {a}_y\left( \phi ,\vartheta \right)&=e^{-j\left( \frac{M_y-1}{2}\psi _y\right) }\left[ 1,e^{j\psi _y},\ldots ,e^{j\left( M_y-1\right) \psi _y}\right] \textstyle \in \mathbb {C}^{M\times 1}, \end{aligned}$$
(57)

with

$$\begin{aligned} \psi _x&=\pi \sin \left( \vartheta \right) \cos \left( \phi \right) , \end{aligned}$$
(58)
$$\begin{aligned} \psi _y&=\pi \sin \left( \vartheta \right) \sin \left( \phi \right) . \end{aligned}$$
(59)

The setup for the two scenarios is as follows: during the first 10 s only the LOS component with 46 dB is received. For the next 15 s one additional multipath signal with signal-to-multipath ratio SMR = 6 dB is present. After 25 s w.r.t. to the start of the simulation, the signal is further disturbed by a broadband RFI with interference-to-noise ratio INR = 23 dB. The channel parameters of the scenarios are summarized in Table 1.

Table 1 Parameter setup for the simulations
Full size table

Before describing the simulation results, the following remark is provided: all examples are illustrative and focus only on the parameter variations mentioned before. Signal-to-multipath, signal-to-interference as well as spatial separation would have an effect on pseudorange measurements as well, but are not considered. However, an exhaustive parameter space exploration would lay far beyond the scope of this work.

For comparison, the evaluation includes two single-antenna algorithms. Since the spatial domain is not available, no beamforming or prewithening can be applied. The first algorithm (“MULTI”) has a bank of correlators, while the second one (“Single”) employs a classical receiver structure with three correlators and a non-coherent DLL. All approaches use code-based range measurements only, i.e. no carrier smoothing is implemented. Two multi-antenna algorithms are evaluated as well. They apply pre-whitening for RFI and multi-path mitigation as proposed in Sect. 3. The Space-Time-Principal-Component-Algorithm (STAPCA) uses a bank of correlators and applies the tap-wise filtering explained in Sect. 4. The Principal-Component-Analysis (PCA) algorithm uses only three correlators instead of a correlator bank and, therefore, applies blind beamforming as introduced in [25]. STAPCA uses block-wise and the PCA algorithm FBA and SPS before beamforming with \(L_x=L_y=2\), i.e. \(L_s=4\) subarrays. Table 2 provides an overview of the methods and an explanation of the legend shown in Figs. 1 and 2.

Table 2 Summary of the evaluated algorithms
Full size table

Figure 1 shows the mean squared pseudorange error (time-delay estimate \(\hat{\tau }_1\) multiplied by the speed of light), where each second, a measurement is available. It can be observed, that after 5 s the DLL/PLL for all algorithms are in a steady state. This is the case for all algorithms, meaning the delay estimates are sufficient. After 10 s, the multipath signal is turned on, which leads to a degradation of the pseudorange error estimation performance for all algorithms; however, STAPCA suffers the least, followed by PCA. Both subspace projection methods are able to separate the multipath component and form a spatial zero in its direction.

Fig. 1
figure 1

Pseudorange error for distant LOS and multipath

Full size image

The multicorrelator algorithm using one antenna suppresses the multipath in the temporal domain and has a lower pseudorange error than the traditional approach using only three correlators. The traditional approach, which reflects the state-of-the-art implementation of current commercial maritime GNSS receivers, suffers the most and its pseudorange error grows significantly larger than the rest. After 25 s one RFI signal is also turned on. The single-antenna algorithms loose lock and do not yield a pseudorange estimate. Due to pre-whitening, the multi-antenna algorithms keep their performance after convergence of the tracking loops even when the RFI is turned on.

Figure 2 shows the mean squared pseudorange error for the spatially correlated scenario, i.e. multipath and LOS arrive from a similar direction. Under this type of multipath, the multicorrelator algorithm using a single-antenna algorithm performs comparatively similar w.r.t. the previous scenario producing similar pseudorange error. In contrast, PCA cannot separate the multipath in the spatial domain anymore and thus shows higher pseudorange errors in comparison with the previous scenario. In fact, its performance is comparable to the multicorrelator single-antenna algorithm. However, as STAPCA uses the temporal and spatial domains for signal separation, it still performs significantly better than all other algorithms. Under RFI again only the multi-antenna algorithms keep the lock.

Fig. 2
figure 2

Pseudorange error for close LOS and multipath

Full size image

Surprisingly—in the presence of RFI—the pseudorange error observed for PCA and STAPCA in the analyzed scenario of Fig. 2 is lower than without RFI, i.e. in the time interval from 10 to 25 s. Both subspace projection methods form spatial zeros in the direction of the RFI source. Sidelobes are created as well. This has an effect on the distant multipath component: it is filtered out when the RFI is turned on. However, one cannot generalize based on that specific simulation setup and outcome.

8 Multi-antenna GNSS receiver test platform

The test platform used for the experimental proof of concept (see next section), is described. The mitigation techniques for RFI discussed in Sects. 3 and 4 is implemented in the recording/receiver platform. Such a platform enables the performance validation of the algorithms under realistic conditions, which are typical for maritime applications. Additionally, it allows to compare the different algorithms and settings under reproducible conditions, since the data set is recorded. During the campaign, different experiments with slightly modified setups have been carried out (for repeater/spoofing experiments: see [33]). The platform can be divided into two parts. The first part is used for collecting and storing data sets which are representative for threats in a maritime environment. It has to meet the following qualitative requirements:

  • The power consumption has to be low enough to record long enough.

  • To avoid fire, the heat produced by the devices has to be acceptable.

  • The downmixing has to be done for all channels synchronously in parallel.

  • A calibration signal is necessary to measure and, therefore, compensate different latencies of the cables connecting the antennas, that are in general not equal.

  • All devices (i.e. mixers and AD-samplers) have to be synchronized using a common local oscillator frequency.

  • The sampling rate needs to be high enough to capture the whole GPS L1 band.

  • The storage (i.e. RAID-device) has to be fast and big enough to allow for high bit resolutions of the sampler and several minutes of recording time.

The second part, which is responsible for replaying the data, has to meet the following qualitative requirements:

  • The number of output channels used for replay has to correspond to the number of inputs the (array-based) real-time receiver uses.

  • For post-processing, the IF and the sampling rate of the D/A converters have to be compatible with the receivers that are to be stimulated.

The block diagram of the complete receiver test platform is shown in Fig. 3. The first part of the test platform’s signal processing chain consists of the active antenna array including low-noise amplifiers (LNAs) and RF bandpass filters, as well as the RF front-end with further LNAs, mixers including local oscillators (LO), further amplifiers and finally the streamer with analog to digital (A/D) conversion and data storage.

The sampled and stored data can be used either as an input for a software receiver or as an input stimulus for a real-time receiver. This describes the second part. The number of D/A converters has to be high enough to even stimulate array receivers. The array receiver GALANT is included in the setup. Its purpose in this context is to generate a calibration signal which is (after upmixing to RF) injected into the array directly after the patches. It is recorded in parallel to the GNSS received signal. This allows the calibration of different cable length for post-processing, if this is necessary for certain algorithms not presented in this work (e.g. direction of arrival estimation of the satellite signals).

Fig. 3
figure 3

Blockdiagram of the experimental setup (top) and the post-processing part (bottom)

Full size image

The signal processing chains in the digital domain—for post-processing in software or real-time—can be designed arbitrary in principle. In the context of this work, the processing flow described in the first sections is implemented. The different parts of the platform are described in the following subsections.

8.1 Antenna array

The first element of the receiving chain is an antenna array, providing the necessary degrees of freedom (DOFs) for the mitigation techniques shown in the last sections. The antenna array considered in this campaign was the miniaturized \(2 \times 2\) dual-band (E1 and E5a) array (Fig. 4), composed of stacked microstrip patch antennas, described in [34]. This array enables to fully test the dual-band capability.

Fig. 4
figure 4

A picture of the dual-frequency \(2 \times 2\) antenna array

Full size image

8.2 Front-end

The design of the front-end follows the design as described in [34]. The front-ends are composed of independent channels for the E5a/L5 and E1/L1-bands. Right after both outputs of each array element, directional couplers have been foreseen to couple a calibration signal into the receiver chains. These calibration signals are important for calibrating phase offsets and delay offsets between the different channels of the multi-antenna front-end to enable DOA estimation, beamforming and other array processing algorithms. The down conversion is achieved such that the resulting center frequency after the mixers is 75 MHz for both E5a and E1-bands. This design provides strong robustness to out-of-band RFI while preserving very good signal quality and a low noise figure (NF). In Fig. 5, the hardware implementation of a nine-channel single-frequency front-end is depicted (E1/L1).

Fig. 5
figure 5

A picture of the nine-channel single-frequency RF front-end (for E1/L1)

Full size image

8.3 Sampler

The sampling part is based on the National Instruments (NI) PXI Express System shown in Fig. 6. The processing is configured using LabView and executed on an NI PXIe-8135 Core i7 processor. For A/D conversion the NI PXIe-5171R oscilloscope with eight channels is used. Each channel offers a resolution of 14 bits and a sampling rate of 250 MHz. Additionally, the sampling device includes a field-programmable gate array (FPGA). To reduce the data rate to the required minimum (the bandwidth of the front-end is around 20 MHz), a digital downsampling using bandpass undersampling from 250 MHz to 100 MHz is done. For data storage, a NI HDD-8266 RAID with an overall capacity of 3.5 TB SD drives is connected to the sampling device. The RAID is capable of storing the data stream of all eight A/D channels.

Fig. 6
figure 6

A picture of the NI PXI device used for streaming and replay

Full size image

8.4 Replay

The data replay part is included in the same NI PXI Express System as the streamer. Four NI PXIe-5451 Dual-Channel arbitrary waveform generators are used for D/A conversion and are capable of synchronously replaying stored data of multiple channels at an IF of 75 MHz.

Fig. 7
figure 7

A map showing the location of the jamming testbed

Full size image

9 Experimental evaluation of the test platform

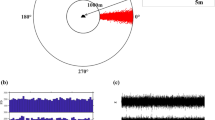
The platform was tested in a maritime measurement campaign in the week from June, 13th to June, 17th 2016, in DLR’s maritime jamming test bed in the Baltic sea, close to Hiddensee, Germany. The location of the test environment is illustrated in Fig. 7 (indicated by the red star). The general setup of all scenarios consists of two vessels. One vessel is equipped with the jammer setup and is anchored at a fixed point. The other vessel is equipped with the first part of the receiver test platform. Different experiments have been performed to demonstrate the mitigation capability for two interference types. Additive white Gaussian noise (AWGN) interference as well as PPDs have been used. To evaluate the algorithms and setup until their limit is reached, an amplifier with a maximum boost of 4 W was necessary.

The receiver vessel (Baltic Taucher II) is shown in Fig. 8. The jamming vessel (Wind Protector)—including the transmission antennae—is shown in Fig. 9.

Fig. 8
figure 8

Receiver installation with the array antenna on the left and the board antenna on the right

Full size image
Fig. 9
figure 9

Jammer installation showing a horn antenna and a small helix antenna

Full size image

9.1 AWGN interference mitigation

The first experimental setup is an AWGN broadband (15 MHz) interference scenario. The vessel, which is equipped with the receiver test platform holds an approximately static position in the main lobe of the interference transmit antenna of the jammer vessel. For the first 30 s of the experiment the interference is turned off. After 30 s the AWGN interference with approximately 20 dB jammer-to-signal ratio (JSR) is turned on. Over 50 s the interference power is continuously increased such that a final JSR of approximately 60 dB is achieved after 80 s.

Figure 10 shows the number of tracked satellites \(N_\text {Sat}\) for the three different receiver setups. The legend in the plots corresponds to the ones described in Table 1 in Sect. 6.

Fig. 10
figure 10

Number of satellites \(N_\text {Sat}\) during the experiment

Full size image

The single-antenna algorithm looses lock to all satellites, right after the interference is turned on. Compared to STAPCA, PCA looses more satellites at a lower JSR and looses lock at approximately 65 s.

Figure 11 shows the mean squared pseudorange residuals (PSR) of all satellites for all three algorithms. It can be observed that in general the STAPCA algorithm shows the lowest PSR with smallest variance in comparison with the other algorithms and is able to track the satellites throughout the whole experiment.

Fig. 11
figure 11

Pseudorange residuals during the experiment

Full size image

Figure 12 shows the scatter plot of the estimated position of the receiver vessel for both PCA and STAPCA. The position estimates have been centered, i.e. the mean position of the whole experiment was subtracted. Since the vessel was not completely static, a slight movement can be recognized. However, a higher variance of the position solution for PCA compared to STAPCA can be observed.

Fig. 12
figure 12

Centered x and y position of the reception antenna in m

Full size image

9.2 PPD interference mitigation

The second experimental setup is a PPD interference scenario. The receiver vessel orthogonally approaches the jamming vessel, as sketched in Fig. 13.

Fig. 13
figure 13

Sketch of the planned dynamic scenario for the PPD setup

Full size image

Based on the measured samples, the SNR was estimated. Since the distance to the interferer decreases, the SNR increases over time, as shown in Fig. 14.

Fig. 14
figure 14

Approximate JSR during the experiment

Full size image

Figure 15 shows the \(\text {C}/\text {N}_0\) values for the PCA and STAPCA algorithm for different satellites. As there is limited GNSS signal multipath, both algorithms have approximately the same \(\text {C}/\text {N}_0\) course for most satellites. However, for PRN 12 and 21 the PCA algorithm has several \(\text {C}/\text {N}_0\) drops during the experiment, which consequently degrades the PVT solution.

Fig. 15
figure 15

\(\text {C}/\text {N}_0\) for different satellites

Full size image

10 Summary and conclusion

In this work, we presented a set of mitigation algorithms for multipath and RFI interference attacks. The techniques are based on antenna arrays. First, a two-stage algorithm for a joint RFI interference and multipath mitigation was presented. It involves a pre-whitening operation, followed either by STAPCA or a multicorrelator approach. Different combinations have been evaluated and compared. This has been done via software simulations using synthetic data and with real data recorded during a measurement campaign carried out at DLR’s maritime jamming testbed in the Baltic sea. The platform used to collect the data has been described as well as basic measurement scenarios with different interference types. STAPCA is able to tolerate more than 55 dB in case of PPD interference and more than 60 dB for AWGN noise-like interference.