A Joint Model Approach for Longitudinal Data with no Time-Zero and Time-to-Event with Competing Risks

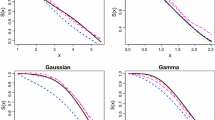
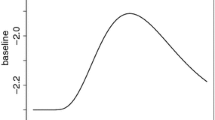
Abstract

The joint modeling of longitudinal and time-to-event data is an active area in biostatistics research. The focus of this article is on developing a modeling framework for these joint models when the longitudinal and time-to-event data do not have a meaningful time-zero. The motivating example is the study of a longitudinal assessment of station during child labor and its relationship to time-to-delivery. A good predictor of delivery type and timing would help obstetricians better manage the end of pregnancy and better facilitate delivery. One measure of labor progression is station, a measure of the position of the fetus’ head in relation to the pelvis of the pregnant women, may be a good marker for delivery time and type. However, women enter the hospital, where their station is closely monitored, at arbitrary points in their labor process, resulting in no clear time zero. In addition, since delivery may be of various types, the competing risks due to type need to be accounted for. We develop a joint model of longitudinal and time-to-event data for this situation. The model is formulated through shared random effects between the survival and longitudinal processes, and parameter estimation is conducted through a Bayesian approach. The model is illustrated with longitudinal data on station where the relationship between station and event-time is studied and the model is used to assess the ability of longitudinal measures of station to predict the type and timing of pregnancy. We illustrate the methodology with longitudinal data taken during labor.