Skip to main content
SpringerLink
Log in

Motor Model-based Optimal Robust Guaranteed Cost Control for Two-motor Web-winding System

  • Regular Papers
  • Intelligent Control and Applications
  • Published:
International Journal of Control, Automation and Systems Aims and scope Submit manuscript

Abstract

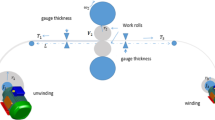
In this paper, a novel comprehensive model for the two-motor web-winding system is proposed, which combines the classical web-winding system model with the driven-motor model. Based on the proposed model, the state feedback robust control (SFRC) strategy is designed to handle systematic uncertainty and time-varying parameters. And then in order to reduce the control cost of the web-winding system, an optimal robust guaranteed cost control (ORGCC) approach is studied. First, the reference control inputs and error dynamic model are derived based on the proposed comprehensive model. Then, the SFRC strategy and ORGCC approach are designed to calculate control compensation. By regarding some suitable parameters as interval variables, the proposed controllers have good robustness for parameter variations and environmental disturbance. Finally, the simulation results illustrate the effectiveness of the proposed model and control.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. H. Hou, X. Nian, H. Xiong, Z. Wang, and Z. Peng, “Robust decentralized coordinated control of a multimotor web-winding system,” IEEE Transactions on Control Systems Technology, vol. 24, no. 4, pp. 1063–6536, July 2016.

    Article  Google Scholar 

  2. Z. Chen, Y. Zheng, T. Zhang, D. S. Wong, and Z. Deng, “Modeling and register control of the speed-up phase in roll-to-roll printing systems,” IEEE Transactions on Automation Science and Engineering, vol. 16, no. 3, pp. 1438–1449, July 2019.

    Article  Google Scholar 

  3. X. Chu, X. Nian, H. Wang, and H. Xiong, “Distributed fault tolerant tracking control for large-scale multi-motor web-winding systems,” IET Control Theory and Applications, vol. 13, no. 4, pp. 543–553, February 2019.

    Article  MathSciNet  MATH  Google Scholar 

  4. D. P. Campbell and T. Teichmann, “Process dynamics: Dynamic behavior of the production process,” Physics Today, vol. 12, no. 6, pp. 46–48, June 1959.

    Article  Google Scholar 

  5. D. King, “The mathematical model of a news paper press,” Newspaper Techniques, vol. 1, pp. 3–7, 1969.

    Google Scholar 

  6. G. Brandenburg, “New mathematical models for web tension and register error,” Proc. of the 3rd International IFAC Conference on Instrumentation and Automation in the Paper, Rubber and Plastics Industries, pp. 411–438, 1976.

  7. D. P. D. Whitworth and M. C. Harrison, “Tension variations in pliable material in production machinery,” Applied Mathematical Modelling, vol. 7, no. 3, pp. 189–196, June 1983.

    Article  Google Scholar 

  8. H. Koc, D. Knittel, M. de Mathelin, and G. Abba, “Modeling and robust control of winding systems for elastic webs,” IEEE Transactions on Control Systems Technology, vol. 10, no. 2, pp. 197–208, March 2002.

    Article  Google Scholar 

  9. P. R. Pagilla, N. B. Siraskar, and R. V. Dwivedula, “Decentralized control of web processing lines,” IEEE Transactions on Control Systems Technology, vol. 15, no. 1, pp. 106–117, January 2007.

    Article  Google Scholar 

  10. J. de J. Rubio, E. Lughofer, J. Pieper, P. Cruz, D. I. Martinez, G. Ochoa, M. A. Islas, and E. Garcia, “Adapting H-infinity controller for the desired reference tracking of the sphere position in the maglev process,” Information Sciences, vol. 569, pp. 669–686, August 2021.

    Article  MathSciNet  Google Scholar 

  11. D. I. Martinez, J. de J. Rubio, V. Garcia, T. M. Vargas, M. A. Islas, J. Pacheco, G. J. Gutierrez, J. A. Mea-Compaña, D. Mujica-Varga, and C. Aguilar-Ibañez, “Transformed structural properties method to determine the controllability and observability of robots,” Applied Sciences, vol. 11, no. 7, p. 3082, January 2021.

    Article  Google Scholar 

  12. L. A. Soriano, E. Zamora, J. M. Vazquez-Nicols, G. Hernández, J. A. B. Madrigal, and D. Balderas, “PD control compensation based on a cascade neural network applied to a robot manipulator,” Frontiers in Neurorobotics, vol. 14, pp. 1–9, December 2020.

    Article  Google Scholar 

  13. D. I. Martinez, J. de J. Rubio, A. Aguilar, J. Pacheco, G. J. Gutierrez, V. Garcia, T. M. Vargas, G. Ochoa, D. R. Cruz, and C. F. Juarez, “Stabilization of two electricity generators,” Complexity, vol. 2020, pp. 1–13, December 2020.

    Article  Google Scholar 

  14. J. R. Garcia-Snchez, S. Tavera-Mosqueda, R. Silva-Ortigoza, V. M. Hemández-Guzm’an, J. Sandoval-Gutiérrez, M. Marcelino-Aranda, H. Taud, and M. Marciano-Melchor, “Robust switched tracking control for wheeled mobile robots considering the actuators and drivers,” Sensors, vol. 18, no. 12, p. 4316, December 2018.

    Article  Google Scholar 

  15. V. Gassmann, D. Knittel, P. R. Pagilla, and M.-A. Bueno, “Fixed-order H∞ tension control in the unwinding section of a web handling system using a pendulum dancer,” IEEE Transactions on Control Systems Technology, vol. 20, no. 1, pp. 173–180, January 2012.

    Google Scholar 

  16. S. H. Jeon, J.-M. Kim, K.-C. Jung, S.-K. Sul, and J. Y. Choi, “Decoupling control of bridle rolls for steel mill drive system,” IEEE Transactions on Industry Applications, vol. 35, no. 1, pp. 119–125, February 1999.

    Article  Google Scholar 

  17. S. Liu, X. Mei, L. Ma, H. You, and Z. Li, “Active disturbance rejection decoupling controller design for roll-to-roll printing machines,” Proc. of IEEE 3rd International Conference on Information Science and Technology (ICIST), pp. 111–116, 2013.

  18. P. R. Raul and P. R. Pagilla, “Design and implementation of adaptive PI control schemes for web tension control in roll-to-roll (R2R) manufacturing,” ISA Transactions, vol. 56, pp. 276–287, May 2015.

    Article  Google Scholar 

  19. F. Janabi-Sharifi, “A neuro-fuzzy system for looper tension control in rolling mills,” Control Engineering Practice, vol. 13, no. 1, pp. 1–13, January 2005.

    Article  Google Scholar 

  20. N. R. Abjadi, J. Soltani, and J. Askari, “Nonlinear sliding-mode control of a multi-motor web-winding system without tension sensor,” Proc. of IEEE International Conference on Industrial Technology, pp. 1–6, 2008.

  21. X. Chu, X. Nian, M. Sun, H. Wang, and H. Xiong, “Robust decentralized fault estimation for loss of actuator effectiveness of multi-motor web-winding system,” International Journal of Control, Automation, and Systems, vol. 17, pp. 691–704, February 2019.

    Article  Google Scholar 

  22. P. R. Raul, S. G. Manyam, P. R. Pagilla, and S. Darbha, “Output regulation of nonlinear systems with application to roll-to-roll manufacturing systems,” IEEE/ASME Transactions on Mechatronics, vol. 20, no. 3, pp. 1089–1098, June 2015.

    Article  Google Scholar 

  23. Q. C. Nguyen, M. Piao, and K. S. Hong, “Multivariable adaptive control of the rewinding process of a roll-to-roll system governed by hyperbolic partial differential equations,” International Journal of Control, Automation, and Systems, vol. 16, pp. 2177–2186, September 2018.

    Article  Google Scholar 

  24. H. Hou, X. Nian, J. Chen, and D. Xiao, “Decentralized coordinated control of elastic web winding systems without tension sensor,” ISA Transactions, vol. 80, pp. 350–359, September 2018.

    Article  Google Scholar 

  25. L. Liu, N. Shao, and M. H. Lin, “Hamilton-based adaptive robust control for the speed and tension system of reversible cold strip rolling mill,” International Journal of Adaptive Control Signal Processing, vol. 33, pp. 626–643, February 2019.

    Article  MathSciNet  MATH  Google Scholar 

  26. X. Niu, C. Zhang, and L. Hui, “Active disturbance attenuation control for permanent magnet synchronous motor via feedback domination and disturbance observer,” IET Control Theory and Applications, vol. 11, no. 6, pp. 807–815, January 2017.

    Article  MathSciNet  Google Scholar 

  27. J. Yang, W. Chen, S. Li, L. Guo, and Y. Yan, “Disturbance/uncertainty estimation and attenuation techniques in PMSM drives: A survey,” IEEE Transactions on Industrial Electronics, vol. 64, no. 4, pp. 3273–3285, April 2017.

    Article  Google Scholar 

  28. F. Claveau, P. Chevrel, and K. Knittel, “A 2DOF gain-scheduled controller design methodology for a multi-motor web transport system,” Control Engineering Practice, vol. 16, no. 5, pp. 609–622, May 2008.

    Article  Google Scholar 

  29. G. Ramrez, R. D. Lorenz, and M. A. Valenzuela, “Observer-based estimation of modulus of elasticity for papermaking process,” IEEE Transactions on Industry Applications, vol. 50, no. 3, pp. 1678–1686, May 2014.

    Article  Google Scholar 

  30. X. Nian, X. Fu, X. Chu, H. Xiong, and H. Wang, “Disturbance observer-based distributed sliding mode control of multimotor web-winding systems,” IET Control Theory and Applications, vol. 14, no. 4, pp. 614–625, January 2020.

    Article  MathSciNet  Google Scholar 

  31. D. Liu, D. Wang, F. Y. Wang, H. Li, and X. Yang, “Neural-network-based online HJB solution for optimal robust guaranteed cost control of continuous-time uncertain nonlinear systems,” IEEE Transactions on Cybernetics, vol. 44, no. 12, pp. 2834–2847, December 2014.

    Article  Google Scholar 

  32. S. Chang and T. Peng, “Adaptive guaranteed cost control of systems with uncertain parameters,” IEEE Transactions on Automatic Control, vol. 17, no. 4, pp. 474–483, August 1972.

    Article  MathSciNet  MATH  Google Scholar 

  33. Z. Xu, X. Nian, H. Wang, and Y. Chen, “Robust guaranteed cost tracking control of quadrotor UAV with uncertainties,” ISA Transactions, vol. 69, pp. 157–165, July 2019.

    Article  Google Scholar 

  34. S. Li, L. Yang, Z. Gao, and K. Li, “Optimal guaranteed cost cruise control for high-speed train movement,” IEEE Transactions on Intelligent Transportation Systems, vol. 17, no. 10, pp. 2879–2887, October 2016.

    Article  Google Scholar 

  35. Y. Zhao and W. Zhang, “Guaranteed cost consensus protocol design for linear multi-agent systems with sampled-data information: An input delay approach,” ISA Transactions, vol. 67, pp. 87–97, March 2017.

    Article  Google Scholar 

  36. I. R. Petersen and D. C. McFarlane, “Optimal guaranteed cost control and filtering for uncertain linear systems,” IEEE Transactions on Automatic Control, vol. 39, no. 9, pp. 1971–1977, September 1994.

    Article  MathSciNet  MATH  Google Scholar 

  37. D. Xu, Q. Wang, and Y. Li, “Optimal guaranteed cost tracking of uncertain nonlinear systems using adaptive dynamic programming with concurrent learning,” International Journal of Control, Automation, and Systems, vol. 18, pp. 1116–1127, May 2020.

    Article  Google Scholar 

  38. J.-G. Lu, Z. Zhu, and Y.-D. Ma, “Robust stability and stabilization of multi-order fractional-order systems with interval uncertainties: An LMI approach,” International Journal of Robust and Nonlinear Control, vol. 31, no. 9, pp. 4081–4099, June 2021.

    Article  MathSciNet  Google Scholar 

  39. H. Xiong, Y. Lv, C. Luo, Y. Gong, and P. Huang, “Motor model-based H∞ robust control for two motor web-winding system,” Proc. of IEEE 2nd China International Youth Conference on Electrical Engineering (CIYCEE), December 2021.

  40. X. Nian and Z. Deng, “Robust synchronization controller design of a two coupling permanent magnet synchronous motors system,” Transactions of the Institute of Measurement and Control, vol. 37, no. 8, pp. 17–24, November 2015.

    Article  Google Scholar 

  41. M. Antivachis, J. A. Anderson, D. Bortis, and J. W. Kolar, “Analysis of a synergetically controlled two-stage three-phase DC/AC buck-boost converter,” CPSS Transactions on Power Electronics and Applications, vol. 5, no. 1, pp. 34–53, March 2020.

    Article  Google Scholar 

  42. L. Liu, Y. Fang, J. Li, and R. Chang, “Modeling and decentralized control for speed and tension multivariable coupling system of reversible cold strip mill,” Control Theory and Applications, vol. 22, no. 2, pp. 529–538, January 2014.

    Google Scholar 

  43. Y. Fang, L. Liu, J. Li, and Y. Xu, “Decoupling control based on terminal sliding mode and wavelet network for the speed and tension system of reversible cold strip rolling mill,” International Journal of Control, vol. 88, no. 8, pp. 1630–1646, January 2015.

    Article  MathSciNet  MATH  Google Scholar 

  44. J. G. Lu and Y. Q. Chen, “Robust stability and stabilization of fractional-order interval systems with the fractional order, α: The 0 ≪ α ≪ 1 case,” IEEE Transactions on Automatic Control, vol. 55, no. 1, pp. 152–158, January 2010.

    Article  MathSciNet  Google Scholar 

  45. W. Mao and J. Chu, “Quadratic stability and stabilization of dynamic interval systems,” IEEE Transactions on Automatic Control, vol. 48, no. 6, pp. 1007–1012, June 2003.

    Article  MathSciNet  MATH  Google Scholar 

  46. H. Hou, X. Nian, S. Xu, M. Sun, and H. Xiong, “Robust decentralized control for large-scale web-winding systems: A linear matrix inequality approach,” Transactions of the Institute of Measurement and Control, vol. 39, no. 7, pp. 953–964, June 2018.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Automation, Central South University, Changsha, 410075, China

    Hongyun Xiong, Yipeng Lv, Bin Cheng & Xiaohong Nian

  2. School of Information Science and Technology, Southwest Jiaotong University, Chengdu, 611756, China

    Xiaoyan Chu

Authors
  1. Hongyun Xiong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yipeng Lv
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Bin Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xiaohong Nian
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Xiaoyan Chu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaohong Nian.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work is supported in part by the National Natural Science Foundation of China under Grant 62173347.

Hongyun Xiong received his M.S. and Ph.D. degrees in mechanical engineering from Xian University of Technology in 1989 and Xian Jiaotong University in 1998, respectively. Currently, he is an associate professor with Central South University, Changsha, China. His main research interests include the modeling, identification, and control of electronic mechanical systems.

Yipeng Lv received his B.S. degree from Central South University in 2020. He is currently working toward an M.S. degree in the School of Automation, Central South University, Changsha, China. His research interests include robust nonlinear control, guaranteed cost control, and data-driven.

Bin Cheng received his B.S. degree from University of South China in 2018. He is currently working toward an M.S. degree in the School of Automation, Central South University, Changsha, China. His research interests include robust nonlinear control and guaranteed cost control.

Xiaohong Nian received his B.S., M.S., and Ph.D. degrees from Northwest Normal University in 1985, Shandong University in 1992, and Peking University in 2004, respectively. Currently, he is a professor with Central South University, Changsha, China. His research interests include control for multi-agent systems and multimotor system.

Xiaoyan Chu received her B.S., M.S., and Ph.D. degrees from Henan Institute of Technology in 2012, Chongqing Jiaotong University in 2015, and Central South University in 2019, respectively. Currently, she is an Assistant Research Fellow with Southwest Jiaotong University, Chengdu, China. Her main research interests include decentralized control, fault diagnosis, and fault tolerant control for multi-motor systems.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xiong, H., Lv, Y., Cheng, B. et al. Motor Model-based Optimal Robust Guaranteed Cost Control for Two-motor Web-winding System. Int. J. Control Autom. Syst. 20, 3808–3821 (2022). https://doi.org/10.1007/s12555-021-0293-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12555-021-0293-8

Keywords

Search

Navigation