Skip to main content
SpringerLink
Log in

Receding Horizon Stability Analysis of Delayed Neural Networks with Randomly Occurring Uncertainties

  • Regular Papers
  • Control Theory and Applications
  • Published:
International Journal of Control, Automation and Systems Aims and scope Submit manuscript

Abstract

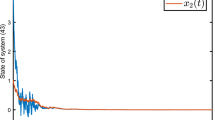
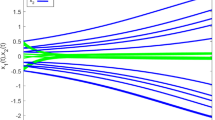
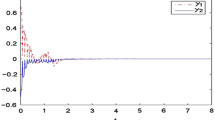
For delayed neural networks with randomly occurring uncertainties (ROU), this paper uses an improved integral inequality to optimize the stability of the receding horizon. The ROU follows some uncorrelated Bernoulli distribution white noise sequence, which it can enter the neural network in a free and random manner. By using a suitable lemma, the ROU problem added in this paper is transformed into a linear matrix inequality. Based on the auxiliary function-based integral inequality method, the new cross terms matrix of linear matrix inequality in the improved Lyapunov-Krasovskii functional is processed. Therefore, some new matrix variables containing more information are generated, so that the results have more degrees of freedom. This paper has obtained the new condition of the end-weighting matrix of the receding horizon cost function, thereby reducing its conservativeness and increasing its upper limit of delay. Finally, the superiority of the method has be illustrated by giving some simulation numerical examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. L. O. Chua and L. Yang, “Cellular neural networks: Applications,” IEEE Transactions on Circuits and Systems, vol. 35, no. 10, pp. 1273–1290, 1988.

    Article  MathSciNet  Google Scholar 

  2. J. Hopfield, “Neurons with grade response have collective computational properties like those of two-state neurons,” Proceedings of the National Academy of Sciences, vol. 81, no. 10, pp. 3088–3092, 1988.

    Article  Google Scholar 

  3. Z. Lin, Y. Xia, P. Shi, and H. Wu, “Robust sliding mode control for uncertain linear discrete systems independent of time-delay,” Int. J. Innov. Comp. Inf. Control, vol. 7, no. 2, pp. 869–880, 2011.

    Google Scholar 

  4. A. N. Michel and D. Liu, Qualitative Analysis and Synthesis of Recurrent Neural Networks, Marcel Dekker, Inc., New York, 2002.

    MATH  Google Scholar 

  5. H. B. Zeng, Y. He, and M. Wu, “Passivity analysis for neural networks with a time-varying delay,” Neurocomputing, vol. 74, no. 5, pp. 730–734, 2011.

    Article  Google Scholar 

  6. Q. Zhou, W. Wang, H. Liang, M. Basin, and B. Wang, “Observer-based event-triggered fuzzy adaptive bipartite containment control of multi-agent systems with input quantization,” IEEE Transactions on Fuzzy Systems, vol. 29, no. 2, pp. 372–384, 2021.

    Article  Google Scholar 

  7. W. Wang, H. J. Liang, Y. N. Pan, and T. S. Li, “Prescribed performance adaptive fuzzy containment control for nonlinear multi-agent systems using disturbance observer,” IEEE Transactions on Cybernetics, vol. 50, no. 9, pp. 3879–3891, 2020.

    Article  Google Scholar 

  8. R. H. Yang, H. Zhang, G. Feng, H. C. Yan, and Z. P. Wang, “Robust cooperative output regulation of multi-agent systems via adaptive event-triggered control,” Automatica, vol. 102, pp. 129–136, 2019.

    Article  MathSciNet  Google Scholar 

  9. Z. C. Li, H. C. Yan, H. Zhang, X. S. Zhan, and C. Z. Huang, “Stability analysis for delayed neural networks via improved auxiliary polynomial-based functions,” IEEE Transactions on Neural Networks and Learning Systems, vol. 30, no. 8, pp. 2562–2568, 2019.

    Article  MathSciNet  Google Scholar 

  10. H. B. Zeng, J. H. Park, and H. Shen, “Robust passivity analysis of neural networks with discrete and distributed delays,” Neurocomputing, vol. 149, pp. 1092–1097, 2015.

    Article  Google Scholar 

  11. Y. Y. Wang, W. X. Zhou, and J. Luo, “Reliable intelligent path following control for a robotic airship against sensor faults,” IEEE-ASME Transactions on Mechatronics, vol. 24, no. 6, pp. 2572–2582, 2019.

    Article  Google Scholar 

  12. Y. Wang, H. Shen, and D. Duan, “On stabilization of quantized sampled-data neural-network-based control systems,” IEEE Transactions on Cybernetics, vol. 47, no. 10, pp. 3124–3135, 2017.

    Article  Google Scholar 

  13. A. Seuret, F. Gouaisbaut, and E. Fridman, “Stability of systems with fast-varying delay using improved Wirtinger’s inequality,” Proc. of IEEE Annual Conference on Decision and Control (CDC), Florence, Italy, DEC 10–13, pp. 946–951, 2013.

  14. K. B. Shi, X. Z. Liu, and Y. Y. Tang, “Some novel approaches on state estimation of delayed neural networks,” Information Sciences, vol. 372, pp. 313–331, 2016.

    Article  Google Scholar 

  15. P. G. Park, J. W. Ko, and C. K. Jeong, “Reciprocally convex approach to stability of systems with time-varying delays,” Automatica, vol. 47, no. 1, pp. 235–238, 2011.

    Article  MathSciNet  Google Scholar 

  16. T. Li, L. Guo, L. Wu, and C. Sun, “Delay-dependent robust stability criteria for delay neural networks with linear fractional uncertainties,” International Journal of Control Automation and Systems, vol. 7, no. 2, pp. 281–287, 2009.

    Article  Google Scholar 

  17. H. B. Zeng, Z. L. Zhai, and Y. He, “New insights on stability of sampled-data systems with time-delay,” Applied Mathematics and Computation, vol. 374, 125041, 2020.

    Article  MathSciNet  Google Scholar 

  18. L. J. Banu and P. Balasubramaniam, “Robust stability analysis for discrete-time neural networks with time-varying leakage delays and random parameter uncertainties,” Neurocomputing, vol. 179, pp. 126–134, 2016.

    Article  Google Scholar 

  19. Z. G. Wu, J. H. Park, and H. Y. Su, “Robust dissipativity analysis of neural networks with time-varying delay and randomly occurring uncertainties,” Nonlinear Dynamics, vol. 69, no. 3, pp. 1323–1332, 2012.

    Article  MathSciNet  Google Scholar 

  20. S. P. Xiao, H. H. Lian, H. B. Zeng, G. Chen, and W. H. Zheng, “Analysis on robust passivity of uncertain neural networks with time-varying delays via free-matrix-based integral inequality,” International Journal of Control Automation and Systems, vol. 15, no. 5, pp. 2385–2394, 2017.

    Article  Google Scholar 

  21. C. K. Ahn and M. T. Lim, “Model predictive stabilizer for T-S fuzzy recurrent multilayer neural network models with general terminal weighting matrix,” Neural Computing and Applications, vol. 23, no. 1, pp. 271–277, 2013.

    Article  Google Scholar 

  22. C. K. Ahn, P. Shi, and L. G. Wu, “Receding horizon stabilization and disturbance attenuation for neural networks with time-varying delay,” IEEE Transactions on Cybernetics, vol. 45, no. 12, pp. 2680–2692, 2015.

    Article  Google Scholar 

  23. B. Yang, M. N. Hao, J. J. Cao, and X. D. Zhao, “Delay-dependent global exponential stability for neural networks with time-varying delay,” Neurocomputing, vol. 338, pp. 172–180, 2019.

    Article  Google Scholar 

  24. K. Gu, J. Chen, and V. L. Kharitonov, Stability of Time-Delay Systems, Media, Springer Science Business, 2003.

    Book  Google Scholar 

  25. C. K. Zhang, Y. He, L. Jiang, W. J. Lin, and M. Wu, “Delay-dependent stability analysis of neural networks with time-varying delay: a generalized free-weighting-matrix approach,” Appl. Math. Comput, vol. 294, pp. 102–120, 2017.

    MathSciNet  MATH  Google Scholar 

  26. H. B. Zeng, Y. He, M. Wu, and J. H. She, “New results on stability analysis for systems with discrete distributed delay,” Automatica, vol. 60, pp. 189–192, 2015.

    Article  MathSciNet  Google Scholar 

  27. X. M. Zhang and Q. L. Han, “New Lyapunov Krasovskii functionals for global asymptotic stability of delayed neural networks,” IEEE Transactions on Neural Networks, vol. 20, no. 3, pp. 533–539, 2009.

    Article  Google Scholar 

  28. L. Xie, “Output feedback H∞ control of systems with parameter uncertainty,” International Journal of Control, vol. 63, pp. 741–750, 1996.

    Article  MathSciNet  Google Scholar 

  29. J. H. Kim, “Further improvement of Jensen inequality and application to stability of time-delayed systems,” Automatica, vol. 64, pp. 121–125, 2016.

    Article  MathSciNet  Google Scholar 

  30. C. K. Ahn and M. T. Lim, “Receding horizon disturbance attenuation for Takagi-Sugeno fuzzy switched dynamic neural networks,” Information Sciences, vol. 280, pp. 53–63, 2014.

    Article  MathSciNet  Google Scholar 

  31. B. Yang, J. Wang, and J. Wang, “Stability analysis of delayed neural networks via a new integral inequality,” Neural Networks, vol. 88, pp. 49–57, 2017.

    Article  Google Scholar 

  32. J. Hu, Z. Wang, H. Gao, and L. K. Stergioulas, “Robust sliding mode control for discrete stochastic systems with mixed time-delays, randomly occurring uncertainties and nonlinearities,” IEEE Transactions on Industrial Electronics, vol. 59, no. 7, pp. 3008–3015, 2012.

    Article  Google Scholar 

  33. H. H. Lian, S. P. Xiao, H. C. Yan, F. W. Yang, and H. B. Zeng, “Dissipativity analysis for neural networks with time-varying delays via a delay-product-type Lyapunov functional approach,” IEEE Transactions on Neural Networks and Learning Systems, vol. 32, no. 3, pp. 975–984, 2021.

    Article  MathSciNet  Google Scholar 

  34. Y. He, M. D. Ji, and C. K. Zhang, “Global exponential stability of neural networks with time-varying delay based on free-matrix-based integral inequality,” Neural Networks, vol. 77, pp. 80–86, 2016.

    Article  Google Scholar 

  35. H. B. Zeng, X. G. Liu, and W. Wang, “A generalized free-matrix-based integral inequality for stability analysis of time-varying delay systems,” Applied Mathematics and Computation, vol. 354, pp. 1–8, 2019.

    Article  MathSciNet  Google Scholar 

  36. W. Wang, H. B. Zeng, and K. L. Teo, “Free-matrix-based time-dependent discontinuous Lyapunov functional for synchronization of delayed neural networks with sampleddata control,” Chinese Physics B, vol. 26, no. 011, pp. 127–134, 2017.

    Google Scholar 

  37. S. P. Xiao, H. H. Lian, H. B. Zeng, G. Chen, and W. H. Zheng, “Analysis on robust passivity of uncertain neural networks with time-varying delays via free-matrix-based integral inequality,” International Journal of Control Automation, vol. 15, no. 5, pp. 2385–2394, 2017.

    Article  Google Scholar 

  38. H. B. Zen, H. C. Li, Y. He, K. L. Teo, and W. Wang, “Hierarchical stability conditions for time-varying delay systems via an extended reciprocally convex quadratic inequality,” Journal of the Franklin Institute, vol. 357, pp. 9930–9941, 2020.

    Article  MathSciNet  Google Scholar 

  39. T. Wang, J. F. Ge, T. Li, X. Chen, and S. M. Fei, “Observer-based H∞ control for synchronization in delayed neural networks under multiple disturbances,” International Journal of Control, Automation and Systems, vol. 18, no. 12, pp. 3121–3132, 2020.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Computer Science and Techology, Tiangong University, Tianjin, 300387, China

    Liankun Sun, Yanyu Wang & Wanru Wang

  2. Tianjin Key Laboratory of Autonomous Intelligence Technology and Systems, Tiangong University, Tianjin, 300387, China

    Liankun Sun & Wanru Wang

Authors
  1. Liankun Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yanyu Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wanru Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yanyu Wang.

Additional information

Publisher’s Note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Project supported by the National Natural Science Foundation of China (Grant nos. 61403278, 61503280). The authors are very indebted to the Editor and the anonymous reviewers for their insightful comments and valuable suggestions that have helped improve the academic research.

Liankun Sun was born in Tianjin, China, in 1979. He received his M. S. degree in control theory and control engineering from Tiangong University, Tianjin, China, in 2005, and a Ph. D. degree in control theory and control engineering from the Tianjin University, Tianjin, China, in 2009. In March 2009, he joined Tiangong University, where he is currently an associate professor. His current research interests include analysis and synthesis of networked control systems, Petri net theory and application, social computing.

Yanyu Wang was born in Hebei Province, China in 1996. She received a bachelor’s degree from the School of Computer Science and Technology, Renai College, Tianjin University, China in 2018. She is currently a graduate student in the School of Computer Science and Technology, Tiangong University. Her main research interests include neural networks, analysis and synthesis of networked control systems.

Wanru Wang received a master’s degree from the Department of Computer, School of Computer and Information Engineering, Tianjin Normal University, China in 2008. She joined Tiangong University in 2001 and she is currently a lecturer in the School of Computer Science and Technology. Her main research interests include networked control and computer applications.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sun, L., Wang, Y. & Wang, W. Receding Horizon Stability Analysis of Delayed Neural Networks with Randomly Occurring Uncertainties. Int. J. Control Autom. Syst. 19, 3297–3308 (2021). https://doi.org/10.1007/s12555-020-0474-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12555-020-0474-x

Keywords

Search

Navigation