Skip to main content
SpringerLink
Log in

Pinning Synchronization of Stochastic T-S Fuzzy Delayed Complex Dynamical Networks with Heterogeneous Impulsive Delays

  • Control Theory and Applications
  • Published:
International Journal of Control, Automation and Systems Aims and scope Submit manuscript

Abstract

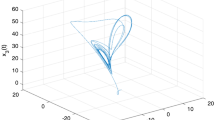
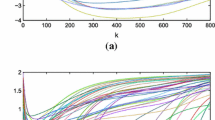
In this paper, we deal with the exponential pinning synchronization (PS) of stochastic T-S fuzzy delayed complex dynamical networks (FDCDNs) with heterogeneous impulsive delays. Unlike the existing works, a fuzzy memory pinning impulsive control (FMPIC) approach is proposed. In order to conquer the difficulties of studying such general system, sufficient conditions that depend on the discrete-delay and distributed-delay impulsive effects are obtained by employing the Lyapunov function, inequality techniques and stochastic analysis theory. It is shown that the PS of FDCDNs can be achieved under the designed FMPIC. Numerical simulation on basis of BA scale-free coupled network is used to illustrate the effectiveness of the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. V. Makarov, S. Kundu, D. Kirsanov, N. Frolov, V. Maksimenko, D. Ghosh, and A. Hramov, “Multiscale interaction promotes chimera states in complex networks,” Communications in Nonlinear Science and Numerical Simulation, vol. 71, pp. 118–129, June 2019.

    Article  MathSciNet  Google Scholar 

  2. Y. Xia, “A new neural network for solving linear programming problems and its application,” IEEE Transactions on Neural Networks, vol. 7, no. 2, pp. 525–529, March 1996.

    Article  Google Scholar 

  3. R. Zhang, D. Zeng, S. Zhong, K. Shi, and J. Cui, “New approach on designing stochastic sampled-data controller for exponential synchronization of chaotic Lur’e systems,” Nonlinear Analysis: Hybrid Systems, vol. 29, pp. 303–321, August 2018.

    MathSciNet  MATH  Google Scholar 

  4. J. Xiao, S. Wen, X. Yang, and S. Zhong, “New approach to global Mittag-Leffler synchronization problem of fractionalorder quaternion-valued BAM neural networks based on a new inequality,” Neural Networks, vol. 122, pp. 320–337, 2020.

    Article  MATH  Google Scholar 

  5. P. Selvaraj, R. Sakthivel, and C. K. Ahn, “Observer-based synchronization of complex dynamical networks under actuator saturation and probabilistic faults,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 49, no. 7, pp. 1516–1526, July 2018.

    Article  Google Scholar 

  6. R. Zhang, D. Zeng, J. H. Park, Y. Liu, and S. Zhong, “Quantized sampled-data control for synchronization of inertial neural networks with heterogeneous time-varying delays,” IEEE Transactions on Neural Networks and Learning Systems, vol. 29, no. 12, pp. 6385–6395, December 2018.

    Article  MathSciNet  Google Scholar 

  7. Y. Shi, J. Cao, and G. Chen, “Exponential stability of complex-valued memristor-based neural networks with time-varying delays,” Applied Mathematics and Computation, vol. 313, pp. 222–234, November 2017.

    Article  MathSciNet  MATH  Google Scholar 

  8. T. Hu, Z. He, X. Zhang, and S. Zhong, “Global synchronization of time-invariant uncertainty fractional-order neural networks with time delay,” Neurocomputing, vol. 339, pp. 45–58, April 2019.

    Article  Google Scholar 

  9. X. Wang, J. H. Park, S. Zhong, and H. Yang, “A switched operation approach to sampled-data control stabilization of fuzzy memristive neural networks with time-varying delay,” IEEE Transactions on Neural Networks and Learning Systems, vol. 31, no. 3, pp. 891–900, 2020.

    Article  MathSciNet  Google Scholar 

  10. L. Li, R. Xu, and J. Lin, “Mean-square stability in lagrange sense for stochastic memristive neural networks with leakage delay,” International Journal of Control, Automation and Systems, vol. 17, no. 8, pp. 2145–2158, May 2019.

    Article  Google Scholar 

  11. J. Luo, W. Tian, S. Zhong, K. Shi, and W. Wang, “Nonfragile asynchronous event-triggered control for uncertain delayed switched neural networks,” Nonlinear Analysis: Hybrid Systems, vol. 29, pp. 54–73, August 2018.

    MathSciNet  MATH  Google Scholar 

  12. W. Xie, H. Zhu, J. Cheng, S. Zhong, and K. Shi, “Finitetime asynchronous H∞ resilient filtering for switched delayed neural networks with memory unideal measurements,” Information Sciences, vol. 487, pp. 156–175, 2019.

    Article  MathSciNet  Google Scholar 

  13. N. Ozcan, M. S. Ali, J. Yogambigai, Q. Zhu, and S. Arik, “Robust synchronization of uncertain Markovian jump complex dynamical networks with time-varying delays and reaction-diffusion terms via sampled-data control,” Journal of the Franklin Institute, vol. 355, no. 3, pp. 1192–1216, February 2018.

    Article  MathSciNet  MATH  Google Scholar 

  14. M. S. Ali and J. Yogambigai, “Extended dissipative synchronization of complex dynamical networks with additive time-varying delay and discrete-time information,” Journal of Computational and Applied Mathematics, vol. 348, pp. 328–341, March 2019.

    Article  MathSciNet  MATH  Google Scholar 

  15. Y. Shan, K. She, S. Zhong, J. Cheng, W. Wang, and C. Zhao, “Event-triggered passive control for Markovian jump discrete-time systems with incomplete transition probability and unreliable channels,” Journal of the Franklin Institute, vol. 356, no. 15, pp. 8093–8117, October 2019.

    Article  MathSciNet  MATH  Google Scholar 

  16. X. Yang, D. W. Ho, J. Lu, and Q. Song, “Finite-time cluster synchronization of T-S fuzzy complex networks with discontinuous subsystems and random coupling delays,” IEEE Transactions on Fuzzy Systems, vol. 23, no. 6, pp. 2302–2316, December 2015.

    Article  Google Scholar 

  17. E. Yucel, M. S. Ali, N. Gunasekaran, and S. Arik, “Sampleddata filtering of Takagi-Sugeno fuzzy neural networks with interval time-varying delays,” Fuzzy Sets and Systems, vol. 316, pp. 69–81, June 2017.

    Article  MathSciNet  MATH  Google Scholar 

  18. R. Rakkiyappan, A. Chandrasekar, and S. Lakshmanan, “Stochastic sampled data robust stabilisation of TS fuzzy neutral systems with randomly occurring uncertainties and time-varying delays,” International Journal of Systems Science, vol. 47, no. 10, pp. 2247–2263, November 2016.

    Article  MathSciNet  MATH  Google Scholar 

  19. X. Wang, J. H. Park, G. Zhao, and S. Zhong, “An improved fuzzy sampled-data control to stabilization of T-S fuzzy systems with state delays,” IEEE Transactions on Cybernetics, 2019. DOI: 10.1109/TCYB.2019.2910520

    Google Scholar 

  20. K. Shi, J. Wang, Y. Tang, and S. Zhong, “Reliable asynchronous sampled-data filtering of T-S fuzzy uncertain delayed neural networks with stochastic switched topologies,” Fuzzy Sets and Systems, vol. 381, pp. 1–25, 2020.

    Article  MathSciNet  Google Scholar 

  21. R. Saravanakumar, M. S. Ali, H. Huang, J. Cao, and Y. H. Joo, “Robust H∞ state-feedback control for nonlinear uncertain systems with mixed time-varying delays,” International Journal of Control, Automation and Systems, vol. 16, no. 1, pp. 225–233, March 2018.

    Article  Google Scholar 

  22. X. Yang, J. Cao, and J. Lu, “Synchronization of delayed complex dynamical networks with impulsive and stochastic effects,” Nonlinear Analysis: Real World Applications, vol. 12, no. 4, pp. 2252–2266, August 2011.

    Article  MathSciNet  MATH  Google Scholar 

  23. W. Xie, H. Zhu, S. Zhong, D. Zhang, K. Shi, and J. Cheng, “Extended dissipative estimator design for uncertain switched delayed neural networks via a novel triple integral inequality,” Applied Mathematics and Computation, vol. 335, pp. 82–102, October 2018.

    Article  MathSciNet  MATH  Google Scholar 

  24. Y. Feng, “Fuzzy stochastic differential systems,” Fuzzy Sets and Systems, vol. 115, no. 3, pp. 351–363, November 2000.

    Article  MathSciNet  MATH  Google Scholar 

  25. R. Sakthivel, T. Saravanakumar, Y. K. Ma, and S. M. Anthoni, “Finit-time resilient reliable sampled-data control for fuzzy systems with randomly occurring uncertainties,” Fuzzy Sets and Systems, vol. 329, pp. 1–18, 2017.

    Article  MathSciNet  MATH  Google Scholar 

  26. Y. Tang, J. A. Fang, M. Xia, and X. Gu, “Synchronization of Takagi-Sugeno fuzzy stochastic discrete-time complex networks with mixed time-varying delays,” Applied Mathematical Modelling, vol. 34, no. 4, pp. 843–855, April 2010.

    Article  MathSciNet  MATH  Google Scholar 

  27. M. Syed Ali, M. Usha, J. Cao, and G. Lu, “Synchronisation analysis for stochastic T-S fuzzy complex networks with coupling delay,” International Journal of Systems Science, vol. 50, no. 3, pp. 585–598, January 2019.

    Article  MathSciNet  Google Scholar 

  28. H. Yang, L. Shu, X. Wang, and S. Zhong, “Synchronization of IT2 stochastic fuzzy complex dynamical networks with time-varying delay via fuzzy pinning control,” Journal of the Franklin Institute, vol. 356, no. 3, pp. 1484–1501, February 2019.

    Article  MathSciNet  MATH  Google Scholar 

  29. X. Wang, J. H. Park, K. She, S. Zhong, and L. Shi, “Stabilization of chaotic systems with T-S fuzzy model and nonuniform sampling: a switched fuzzy control approach,” IEEE Transactions on Fuzzy Systems, vol. 27, no. 6, pp. 1263–1271, June 2019.

    Article  Google Scholar 

  30. Z. Yang and D. Xu, “Stability analysis and design of impulsive control systems with time delay,” IEEE Transactions on Automatic Control, vol. 52, no. 8, pp. 1448–1454, 2007.

    Article  MathSciNet  MATH  Google Scholar 

  31. X. Yang and Z. Yang, “Synchronization of T-S fuzzy complex dynamical networks with time-varying impulsive delays and stochastic effects,” Fuzzy Sets and Systems, vol. 235, pp. 25–43, January 2014.

    Article  MathSciNet  MATH  Google Scholar 

  32. Z. Wu, D. Liu, and Q. Ye, “Pinning impulsive synchronization of complex-variable dynamical network,” Communications in Nonlinear Science and Numerical Simulation, vol. 20, no. 1, pp. 273–280, January 2015.

    Article  MathSciNet  MATH  Google Scholar 

  33. W. He, F. Qian, and J. Cao, “Pinning-controlled synchronization of delayed neural networks with distributed-delay coupling via impulsive control,” Neural Networks, vol. 85, pp. 1–9, January 2017.

    Article  MATH  Google Scholar 

  34. X. Wang, X. Liu, K. She, and S. Zhong, “Pinning impulsive synchronization of complex dynamical networks with various time-varying delay sizes,” Nonlinear Analysis: Hybrid Systems, vol. 26, pp. 307–318, November 2017.

    MathSciNet  MATH  Google Scholar 

  35. X. Lu, X. Zhang, and Q. Liu, “Finite-time synchronization of nonlinear complex dynamical networks on time scales via pinning impulsive control,” Neurocomputing, vol. 275, pp. 2104–2110, January 2018.

    Article  Google Scholar 

  36. Z. Wu, G. Chen, and X. Fu, “Outer synchronization of drive-response dynamical networks via adaptive impulsive pinning control,” Journal of the Franklin Institute, vol. 352, no. 10, pp. 4297–4308, October 2015.

    Article  MathSciNet  MATH  Google Scholar 

  37. Q. Fu, J. Cai, S. Zhong, and Y. Yu, “Pinning impulsive synchronization of stochastic memristor-based neural networks with time-varying delays,” International Journal of Control, Automation and Systems, vol. 17, no. 1, pp. 243–252, January 2019.

    Article  Google Scholar 

  38. X. Liu, K. Zhang, and W. C. Xie, “Stabilization of timedelay neural networks via delayed pinning impulses,” Chaos, Solitons & Fractals, vol. 93, pp. 223–234, 2016.

    Article  MathSciNet  Google Scholar 

  39. H. Yang, X. Wang, S. Zhong, and L. Shu, “Synchronization of nonlinear complex dynamical systems via delayed impulsive distributed control,” Applied Mathematics and Computation, vol. 320, pp. 75–85, March 2018.

    Article  MathSciNet  MATH  Google Scholar 

  40. X. Wang, X. Liu, K. She, S. Zhong, and L. Shi, “Delaydependent impulsive distributed synchronization of stochastic complex dynamical networks with time-varying delays,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 49, no. 7, pp. 1496–1504, July 2019.

    Article  Google Scholar 

  41. W. Hu and Q. Zhu, “Stability criteria for impulsive stochastic functional differential systems with distributeddelay dependent impulsive effects,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019. DOI: 10.1109/TSMC.2019.2905007

    Google Scholar 

  42. X. Liu, K. Zhang, “Stabilization of nonlinear time-delay systems: Distributed-delay dependent impulsive control,” Systems & Control Letters, vol. 120, pp. 17–22, 2018.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Southwest University, Chongqing, 400715, China

    Huilan Yang & Tao Zhan

  2. School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu Sichuan, 611731, China

    Lan Shu & Shouming Zhong

  3. College of Electronic and Information Engineering, Southwest University, Chongqing, 400715, China

    Xin Wang

Authors
  1. Huilan Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lan Shu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shouming Zhong
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Tao Zhan
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Xin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xin Wang.

Additional information

Publisher’s Note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Recommended by Associate Editor Choon Ki Ahn under the direction of Editor Euntai Kim. This research was supported in part by the National Natural Science Foundation of China (Grant. 61903310 and Grant. 61771004), and in part by the Fundamental Research Funds for the Central Universities (Grant. SWU119025 and Grant. SWU119023).

Huilan Yang received her Ph.D. degree in mathematics from the School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu, China, in 2018. She joined the School of Mathematics and Statistics, Southwest University, Chongqing, China, in 2019. Her current research interests include T-S fuzzy systems, neural networks and complex dynamical networks.

Lan Shu received her B.A. (in applied mathematics) and M.S. degrees (in Communication and System) from the University of Electronic Science and Technology of China (UESTC), in 1984 and 1987, respectively. In 2004, she studied in University of Victoria of Australia. Currently, she is a Professor of School of Mathematical Sciences, UESTC, Chengdu, China. She is the author or co-author of more than 100 journal papers, one book, including 30 papers collected by SCI, EI, and ISTP. Her current interests involve fuzzy mathematics theory and application, rough set theory and application, and automata theory and application.

Shouming Zhong received his B.S. degree in Applied Mathematics on differential equation from University of Electronic Science and Technology of China, Chengdu, China, in 1982. He has been a Professor with the School of Mathematical Sciences, University of Electronic Science and Technology of China, since 1997. His research interests include stability theorem and its application research of the differential system, robustness control, neural network and biomathematics.

Tao Zhan received her Ph.D. degree in School of Mathematics, Shandong University, Jinan, China, in 2019. From 2017 to 2018, she was an exchange Ph.D. student in Department of Applied Mathematics, University of Waterloo, Canada. She is currently a Lecturer in School of Mathematics and Statistics, Southwest University, Chongqing, China. Her research interests include nonlinear fractional order systems, singular system, impulsive control, and stability analysis.

Xin Wang received his Ph.D. degree in software engineering from the School of Information and Software Engineering, University of Electronic Science and Technology of China, Chengdu, China, in 2018. He joined the College of Electronic and Information Engineering, Southwest University, Chongqing, in 2019. His current research interests include hybrid systems and control, T-S fuzzy systems, synchronization of complex networks and their various applications.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, H., Shu, L., Zhong, S. et al. Pinning Synchronization of Stochastic T-S Fuzzy Delayed Complex Dynamical Networks with Heterogeneous Impulsive Delays. Int. J. Control Autom. Syst. 18, 2599–2608 (2020). https://doi.org/10.1007/s12555-019-0808-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12555-019-0808-8

Keywords

Search

Navigation