Skip to main content
SpringerLink
Log in

Fuzzy Control with Pole Assignment and Variance Constraints for Continuous-time Perturbed Takagi-Sugeno Fuzzy Models: Application to Ship Steering Systems

  • Intelligent Control and Applications
  • Published:
International Journal of Control, Automation and Systems Aims and scope Submit manuscript

Abstract

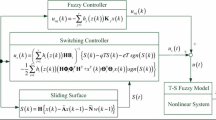
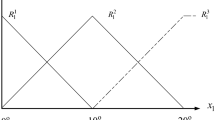
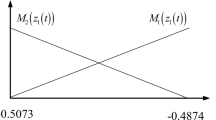
The stability analysis and controller design of stochastic systems have become much more important because the stochastic behaviors usually exist in practical nonlinear systems. In this paper, a robust fuzzy controller design approach is proposed with multiple constraints, including state variance constraints, output variance constraints, and pole placement constraints. At first, nonlinear systems are expressed as the Takagi-Sugeno fuzzy model, and the parallel distributed compensation method is applied to design the robust fuzzy controllers. Next, considering the stability analysis and the performance constraints of perturbed Takagi-Sugeno fuzzy models, Lyapunov conditions are developed based on covariance control theory, pole placement theory and robust control theory. By constructing the stability conditions with multiple constraints, the proposed fuzzy control problem can be effectively transferred into the linear matrix inequality problem. It can be solved by the convex optimal programming algorithm. At last, a nonlinear ship steering system is selected to verify the effectiveness and applicability of the proposed robust fuzzy controller design method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. T. Takagi and M. Sugeno, “Fuzzy identification of systems and its applications to modeling and control,” IEEE Transactions on Systems, Man, Cybernetics, vol. 15, no. 1, pp. 116–132, 1985.

    Article  Google Scholar 

  2. B. Wang, J. Y. Xue, F. J. Wu, and D. L. Zhu, “Robust Takagi-Sugeno fuzzy control for fractional order hydro-turbine governing system,” ISA Transactions, vol. 65, pp. 72–80, 2016.

    Article  Google Scholar 

  3. W. J. Chang, F. L. Hsu, and C. C. Ku, “Complex performance control using sliding mode fuzzy approach for discrete-time nonlinear systems via T-S fuzzy model with bilinear consequent part,” International Journal of Control, Automation and Systems, vol. 15, no. 4, pp. 1901–1915, 2017.

    Article  Google Scholar 

  4. X. H. Chang and Y. M. Wamg, “Peak-to-peak filtering for networked nonlinear DC motor systems with quantization,” IEEE Transactions on Industrial Informatics, vol. 14, no. 12, pp. 5378–5388, 2018.

    Article  Google Scholar 

  5. S. Adbelmalek, A. T. Azar, and D. Dib, “A novel actuator fault-tolerant control strategy of DFIG-based wind turbines using Takagi-Sugeno multiple models,” International Journal of Control, Automation and Systems, vol. 16, no. 3, pp. 1415–1424,2018.

    Article  Google Scholar 

  6. J. Dong and G. H. Yang, “Reliable state feedback control of T-S fuzzy systems with sensor faults,” IEEE Transactions on Fuzzy Systems, vol. 23, no. 2, pp. 421–433, 2015.

    Article  Google Scholar 

  7. J. Dong, Y. Wu, and G. H. Yang, “A new sensor fault isolation method for T-S fuzzy systems,” IEEE Transactions on Cybernectics, vol. 47, no. 9, pp. 2437–2447, 2017.

    Article  Google Scholar 

  8. X. H. Chang and G. H. Yang, “Nonfragile filtering of continuous-time fuzzy systems,” IEEE Transactions on Signal Processing, vol. 59, no. 4, pp. 1528–1538, 2011.

    Article  MathSciNet  Google Scholar 

  9. S. H. Guo, F. L. Zhu, and L. Y. Xu, “Unknown input observer design for Takagi-Sugeno fuzzy stochastic system,” International Journal of Control, Automation and Systems, vol. 13, no. 4, pp. 1003–1009, 2015.

    Article  Google Scholar 

  10. X. H. Chang, J. H. Park, and P. Shi, “Fuzzy resilient energy-to-peak filtering for continuous-time nonlinear systems,” IEEE Transactions on Fuzzy Systems, vol. 25, no. 6, pp. 1576–1588, 2017.

    Article  Google Scholar 

  11. Y. Cui, Y. L. Liu, W. B. Zhang, and F. E. Alsaadi, “Stochastic stability for a class of discrete-time switched neural networks with stochastic noise and time-varying mixed delays,” International Journal of Control, Automation and Systems, vol. 16, no. 1, pp. 158–167, 2018.

    Article  Google Scholar 

  12. A. Hotz and R. E. Skelton, “Covariance control theory,” International Journal of Control, vol. 46, no. 1, pp. 13–32, 1987.

    Article  MathSciNet  Google Scholar 

  13. E. Collins and R. E. Skelton, “A theory of state covariance assignment for discrete systems,” IEEE Transactions on Automatic Control, vol. 32, no. 1, pp. 35–41, 1987.

    Article  MathSciNet  Google Scholar 

  14. W. J. Chag, W. H. Huang, and C. C. Ku, “Robustfuzzy control for discrete perturbed time-delay affine Takagi-Sugeno fuzzy models,” International Journal of Control, Automation and Systems, vol. 9, no. 1, pp. 86–97, 2011.

    Article  Google Scholar 

  15. Y L. Zhuo, M. Chen, and C. S. Jiang, “Robust tracking control of perturbed MIMO nonlinear systems with application to UAVs,” IEEE/CAA Journal of Automatica Sinica, vol. 2, no. 1, pp. 25–32, 2015.

    Article  MathSciNet  Google Scholar 

  16. C. L. Zhang, J. X. Wang, S. H. Li, B. Wu, and C. J. Qian, “Robust control for PWM-based DC-DC buck power converters with perturbedty via sampled-data output feedback,” IEEE Transactions on Power Electronics, vol. 30, no. l,pp. 504–515, 2015.

    Article  Google Scholar 

  17. W. J. Chang, C. C. Ku, and P. H. Huang, “Robust fuzzy control for perturbed stochastic time-delay TakagiSugeno fuzzy models for achieving passivity,” Fuzzy Set and Systems, vol. 161, no. 15, pp. 2012–2032, 2010.

    Article  Google Scholar 

  18. W. J. Chang and S. M. Wu, “Input and state constrained fuzzy controller design for ship steering systems with structured perturbations,” IEEE/ASME International Conference on Advanced Intelligent Mechatronics, vol. 1, pp. 564–569, 2003.

    Google Scholar 

  19. W. J. Chang and B. Y. Huang, “Robust fuzzy control subject to state variance and passivity constraints for perturbed nonlinear systems with multiplicative noises,” ISA Transactions, vol. 53, no. 6, pp. 1787–1795, 2014.

    Article  Google Scholar 

  20. A. Cherifi, K. Guelton, and L. Arcese, “Quadratic design of robust controllers for perturbed T-S models with D-stability constraints,” IFAC-PapersOnLine, vol. 49, no. 5, pp. 19–24, 2016.

    Article  MathSciNet  Google Scholar 

  21. W. J. Chang, C. C. Ku, and Q. H. Yu, “Sliding mode fuzzy control for nonlinear stochastic systems subject to pole assignment and variance constraint,” Information Sciences, vol. 432, pp. 133–145, 2018.

    Article  MathSciNet  Google Scholar 

  22. W. J. Chang, C. C. Ku, and Q. H. Yu, “Robust sliding mode fuzzy control for perturbed nonlinear stochastic systems subject to input and state requirements,” Journal of Intelligent & Fuzzy Systems, vol. 32, no. 6, pp. 4285–4297, 2017.

    Article  Google Scholar 

  23. D. S. Bernstein and W. M. Haddad, “Robust stability and performance analysis for linear dynamic systems,” IEEE Transactions on Automatic Control, vol. 34, no. 7, pp. 751–758, 1989.

    Article  MathSciNet  Google Scholar 

  24. J. H. Xu, R. E. Skelton, and G. Zhu, “Upper and lower co-variance bounds for perturbed linear systems,” IEEE Transactions on Automatic Control, vol. 35, no. 8, pp. 944–948, 1990.

    Article  MathSciNet  Google Scholar 

  25. W. J. Chang and S. M. Wu, “Continuous fuzzy controller design subject to minimizing control input energy with output variance constraints,” European Journal of Control, vol. 11, no. 3, pp. 269–277, 2005.

    Article  MathSciNet  Google Scholar 

  26. M. Liu, L. X. Zhang, P. Shi, and H. R. Karimi, “Robust control of stochastic systems against bounded disturbances with application to flight control,” IEEE Transactions on Industrial Electronics, vol. 6, no. 3, pp. 1504–1515, 2014.

    Article  Google Scholar 

  27. B. P. G. V. Parys, D. Kuhn, P. G. Goulart, and M. Morari, “Distributionally robust control of constrained stochastic systems,” IEEE Transactions on Automatic Control, vol. 6, no. 2, pp. 430–442, 2016.

    MathSciNet  MATH  Google Scholar 

  28. W. J. Chang, L. Z. Liu, and C. C. Ku, “Passive fuzzy controller design via observer feedback for stochastic Takagi-Sugeno fuzzy models with multiplicative noises,” International Journal of Control, Automation and Systems, vol. 9, no. 3, pp. 550–557, 2011.

    Article  Google Scholar 

  29. W. J. Chang, P. H. Chen, and C. C. Ku, “Variance and passivity constrained sliding mode fuzzy control for continuous stochastic non-linear systems,” Neurocomputing, vol. 201, pp. 29–39, 2016.

    Article  Google Scholar 

  30. M. Chilali and P. Gahinet, “Design with pole placement constraints: an LMI approach,” IEEE Transactions on Automatic Control, vol. 41, no. 3, pp. 358–367, 1996.

    Article  MathSciNet  Google Scholar 

  31. M. Chilali, P. Gahinet, and P. Apkarian, “Robust pole placement in LMI regions,” IEEE Transactions on Automatic Control, vol. 44, no. 12, pp. 2257–2270, 1999.

    Article  MathSciNet  Google Scholar 

  32. F. B. Li, P. Shi, L. G. Wu, and X. Zhang, “Fuzzy-model-based D-stability and nonfragile control for discrete-time descriptor systems with multiple delays,” IEEE Transactions on Fuzzy Systems, vol. 22, no. 4, pp. 1019–1025, 2014.

    Article  Google Scholar 

  33. Y B. Gao, H. Y. Li, L. G. Wu, H. R. Karimi, and H. K. Lam, “Optimal control of discrete-time interval type-2 fuzzy-model-based systems with D-stability constraint and control,” Signal Processing, vol. 120, pp. 406–421, 2016.

    Article  Google Scholar 

  34. P. -F. Toulotte, S. Delprat, T. -M. Guerra, and J. Boonaert, “Vehicle spacing control using robust fuzzy control with pole placement in LMI region,” Engineering Applications of Artificial Intelligence, vol. 21, no. 5, pp. 756–768, 2008.

    Article  Google Scholar 

  35. A. H. Besheer, H. M. Emara, and M. M. Abdel Aziz, “Wind energy conversion system regulation via LMI fuzzy pole cluster approach,” Electric Power Systems Research, vol. 79, no. 4, pp. 531–538, 2009.

    Article  Google Scholar 

  36. K. Tanaka and M. Sugeno, “Stability analysis and design of fuzzy control systems,” Fuzzy Set and Systems, vol. 45, no. 2, pp. 135–156, 1992.

    Article  MathSciNet  Google Scholar 

  37. H. O. Wang, K. Tanaka, and M. F. Griffin, “Parallel distributed compensation of nonlinear systems by Takagi-Sugeno fuzzy model,” Proc. of The Fourth IEEE International Conference and the Second International Fuzzy Engineering Symposium on Fuzzy Systems, vol. 2, pp. 531–538, 1995.

    Google Scholar 

  38. W. J. Chang and S. M. Wu, “Fuzzy control with input energy and state variance constraints for perturbed ship steering systems,” International Journal of Computer Applications in Technology, vol. 27, no. 2–3, pp. 133–143, 2006.

    Article  Google Scholar 

  39. G. Garcia and J. Bernussou, “Pole assignment for perturbed systems in a specified disk by state feedback,” IEEE Transactions on Automatic Control, vol. 40, no. 1, pp. 184–190, 1995.

    Article  MathSciNet  Google Scholar 

  40. S. K. Hong and Y. Nam, “Stable fuzzy control system design with pole-placement constraint: an LMI approach,” Computer in Industry, vol. 51, no. 1, pp. 1–11, 2003.

    Article  Google Scholar 

  41. A. Jadbabaie, M. Jamshidi, and A. Titli, “Guaranteed-cost design of continuous-time Takagi-Sugeno fuzzy controllers via linear matrix inequalities,” Proc. of IEEE International Conference on Fuzzy System, vol. 1, pp. 268–273, 1998.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Marine Engineering, National Taiwan Ocean University, Keelung, 202, Taiwan, Republic of China

    Wen-Jer Chang, Yan-Horng Lin & Chin-Ming Chang

  2. School of Marine Engineering, Dalian Maritime University, Dalian, 116026, China

    Jialu Du

Authors
  1. Wen-Jer Chang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yan-Horng Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jialu Du
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Chin-Ming Chang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wen-Jer Chang.

Additional information

Publisher's Note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Wen-Jer Chang received his B.S. degree from National Taiwan Ocean University, Taiwan, R.O.C., in 1986. The Marine Engineering is his major course and the Electronic Engineering is his minor one. He received an M.S. degree in the Institute of Computer Science and Electronic Engineering from the National Central University in 1990, and a Ph.D. degree from the Institute of Electrical Engineering of the National Central University in 1995. Since 1995, he has been with National Taiwan Ocean University, Keelung, Taiwan, R.O.C. He is currently the Dean of Academic Affairs, and a full Professor of the Department of Marine Engineering of National Taiwan Ocean University. He is now a life member of the IEEE, CIEE, CACS, CSFAT and SNAME. Since 2003, Dr. Chang was listed in the Marquis Who's Who in Science and Engineering. In 2003, he also won the outstanding young control engineers award granted by the Chinese Automation Control Society (CACS). In 2004, he won the universal award of accomplishment granted by ABI of USA. In 2005 and 2013, he was selected as an excellent teacher of the National Taiwan Ocean University. Dr. Chang has authored more than 120 published journal papers and 120 refereed conference papers. His recent research interests are marine engineering, fuzzy control, robust control, performance constrained control.

Yann-Horng Lin received his B.S. degree from the Department of Marine Engineering of the National Taiwan Ocean University, Taiwan, R.O.C., in 2016. In 2018, he received an M.S. degree in Marine Engineering from National Taiwan Ocean University, Taiwan, R.O.C, He is currently working toward a Ph.D. degree in the Department of Marine Engineering at the National Taiwan Ocean University. His research interests focus on fuzzy control, robust control, performance constrained control and intelligent control applications.

Chin-Ming Chang was born on December 27, 1960 in Taiwan, R.O.C. In 1992, he received his B.S. degree from the Department of Marine Engineering of the National Taiwan Ocean University, Taiwan, R.O.C. In 2001, he received an M.S. degree from National Taipei University of Technology, Taiwan, R.O.C. He is currently working toward a Ph.D. degree in the Department of Marine Engineering at the National Taiwan Ocean University. His research interests focus on fuzzy control, optimal control and ship control system applications.

Jialu Du received her B.E. degree in automatic control, an M.Sc. degree in power drive and automation, and a Ph.D. degree in marine engineering from Dalian Maritime University, Dalian, China, in 1988, 1991, and 2005, respectively. She was a Visiting Scholar with the Department of Engineering Cybernetics, Norwegian University of Science and Technology, Trond-heim, Norway, and with the Cymer Center for Control Systems and Dynamics, University of California at San Diego, San Diego, CA, USA. She is currently a Professor with the School of Marine Electrical Engineering, Dalian Maritime University. Her current research interests include nonlinear control theory, adaptive and robust control, intelligent control, and ship motion control.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chang, WJ., Lin, YH., Du, J. et al. Fuzzy Control with Pole Assignment and Variance Constraints for Continuous-time Perturbed Takagi-Sugeno Fuzzy Models: Application to Ship Steering Systems. Int. J. Control Autom. Syst. 17, 2677–2692 (2019). https://doi.org/10.1007/s12555-018-0917-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12555-018-0917-9

Keywords

Search

Navigation