Skip to main content
SpringerLink
Log in

Robust output tracking control for a class of uncertain nonlinear systems using extended state observer

  • Regular Papers
  • Control Theory and Applications
  • Published:
International Journal of Control, Automation and Systems Aims and scope Submit manuscript

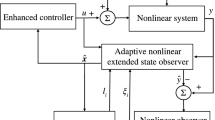
Abstract

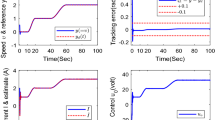
This paper investigates the global robust output tracking control problem via output feedback for a class of nonlinear uncertain systems with the integral input-to-state stable (iISS) dynamic uncertainties. By performing the coordinates transformation and employing an extended state observer (ESO), it can be seen that the robust setpoint tracking control is well solved. The proposed control strategy simplifies the control design procedure. This control scheme finds its application in the mass-spring mechanical system. It is shown that the asymptotic tracking control for any desired displacement can be achieved in the mass-spring mechanical system in the case of unknown parameters. The simulation results demonstrate that the proposed control scheme has a better tracking performance. This verifies the effectiveness of the developed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. I. Karafyllis and Z. P. Jiang, Stability and Stabilisation of Nonlinear Systems, Springer-Verlag, London, 2011.

    Book  MATH  Google Scholar 

  2. E. D. Sontag, “Smooth stabilization implies comprime factorization,” IEEE Trans. Autom. Control, vol. 34, no. 4, pp. 435–443, 1989.

    Article  MATH  Google Scholar 

  3. D. Angeli, E. D. Sontag, and Y. Wang, “A characterization of integral input to state stability,” IEEE Trans. Autom. Control, vol. 45, no. 6, pp. 1082–1087, 2000.

    Article  MathSciNet  MATH  Google Scholar 

  4. Z. P. Jiang, I. Mareels, D. J. Hill, and J. Huang, “A unifying framework for global regulation via nonlinear output feedback from ISS to iISS,” IEEE Trans. Autom. Control, vol. 49, no. 4, pp. 49–562, 2004.

    Article  MathSciNet  Google Scholar 

  5. X. Yu, Y. Q. Wu, and X. J. Xie, “Reduced-order observerbased output feedback regulation for a class of nonlinear systems with iISS inverse dynamics,” Int. J. Control, vol. 85, no. 12, pp. 1942–1951, 2012. [click]

    Article  MATH  Google Scholar 

  6. D. B. Xu, J. Huang, and Z. P. Jiang, “Global adaptive output regulation for a class of nonlinear systems with iISS inverse dynamics using output feedback,” Automatica, vol. 49, no. 7, pp. 2184–2191, 2013. [click]

    Article  MathSciNet  Google Scholar 

  7. Y. Q. Wu, J. B. Yu, and Y. Zhao, “Further results on global asymptotic regulation control for a class of nonlinear systems with iISS inverse dynamics,” IEEE Trans. Autom. Control, vol. 56, no. 4, pp. 941–946, 2011. [click]

    Article  MathSciNet  Google Scholar 

  8. X. M. Sun and W. Wang, “Integral input-to-state stability for hybrid delayed systems with unstable continuous dynamics,” Automatica, vol. 48, no. 9, pp. 2359–2364, 2012. [click]

    Article  MathSciNet  MATH  Google Scholar 

  9. S. H. Ding, J. D. Wang, and W. X. Zheng, “Secondorder sliding mode control for nonlinear uncertain systems bounded by positive functions,” IEEE Trans. Ind. Electron., vol. 62, no. 9, pp. 5899–5909, 2015.

    Article  Google Scholar 

  10. S. H. Ding, S. H. Li, and W. X. Zheng, “Nonsmooth stabilization of a class of nonlinear cascaded systems,” Automatica, vol. 48, no. 10, pp. 2597–2606, 2012. [click]

    Article  MathSciNet  MATH  Google Scholar 

  11. J. B. Yu, A. L. Shi and J. L. Yao, “Global asymptotic regulation control by output feedback for a class of nonlinear systems,” Proc. of the 34th Chinese Control Conf., pp. 895–900, 2015.

    Google Scholar 

  12. R. Freeman and P. V. Kokotović, Robust Nonlinear Control Design, Birkhäuser, Boston, 1996.

    Book  MATH  Google Scholar 

  13. Z. P. Jiang and I. Mareels, “Robust nonlinear integral control,” IEEE Trans. Autom. Control, vol. 46, no. 8, pp. 1336–1342, 2001. [click]

    Article  MathSciNet  MATH  Google Scholar 

  14. J. B. Yu and Y. Q. Wu, “Global set-point tracking control for a class of nonlinear systems and its application in continuously stirred tank reactor systems,” IET Control Theory Appl., vol. 6, no. 12, pp. 1965–1971, 2012. [click]

    Article  MathSciNet  Google Scholar 

  15. J. B. Yu, J. Z. Wang, C. X. Zhang, and Y. Q. Wu, “Output feedback regulation control for a class of uncertain nonlinear systems,” ASME J. Dyn. Syst. Meas. Control, vol. 137, no. 4, pp. 041019-1-5, 2015. [click]

    Google Scholar 

  16. K. Dupree, C. H. Liang, G. Hu, and W. E. Dixon, “Adaptive Lyapunov-based control of a robot and mass-spring system undergoing an impact collision,” IEEE Trans. on Systems, Man, and Cybernetics, Part B: Cybernetics, vol. 38, no. 4, pp. 1050–1061, 2008. [click]

    Article  Google Scholar 

  17. H. Y. Li, Y. N. Peng, and P. Shi, “Switched fuzzy output feedback control and its application to Mass-springdamping system,” IEEE Trans. Fuzzy Systems, vol. 24, no. 6, pp. 1259–1269, 2016.

    Article  Google Scholar 

  18. M. Krstić, I. Kanellakopoulos, and P. V. Kokotović, Nonlinear and Adaptive Control Design, Wiley, New York, 1995.

    MATH  Google Scholar 

  19. Z. P. Jiang and D. J. Hill, “A robust adaptive backstepping scheme for nonlinear systems with unmodeled dynamics,” IEEE Trans. Autom. Control, vol. 44, no. 9, pp. 1705–1711, 1999. [click]

    Article  MathSciNet  MATH  Google Scholar 

  20. J. Y. Yao, Z. X. Jiao, and D. W. Ma, “Extended-stateobserver-based output feedback nonlinear robust control of hydraulic systems with Backstepping,” IEEE Trans. Ind. Electron., vol. 61, no. 11, pp. 6285–6293, 2014. [click]

    Article  Google Scholar 

  21. J. Y. Yao, Z. X. Jiao, and D. W. Ma, “Adaptive robust control of DC motors with extended state observer,” IEEE Trans. Ind. Electron., vol. 61, no. 7, pp. 3630–3637, 2014. [click]

    Article  Google Scholar 

  22. J. Y. Yao, Z. X. Jiao, and D. W. Ma, “Output feedback robust control of direct current motors with nonlinear friction compensation and disturbance rejection,” ASME J. Dyn. Syst. Meas. Control, vol. 137, no. 4, pp. 041004, 2015. [click]

    Article  Google Scholar 

  23. H. L. Xing, D. H. Li, J. Li, and C. H. Zhang, “Linear extended state observer based sliding mode disturbance decoupling control for nonlinear multivariable systems with uncertainty,” Int J Contr Autom Syst, vol. 14, no. 4, pp. 1–10, 2016.

    Google Scholar 

  24. W. Y. Yu, S. T. Liu, and F. F. Zhang, “Global output feedback regulation of uncertain nonlinear systems with unknown time delay,” Int J Contr Autom Syst, vol. 13, no. 2, pp. 1–9, 2015.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Science, Shandong Jianzhu University, Jinan, 250101, P. R. China

    Yan Zhao, Jiang-Bo Yu & Jie Tian

Authors
  1. Yan Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jiang-Bo Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jie Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jiang-Bo Yu.

Additional information

Recommended by Associate Editor Do Wan Kim under the direction of Editor Jessie (Ju H.) Park. This work was supported by the Outstanding Middle-age and Young Scientist Award Foundation of Shandong Province under grant BS2015DX008, the National Natural Science Foundation of China under grant 61304008, 61471409, 61403237, and the Natural Science Foundation of Shandong Province of China under grant ZR2013FQ033. The authors would like to thank the anonymous reviewers for their valuable and constructive comments for improving the quality of this work. The authors also express their gratitude to associate Prof. Lei Yu for helpful discussions on PID control in Soochow University, China.

Yan Zhao received the B.S. and M.S. degrees in Applied Mathematics and Control Theory from Qufu Normal University, and the Ph.D. degree in Control Science and Engineering from Southeast University, in 2007, 2010 and 2014, respectively. She is currently a Lecturer in School of Science, Shandong Jianzhu University. Her research interests include stochastic nonholonomic systems control and nonlinear systems control.

Jiang-Bo Yu received the B.S. and M.S. degrees in Applied Mathematics and Control Theory from Qufu Normal University, and the Ph.D. degree in Control Science and Engineering from Southeast University, in 2006, 2009 and 2012, respectively. He is currently an Associate Professor in School of Science, Shandong Jianzhu University. His research interests include robust adaptive control and nonlinear systems control.

Jie Tian received her B.S., M.S. and Ph.D. degrees in Applied Mathematics from Qufu Normal University, in 2002, 2005 and 2008, respectively. She is currently an Associate Professor in School of Science, Shandong Jianzhu University. Her research interests include stochastic nonlinear control.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, Y., Yu, JB. & Tian, J. Robust output tracking control for a class of uncertain nonlinear systems using extended state observer. Int. J. Control Autom. Syst. 15, 1227–1235 (2017). https://doi.org/10.1007/s12555-016-0078-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12555-016-0078-7

Keywords

Search

Navigation