Abstract
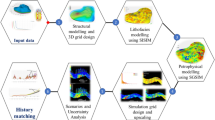
In this paper, we present a novel methodology by employing the finite element method (FEM) for creating probability fields of rock types (facies) present in a reservoir. The method is developed for a hydrocarbon reservoir, which, situated thousands of meters underground, has a high uncertainty regarding its geology. However, from the exploration phase, are collected facies observations (hard data) about the rock types present at some sparse locations of the reservoir domain. These observations are projected into a continuous probabilistic space, which is the environment of the FEM. The novelty consists of the fact that the probability field of a facies type is viewed as a deformation field of a plate. For each facies type, the FEM constructs a deformation profile which will be a probability field. The fields generated with the FEM verify the conditions of the probability theory without post-regularization techniques. We test the methodology for a two-dimensional reservoir model with three facies types. We also show the applicability of the new method by introducing the probability fields in the truncated pluri-Gaussian simulation method for simulating facies fields which are the inputs in the assisted history matching of the reservoir.












Similar content being viewed by others
References
Aanonsen SI, Nævdal G, Oliver DS, Reynolds AC, Vallès B et al (2009) The ensemble kalman filter in reservoir engineering–a review. Spe J 14(03):393–412
Abadpour A, Adejare M, Chugunova T, Deboaisne R (2017) Characterization and uncertainty reduction on facies distribution and probability cubes with ensemble Kalman filter history matching. volume Day 3 Wed, May 10, 2017 of SPE Reservoir Characterisation and Simulation Conference and Exhibition
Agbalaka C, Oliver DS (2008) Application of the EnKF and localization to automatic history matching of facies distribution and production data. Math Geosci 40(4):353–374
Astrakova A, Oliver DS (2014) Conditioning truncated pluri-Gaussian models to facies observations in ensemble-Kalman-based data assimilation. Math Geosci 47(3):345–367
Avseth P, Mukerji T, Jørstad A, Mavko G, Veggeland T (2001) Seismic reservoir mapping from 3-D, AVO in a North Sea turbidite system. Geophysics 66(4):1157–1176
Bathe K-J (1996) Finite Element Procedures. Prentice-Hall, Inc.
Belytschko T, Lu YY, Gu L (1994) Element-free galerkin methods. Int J Numer Methods Eng 37(2):229–256
Caers J, Zhang T (2004) Multiple-point geostatistics: a quantitative vehicle for integrating geologic analogs into multiple reservoir models. AAPG Spec Vol 80:383–394
Craciun EM, Barbu L (2015) Compact closed form solution of the incremental plane states in a pre-stressed elastic composite with an elliptical hole. ZAMM - J Appl Math Mech / Z Angewandte Math Mech 95 (2):193–199
Deutsch CV (2002) Geostatistical Reservoir Modeling. Oxford University Press
Esfahani NM, Asghari O (2013) Fault detection in 3d by sequential gaussian simulation of rock quality designation (rqd). Arab J Geosci 6:3737–3747
Galli A, Beucher H, Le Loc G, Doligez B et al (1994) The pros and cons of the truncated gaussian method. In: Geostatistical simulations. Springer, pp 217–233
Goovaerts P (2002) Geostatistical modelling of spatial uncertainty using p-field simulation with conditional probability fields. Int J Geogr Inf Sci 16(2):167–178
Hanea R, Ek T, Sebacher B, Sætrom J, Sollien D (2014) Geologically realistic facies updates for a north sea field. vol 2014, pp 1–5 of 76th EAGE Conference and Exhibition
Jafarpour B, Khodabakhshi M (2011) A probability conditioning method (PCM) for nonlinear flow data integration into multipoint statistical facies simulation. Math Geosci 43(2):133–164
Jalali M, Ramazi H (2017) Statistical and geostatistical approaches to study spatiotemporal uncertainties in earthquake catalog databases. Arab J Geosci 10(326)
Kumar S, Pandey P, Das S, Craciun E. -M. (2019) Numerical solution of two dimensional reaction-diffusion equation using operational matrix method based on genocchi polynomial - part i: Genocchi polynomial and operational matrix. Proc Roman Acad Ser A 20(4):393–399
Massonnat GJ, et al. (1999) Breaking of a paradigm: geology can provide 3D complex probability fields for stochastic facies modelling. In: SPE Annual Technical Conference and Exhibition, Houston, pp 329–342
Nastasescu V (1995) Analiza cu elemente finite. Editura Academiei Tehnice Militare, Bucuresti
Ng S, Dahle P, Kolbjørsen O, Hauge R et al (2008) Estimation of facies probabilities on the Snorre field using geostatistical AVA inversion. In: 2008 SEG Annual Meeting 9-14 November. Society of Exploration Geophysicists, Las Vegas
Remy N (2005) S-gems: the stanford geostatistical modeling software: a tool for new algorithms development. In: Geostatistics Banff 2004. Springer, pp 865–871
Sebacher B, Hanea R, Heemink A (2013) A probabilistic parametrization for geological uncertainty estimation using the ensemble Kalman filter (EnKF). Comput Geosci 17(5):813–832
Sebacher B, Stordal A, Hanea R (2015) Bridging Multi Point Statistics and Truncated Gaussian Fields for Improved Estimation ofChannelized Reservoirs with Ensemble Methods. Comput Geosc 19(2):341–369. https://doi.org/10.1007/s10596-014-9466-3
Sebacher B, Stordal A, Hanea R (2016) Complex geology estimation using the iterative adaptive Gaussian mixture filter. Comput Geosci 20(1):133–148. https://doi.org/10.1007/s10596-015-9553-0
Sebacher B, Hanea R, Stordal A (2017) An adaptive pluri-gaussian simulation model for geological uncertainty quantification. J Pet Sci Eng 158:494–508
Zienkiewicz O, Taylor R (1993) The finite element method, 4th edn. McGraw-Hill, London
Acknowledgements
The authors would like to thanks Prof. Dr. Vasile Nastasescu for his extraordinary support and guidance during the study process.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no competing interests.
Additional information
Responsible Editor: Zeynal Abiddin Erguler
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Marzavan, S., Sebacher, B. A new methodology based on finite element method (FEM) for generation of the probability field of rock types from subsurface. Arab J Geosci 14, 843 (2021). https://doi.org/10.1007/s12517-021-07114-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12517-021-07114-2