1 Introduction

A large number of papers in the field of queueing theory have appeared to analyze the waiting line system with an unreliable server. Among some earlier works in this area, Gaver (1962) studied the waiting line with interrupted service, including priorities. Avi-ltzhak and Naor (1963) and Thiruvengadam (1963) investigated some fundamental queueing problems with service facilities subject to breakdowns. Mitrany and Avi-Itzhak (1968) extended the analysis to the multi-server queue with service interruptions. Later, this model was revisited by Neuts and Lucantoni (1979) under the assumption that failed servers are repaired by one of the c repairmen. Over the past thirty years, authors like Sengupta (1990), Takine and Sengupta (1997), Tang (1997), Li et al. (1997), Madan (2003), Ke (2003, 2006), Wang (2004), Gray et al. (2004), Wang et al. (2010), Choudhury and Deka (2012), Jain et al. (2013), Kumar et al. (2020), Gorbunova and Lebedev (2020), and Kumar et al. (2021) have studied some single arrival queueing systems with an unreliable server. A common assumption in the above literature is that as soon as the server fails, it instantaneously undergoes repairs. However, in real-life situations, due to some unavoidable reasons, the repair of the failed server may be delayed. This phenomenon stimulates Choudhury and Tadj (2009), Choudhury and Kalita (2018) investigated the steady-state behavior of the unreliable M/G/1 queue with delay repair. On the other hand, from the mathematical and practical points of view, the case of batch arrival is more general, and also more challenging to handle. Many authors have contributed to the theory of batch arrival queues subject to unpredictable server breakdowns. Some notable works in this direction can be found in Ke and Lin (2006), Ke and Huang (2010, 2012), Choudhury and Tadj (2011), Singh et al. (2018), Choudhury and Deka (2018), Saggou et al. (2019), Jain and Kaur (2020). To get a more comprehensive summary of the recent research work on the topic of the unreliable queue, interested readers may refer to the review paper done by Jain et al. (2019a, 2019b).

It is worth noting that in the queueing systems mentioned above, the status of a server is usually modeled with two extreme states, working and failed. A working server is capable of serving customers at any instant of time. On the contrary, when the server fails, it is totally incapable of servicing and requires renewal or repair. However, such an assumption is not always true in reality. For example, a service facility or a manufacturing system built with fault tolerance capabilities will manage to keep operating (perhaps at a degraded level) in the presence of partial failure. Here, fault tolerance refers to the ability of a system to continue working without interruption when a partial failure occurs, wherein partial failures are often caused by the wear and tear of equipment components or the wrong action by an operator. The objective of creating a fault-tolerant system is to prevent disruptions arising in the service or manufacturing process, ensuring the high availability and business continuity of a stochastic service system. To theoretically analyze such phenomenon, Kalidass and Kasturi (2012) developed a new concept of working breakdowns in queueing theory. In a working breakdown queue, the server works at a lower service rate rather than completely stopping service during the breakdown period. Many researchers motivated by their work have extended this type of queue in different frameworks. Kim and Lee (2014) further studied an M/G/1 queue with disasters and working breakdowns, in which the system is equipped with a substitute server for providing the working breakdown services to arriving customers. Liu and Song (2014) extended the idea in Kalidass and Kasturi (2012) to the Markovian batch arrival queue. Applying the matrix-geometric method (Neuts 1981), Liou (2015) also investigated M/M/1 unreliable queue subject to working breakdowns and impatient customers. Other recent works on queues with working breakdowns can be found in Li et al. (2013), Yen et al. (2016), Chen (2018), Ye and Liu (2018), Jain et al. (2019a, 2019b), Jiang and Xin (2019), and Gao et al. (2019). It is, however, slightly regrettable that very few authors have studied the working breakdown queue under general renewal arrivals. To date, only a small amount of literature has covered this topic. Using the embedded Markov chain and matrix analytic approach, Jiang and Liu (2017) considered the GI/M/1 queue with disasters and working breakdowns in a multi-phase service environment. Utilizing the supplementary variable technique (Cox 1955), Yang and Cho (2019) presented a recursive algorithm for computing the stationary queue-length distribution in N-policy GI/M/1/K queue with modified working breakdowns. Here, Yang and Cho did not assume that service and maintenance can be performed simultaneously. In their model assumptions, the repairman repairs the partially failed service facility when there are no customers queueing up for service. We think this assumption may be valid in some cases. For example, as the COVID-19 pandemic has spread across the globe, the severe shortage of medical masks caused by the health crisis quickly becomes a significant issue of the pandemic. To address the growing demand for masks during the outbreak of coronavirus disease, Honeywell, a leading manufacturer of personal protective equipment, quickly ramps up production by reducing regular equipment maintenance frequency. Such maintenance schedule adjustment can be regarded as a fault-tolerance mechanism in the production process that simultaneously provides a timely response to customer needs. This example also gives us a realistic background to study the queueing system with fault-tolerant operations.

It is an indisputable fact that queueing models with customers arriving in batches rather than singly have many applications in practice, for example, in flexible manufacturing systems. However, based on the above literature review, we may see that current research has not paid much attention to the renewal batch arrival queue with working breakdowns or with fault tolerance characteristics. Such a situation prompted us to study a bulk queue with renewal input and fault-tolerant operating modes. Also, to simplify the analytical study of the model, an alternative yet simple method with resorting to the supplementary variable technique and the shift operator technique in solving difference equations is employed to analyze our model. We note that in the past one year, Barbhuiya and Gupta (2019a, 2019b, 2020) used this unique method to reconsider the algorithm for computing the queue-length distributions in some renewal input bulk arrival queues. From their pioneering work, it was revealed that the algorithm based on the combination of these two techniques is easy to understand, and can be conveniently implemented by applying a suitable software package such as Maple, Mathematica or Matlab. More importantly, this method requires neither derivation of the transition probability matrix of the Markov chain embedded at arrival instants nor the inversion of any probability generating function. We quickly realized that a more generic version of this method could be developed and applied to analyze our queueing model presented in this work.

The remaining part of our paper is organized as follows. We first describe the system and provide basic assumptions in Sect. 2. The differential-difference equations governing the queueing model are framed by the supplementary variable technique in Sect. 3. In Sect. 4, with the help of the theory of difference equation, we provide the procedure to analyze the steady-state queue-length distributions at different epochs of our model. Moreover, using the queue-length distribution at the pre-arrival epoch, we also evaluate the sojourn time of an arbitrary customer in Sect. 5. To validate the correctness of our theoretical results, we present some numerical examples in Sect. 6. Section 7 concludes the paper and directs possible further studies.

2 Model formulation and preliminaries

The mathematical model for this work describes as follows:

  • Consider GI\(^X\)/M/1 queue with a fault-tolerant server wherein batches of customers arrive at epochs \(0=\tau _0\), \(\tau _1\), \(\tau _2\), \(\ldots\), \(\tau _n\), \(\ldots\). The number of arrivals at each epoch is given by a random variable X having general distribution \(g_i=\Pr \left\{ X=i\right\}\), \(i=1,2,\ldots\), and probability generating function (p.g.f.) \(G(z)=\sum \nolimits _{i=1}^\infty g_iz^i\), \(|z|\le 1\). In most real-life situations, batch sizes are not infinite but finite. Thus, from a realistic and computational point of view, we suppose that the maximum batch size is b throughout this paper. As a result of this assumption, the p.g.f. and mean of the random variable X are given by \(G(z)=\sum \nolimits _{i=1}^bg_iz^i\) and \(\bar{g}=\sum \nolimits _{i=1}^big_i\), respectively.

  • The inter-arrival times \(\tau _{n+1}-\tau _n>0\), \(n=0,1,2,\ldots\), are independent and identically distributed (i.i.d.) random variables with common distribution function A(t) and probability density function (p.d.f.) a(t). Let the Laplace-Stieltjes transform of this distribution be denoted by \(a^*(s)=\int _0^\infty e^{-st}\mathrm{d}A(t)\) and let the mean inter-arrival time be denoted by \(1/\lambda\), where \(0<1/\lambda =\left. -\frac{\mathrm{d}}{\mathrm{d}s}a^*(s)\right| _{s=0}<\infty\).

  • The customers are served individually by a single server on a first-come, first-served basis. If \(S_n\) is the service time of the nth customer to be served in normal state, then it is assumed that \(\left\{ S_n, n=1,2,3,\ldots \right\}\) is a sequence of positive i.i.d. random variables with the common exponential p.d.f. \(\mu _0e^{-\mu _0t}\), \(t>0\).

  • A partial failure of the server could occur during the normal busy period, and the time until the random partial breakdown of the server, denoted by L, is assumed to be exponentially distributed with rate \(\eta\).

  • When a partial failure occurs, the server continues working in degraded mode at a reduced service rate rather than entirely halting service. Let \({\tilde{S}}_n\) represent the service time of the nth customer to be served in defective state, and we also assume that the sequence \(\left\{ {\tilde{S}}_n, n=1,2,3,\ldots \right\}\) are i.i.d. positive random variables following exponential distribution with parameter \(\mu _1\) \((\mu _1<\mu _0)\).

  • Given customers’ sensitivity and emotional reaction to delay, and also to ensure continuity and efficient service process, the defective server is repaired after the system becomes empty. In other words, when there are customers present in the queue, the server cannot be repaired, even if the server is undergoing repairs. The repair time of the defective server is exponentially distributed with a mean rate \(\beta\).

  • It is further supposed that various stochastic processes involved in the queueing system are mutually independent. Additionally, for the stationary analysis of the model, we demands that \(\rho ={\bar{g}}\lambda /\mu _1<1\) (see the proof of Theorems 1 and 2).

3 Governing equations of the system

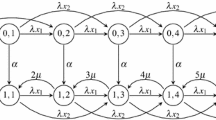
Let N(t) and \(\xi (t)\) indicate the number of customers in the system (including the one being served) and the state of the server at time t, respectively. Here, \(\xi (t)\) is a binary random variable. \(\xi (t)=0\) represents that the server is in a normal state, while \(\xi (t)=1\) represents that the server is defective. Moreover, the supplementary variable R(t) corresponding to the remaining inter-batch arrival time at time t is used, which provides Chapman–Kolmogorov equations governing our current model. Thus, the state of the system at time t could be described by a multivariate stochastic process \(\Theta (t)=\left\{ N(t),\xi (t),R(t), t\ge 0\right\}\). In this process, the non-Markovian queueing process becomes Markovian by having the necessary information so that the future of the process depends only on its current state. To ease us into the analysis of such a queue, we define the joint probabilities as follows

$$\begin{aligned}&\pi _{n,m}(x,t)\mathrm{d}x=\Pr \left\{ N(t)=n, \xi (t)=m, x<R(t)\le x+\mathrm{d}x\right\} ,\\&x\ge 0,\quad n=0,1,2,\ldots ,\quad m=0,1. \end{aligned}$$

In steady-state, let us further define

$$\begin{aligned}&Q_{n,m}(x)=\lim \limits _{t\rightarrow \infty }\pi _{n,m}(x,t), \quad n=0,1,2,\ldots , \quad m=0,1;\\&Q_{n,m}=\int _0^\infty Q_{n,m}(x)\mathrm{d}x, \quad n=0,1,2,\ldots , \quad m=0,1. \end{aligned}$$

To obtain the steady-state probabilities of the queue size \(Q_{n,0}\) and \(Q_{n,1}\), we first construct the differential-difference equations for describing the evolution of the model by observing the state of the queue at two consecutive time epochs t and \(t+\Delta t\). Using the probabilistic argument, we can derive the following set of equations:

$$\begin{aligned} -\frac{\mathrm{d}}{\mathrm{d}x}Q_{0,0}(x)&=\mu _0Q_{1,0}(x)+\beta Q_{0,1}(x), \end{aligned}$$
(1)
$$\begin{aligned} \quad -\frac{\mathrm{d}}{\mathrm{d}x}Q_{n,0}(x)&=-\left( \mu _0+\eta \right) Q_{n,0}(x)+\mu _0Q_{n+1,0}(x)\nonumber \\&\quad +a(x)\sum \limits _{i=1}^n g_{i}Q_{n-i,0}(0), \quad 1\le n \le b - 1,\end{aligned}$$
(2)
$$\begin{aligned} \quad -\frac{\mathrm{d}}{\mathrm{d}x}Q_{n,0}(x)&=- \left( \mu _0+\eta \right) Q_{n,0}(x)+\mu _0Q_{n+1,0}(x)\nonumber \\&\quad +a(x) \sum \limits _{i=1}^b g_{i}Q_{n-i,0}(0), \quad n\ge b,\end{aligned}$$
(3)
$$\begin{aligned} \quad -\frac{\mathrm{d}}{\mathrm{d}x}Q_{0,1}(x)&=-\beta Q_{0,1}(x)+\mu _1Q_{1,1}(x),\end{aligned}$$
(4)
$$\begin{aligned} \quad -\frac{\mathrm{d}}{\mathrm{d}x}Q_{n,1}(x)&=- \mu _1Q_{n,1}(x)+ \mu _1Q_{n+1,1}(x) +\eta Q_{n,0}(x)\nonumber \\&\quad +a(x) \sum \limits _{i=1}^n g_{i}Q_{n-i,1}(0), \quad 1 \le n \le b -1,\end{aligned}$$
(5)
$$\begin{aligned} \quad -\frac{\mathrm{d}}{\mathrm{d}x}Q_{n,1}(x)&=-\mu _1Q_{n,1}(x)+\mu _1Q_{n+1,1}(x)+\eta Q_{n,0}(x)\nonumber \\&\quad +a(x)\sum \limits _{i=1}^bg_iQ_{n-i,1}(0), \quad n\ge b. \end{aligned}$$
(6)

Since the Laplace transform are extremely useful in the solution of complicated differential-difference equations presented above, we define the Laplace transform of \(Q_{n,m}(x)\) as

$$\begin{aligned} Q_{n,m}^*(s)=\int _0^\infty e^{-sx}Q_{n,m}(x)\mathrm{d}x, \quad n=0,1,2,\ldots , \quad m=0,1. \end{aligned}$$

Meanwhile, we also notice that \(Q_{n,m}^*(0) = Q_{n,m}\). Then, taking the Laplace transform on both sides of Eqs. (1)–(6) and using the relation \(-\int _0^\infty e^{-sx}\frac{\mathrm{d}}{\mathrm{d}x}Q_{n,m}(x)\mathrm{d}x=Q_{n,m}(0)-sQ_{n,m}^*(s)\), we thus obtain the transformed equations as below

$$\begin{aligned} -sQ_{0,0}^*(s)&= -Q_{0,0}(0)+\mu _0Q_{1,0}^*(s)+\beta Q_{0,1}^*(s),\end{aligned}$$
(7)
$$\begin{aligned} \left( \mu _0+\eta -s\right) Q_{n,0}^*(s)&= -Q_{n,0}(0)+\mu _0Q_{n+1,0}^*(s)\nonumber \\&\quad +a^*(s)\sum \limits _{i=1}^n g_{i}Q_{n-i,0}(0), \quad 1\le n\le b -1,\end{aligned}$$
(8)
$$\begin{aligned} \left( \mu _0+\eta -s\right) Q_{n,0}^*(s)&= -Q_{n,0}(0)+\mu _0Q_{n+1,0}^*(s)\nonumber \\&\quad +a^*(s)\sum \limits _{i=1}^b g_{i}Q_{n-i,0}(0), \quad n\ge b,\end{aligned}$$
(9)
$$\begin{aligned} \left( \beta -s\right) Q_{0,1}^*(s)&= -Q_{0,1}(0)+\mu _1Q_{1,1}^*(s),\end{aligned}$$
(10)
$$\begin{aligned} \left( \mu _1 - s\right) Q_{n,1}^*(s)&= -Q_{n,1}(0)+\mu _1Q_{n+1,1}^*(s)+\eta Q_{n,0}^*(s)\nonumber \\&\quad +a^*(s) \sum \limits _{i=1}^n g_{i}Q_{n-i,1}(0), \quad 1\le n \le b -1,\end{aligned}$$
(11)
$$\begin{aligned} \left( \mu _1 -s\right) Q_{n,1}^*(s)&= -Q_{n,1}(0)+\mu _1Q_{n+1,1}^*(s)+\eta Q_{n,0}^*(s)\nonumber \\&\quad +a^*(s) \sum \limits _{i=1}^bg_iQ_{n-i,1}(0), \quad n\ge b. \end{aligned}$$
(12)

Adding Eqs. (7)–(12), it yields

$$\begin{aligned} \sum \limits _{n=0}^\infty Q_{n,0}^*(s)+\sum \limits _{n=0}^\infty Q_{n,1}^*(s)=\frac{1-a^*(s)}{s}\left( \sum \limits _{n=0}^\infty Q_{n,0}(0)+\sum \limits _{n=0}^\infty Q_{n,1}(0)\right) . \end{aligned}$$
(13)

Taking the limit as \(s\rightarrow 0\), and using L’H\(\hat{\mathrm{o}}\)spital’s rule one time in the above Eq. (13), we have

$$\begin{aligned} \sum \limits _{n=0}^\infty Q_{n,0}^*(0)+\sum \limits _{n=0}^\infty Q_{n,1}^*(0)=\frac{1}{\lambda }\left( \sum \limits _{n=0}^\infty Q_{n,0}(0)+\sum \limits _{n=0}^\infty Q_{n,1}(0)\right) . \end{aligned}$$
(14)

Here, the normalization condition implies that

$$\begin{aligned} \sum \limits _{n=0}^\infty Q_{n,0}^*(0)+\sum \limits _{n=0}^\infty Q_{n,1}^*(0)=1. \end{aligned}$$
(15)

Substituting Eq. (15) into Eq. (14), we get

$$\begin{aligned} \sum \limits _{n=0}^\infty Q_{n,0}(0)+\sum \limits _{n=0}^\infty Q_{n,1}(0)=\lambda . \end{aligned}$$
(16)

Employing Eq. (16), we may show that if \(Q_{n,m}^-\) represents the steady-state probability of having n \((n\ge 0)\) customers in the system and the server being in state m \((m=0,1)\) immediately before batch arrival, then \(Q_{n,m}^-=\frac{1}{\lambda }Q_{n,m}(0)\). To show this, it should be noted that \(Q_{n,m}^-\) is proportional to \(Q_{n,m}(0)\) and \(\sum \nolimits _{n=0}^\infty Q_{n,0}(0)+\sum \nolimits _{n=0}^\infty Q_{n,1}(0)\), which gives

$$\begin{aligned} Q_{n,m}^-=\frac{Q_{n,m}(0)}{\sum \limits _{n=0}^\infty Q_{n,0}(0)+\sum \limits _{n=0}^\infty Q_{n,1}(0)}=\frac{1}{\lambda }Q_{n,m}(0). \end{aligned}$$
(17)

Now, we have already seen that once \(Q_{n,m}(0)\) and \(Q_{n,m}^*(s)\) are obtained, we can further use them to get the queue-length distributions at the instant of a batch arrival (\(Q_{n,m}^-\)) and arbitrary epoch (\(Q_{n,m}\)). We will address how to deal with this problem in the next section.

4 Queue-length distributions at pre-arrival and arbitrary epochs

For analysis purposes, the discrete variable n will be considered to be the independent variable, while the function values \(Q_{n,m}(0)\) and \(Q_{n,m}^*(s)\) \((m=0,1)\) will be the dependent variables. For the sequences \(\left\{ Q_{n,m}(0),n\ge 0\right\}\) and \(\left\{ Q_{n,m}^*(s),n\ge 0\right\}\), we define a right shift operator \({\mathbb {T}}\) on the above two sequences and set \({\mathbb {T}}^jQ_{n,m}(0)=Q_{n+j,m}(0)\) and \({\mathbb {T}}^jQ_{n,m}^*(s)=Q_{n+j,m}^*(s)\), \(j\ge 1\). Thus, Eq. (9) can now be written in terms of operator \({\mathbb {T}}\) as follows

$$\begin{aligned} (s-\eta -\mu _0+\mu _0{\mathbb {T}})Q_{n,0}^*(s)=\left( {\mathbb {T}}^b-a^*(s)\sum \limits _{i=1}^bg_i{\mathbb {T}}^{b-i}\right) Q_{n-b,0}(0), \quad n\ge b. \end{aligned}$$
(18)

By setting \(n\ge 0\) instead of \(n\ge b\) and substituting \(s=\eta +\mu _0-\mu _0{\mathbb {T}}\), Eq. (18) reduces to the below homogeneous difference equation with constant coefficients

$$\begin{aligned} \left( {\mathbb {T}}^b-a^*(\eta +\mu _0-\mu _0{\mathbb {T}})\sum \limits _{i=1}^bg_i{\mathbb {T}}^{b-i}\right) Q_{n,0}(0)=0, \quad n\ge 0. \end{aligned}$$
(19)

According to the fundamental theory of difference equation, the corresponding auxiliary equation

$$\begin{aligned} z^b-a^*(\eta +\mu _0-\mu _0z)\sum \limits _{i=1}^bg_iz^{b-i}=0 \end{aligned}$$
(20)

is said to be the characteristic equation of Eq. (19). Next, we will apply Rouch\(\acute{\mathrm{e}}\)’s theorem to find the number of roots of Eq. (20).

Theorem 1

When \(\frac{{\bar{g}}\lambda }{\mu _0}<1\), the characteristic equation \(z^b-a^*(\eta +\mu _0-\mu _0z)\sum \nolimits _{i=1}^bg_iz^{b-i}=0\) has exactly b roots inside the unit disk.

Proof

Consider two complex-valued functions \(f(z)=z^b\) and \(g(z)=-a^*(\eta +\mu _0-\mu _0z)\sum \nolimits _{i=1}^bg_iz^{b-i}\). Let \(H(z)=a^*(\eta +\mu _0-\mu _0z)\). Clearly, for a sufficiently small \(\delta >0\), H(z) is holomorphic inside and on the closed contour \(|z|=1+\delta\). Thus, according to the Taylor’s theorem for analytic complex function there exists a power series \(\sum \nolimits _{k=0}^\infty h_k(z-1)^k\) which converges to H(z). The coefficients \(h_k\) \((k=0,1,2,\ldots )\) are given by \(h_k=\frac{1}{2\pi \mathbf{i}}\oint _{\mathbb {C}}\frac{H(z)}{(z-1)^{k+1}}\mathrm{d}z=\frac{{H^{(k)}}(1)}{k!}\), where \({\mathbf{i}}=\sqrt{-1}\) and \({\mathbb {C}}\) is any closed contour around 1 and lying completely inside \(|z|\le 1+\delta\). Then, employing the Taylor expansion for H(z), we may estimate |f(z)| and |g(z)| on the simple closed curve \(|z|=1-\epsilon\), where \(\epsilon >0\) and is also a sufficiently small quantity. Thus, on \(|z|=1-\epsilon\)

$$\begin{aligned} |f(z)|&=\left( 1-\epsilon \right) ^b=1-b\epsilon +o(\epsilon ),\\ |g(z)|&=|H(z)|\left| \sum \limits _{i= 1}^bg_iz^{b-i}\right| \le H(|z|)\sum \limits _{i=1}^bg_i|z|^{b-i}=H(1-\epsilon )\sum \limits _{i=1}^bg_i(1-\epsilon )^{b-i}\\&\quad =\left[ H(1)+\frac{H'(1)}{1!}(1-\epsilon -1)+\sum \limits _{k=2}^\infty \frac{H^{(k)}(1)}{k!}(1-\epsilon -1)^k\right] \sum \limits _{i=1}^bg_i\left[ 1-(b-i)\epsilon +o(\epsilon )\right] \\&\quad =\left[ \int _0^\infty (1-\epsilon \mu _0t)e^{-\eta t}\mathrm{d}A(t)+o(\epsilon )\right] \sum \limits _{i=1}^bg_i\left[ 1-(b-i)\epsilon +o(\epsilon )\right] \\&\quad \le \left[ \int _0^\infty (1-\epsilon \mu _0t)\mathrm{d}A(t)+o(\epsilon )\right] \sum \limits _{i=1}^bg_i\left[ 1-(b-i)\epsilon +o(\epsilon )\right] \\&\quad =\left[ 1-\frac{\mu _0}{\lambda }\epsilon +o(\epsilon )\right] \left[ 1+{\bar{g}}\epsilon -b\epsilon +o(\epsilon )\right] \\&\quad =1-b\epsilon +\left( \bar{g}-\frac{\mu _0}{\lambda }\right) \epsilon +o(\epsilon )\le |f(z)| \end{aligned}$$

Consequently, as all the conditions of Rouch\(\acute{\mathrm{e}}\)’s theorem (see Klimenok 2001) are satisfied, \(f(z)+g(z)\) has exactly b zeros inside the unit circle, since f(z) has b. \(\square\)

It has been shown by many authors that in queueing theory, roots of the characteristic equation are well structured, and they are generally distinct, see, e.g., Tijms (2003) and Chaudhry et al. (1990). Therefore, if we assume that the roots of Eq. (20) are distinct, denoted by \(r_j, j=1,2,\ldots ,b\), the general solution of Eq. (19) can be expressed in the form

$$\begin{aligned} Q_{n,0}(0)=\sum \limits _{j=1}^b\phi _jr_j^n, \quad n\ge 0, \end{aligned}$$
(21)

where \(\phi _j\) \((j=1,\ldots ,b)\) are real or complex constants to be determined. Substituting Eq. (21) into Eq. (18) yields

$$\begin{aligned} (s-\eta -\mu _0+\mu _0{\mathbb {T}})Q_{n,0}^*(s)=\left( {\mathbb {T}}^b-a^*(s)\sum \limits _{i=1}^bg_i{\mathbb {T}}^{b-i}\right) \sum \limits _{j=1}^b\phi _jr_j^{n-b}, \quad n\ge b. \end{aligned}$$
(22)

It is now necessary to turn to determine the unknown function \(Q_{n,0}^*(s)\) from the above equation. Treating s as a fixed constant, Eq. (22) can be regarded as a first order nonhomogeneous difference equation with constant coefficients and its general solution consists of two parts: solution to the corresponding homogeneous equation plus a particular solution to the nonhomogeneous equation. For Eq. (22), the general solution of the homogeneous part is written as \(Q_{n,0}^{*(\hom )}(s)=D_1\left( 1+\frac{\eta -s}{\mu _0}\right) ^n\), where \(D_1\) is an arbitrary constant. On the other hand, we note that an appropriate trial solution for \((s -\eta -\mu _0+\mu _0{\mathbb {T}})Q_{n,0}^*(s)=\left( r_j^{-b}{\mathbb {T}}^b -a^*(s)\sum \nolimits _{i=1}^bg_ir_j^{-b}{\mathbb {T}}^{b-i}\right) \phi _jr_j^n\) is \(Q_{n,0}^*(s) = d_jr_j^n\), \(j = 1,2,\ldots ,b\). Thus, a particular solution of the nonhomogeneous Eq. (22) can be given as follows

$$\begin{aligned} Q_{n,0}^{*(\mathrm{part})}(s)=\sum \limits _{j=1}^b\frac{\phi _j\left[ r_j^b-a^*(s)\sum \limits _{i=1}^bg_ir_j^{b-i}\right] }{s-\eta -\mu _0(1-r_j)}r_j^{n-b}, \quad n\ge b. \end{aligned}$$
(23)

Adding this particular solution to the general solution of the associated homogeneous equation, the solution of Eq. (22) is presented as

$$\begin{aligned} Q_{n,0}^{*}(s)=D_1\left( 1+\frac{\eta -s}{\mu _0}\right) ^n+\sum \limits _{j=1}^b\frac{\phi _j\left[ r_j^b-a^*(s)\sum \limits _{i=1}^bg_ir_j^{b-i}\right] }{s-\eta -\mu _0(1-r_j)}r_j^{n-b}, \quad n\ge b. \end{aligned}$$
(24)

As s tends to zero, since \(\sum \nolimits _{n=b}^\infty Q_{n,0}^{*}(0)=\sum \nolimits _{n=b}^\infty Q_{n,0}<1\), we must have \(D_1=0\), otherwise the sum \(\sum \nolimits _{n=b}^\infty Q_{n,0}\) will diverge. Hence, Eq. (24) reduces to

$$\begin{aligned} Q_{n,0}^{*}(s)=\sum \limits _{j=1}^b\frac{\phi _j\left[ r_j^b-a^*(s)\sum \limits _{i=1}^bg_ir_j^{b-i}\right] }{s-\eta -\mu _0(1-r_j)}r_j^{n-b}= \sum \limits _{j=1}^b\frac{\phi _j\left[ r_j^n-a^*(s)\sum \limits _{i=1}^bg_ir_j^{n-i}\right] }{s-\eta -\mu _0(1-r_j)}, \quad n\ge b. \end{aligned}$$
(25)

We now find the conditions under which \(Q_{n,0}^*(s)\) has the same expression as in Eq. (25) for \(1\le n\le b-1\). To this end, substituting Eq. (21) into Eqs. (8) and (9), and comparing the last term of the right hand side of the above two equations, we may observe that the unknown constants \(\phi _j\) satisfy the relationship

$$\begin{aligned} a^*(s)\sum \limits _{i=1}^n g_{i} \sum \limits _{j=1}^b\phi _jr_j^{n-i}= & {} a^*(s) \sum \limits _{i=1}^b g_{i}\sum \limits _{j=1}^b\phi _jr_j^{n-i} \nonumber \\&\Rightarrow \sum \limits _{j=1}^b\phi _j\sum \limits _{i=n+1}^b g_{i}r_{j}^{n-i}=0, \quad 1 \le n \le b -1. \end{aligned}$$
(26)

Respectively setting \(n=b-1,b-2,\ldots ,1\) in Eq. (26) and noting that \(g_b\ne 0\), we can construct a system of \(b-1\) linear equations in b variables which can be employed to determine the unknown constants \(\phi _j\) \((j=1,2,\ldots ,b)\) in later analysis

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{\phi _1}{r_1}+\frac{\phi _2}{r_2}+\cdots +\frac{\phi _{b-1}}{r_{b-1}}+\frac{\phi _b}{r_b}=0,\\ \displaystyle \frac{\phi _1}{r_1^2}+\frac{\phi _2}{r_2^2}+\cdots +\frac{\phi _{b-1}}{r_{b-1}^2}+\frac{\phi _b}{r_b^2}=0,\\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ \displaystyle \frac{\phi _1}{r_1^{b-2}}+\frac{\phi _2}{r_2^{b-2}}+\cdots +\frac{\phi _{b-1}}{r_{b-1}^{b-2}}+\frac{\phi _b}{r_b^{b-2}}=0,\\ \displaystyle \frac{\phi _1}{r_1^{b-1}}+\frac{\phi _2}{r_2^{b-1}}+\cdots +\frac{\phi _{b-1}}{r_{b-1}^{b-1}}+\frac{\phi _b}{r_b^{b-1}}=0. \end{array}\right. \end{aligned}$$
(27)

If the above results hold true, for any \(n\ge 1\)

$$\begin{aligned} Q_{n,0}^{*}(s)=\sum \limits _{j=1}^b\frac{\phi _j\left[ r_j^n-a^*(s)\sum \limits _{i=1}^bg_ir_j^{n-i}\right] }{s-\eta -\mu _0(1-r_j)}. \end{aligned}$$
(28)

Next, let us once again apply the right shift operator \({\mathbb {T}}\) to Eq. (12). Then, we have

$$\begin{aligned} (s-\mu _1+\mu _1{\mathbb {T}})Q_{n,1}^*(s)=\left( {\mathbb {T}}^b-a^*(s)\sum \limits _{i=1}^bg_i{\mathbb {T}}^{b-i}\right) Q_{n-b,1}(0)-\eta Q_{n,0}^*(s), \quad n\ge b. \end{aligned}$$
(29)

By setting \(s=\mu _1-\mu _1{\mathbb {T}}\) in Eq. (29) and substituting Eq. (28) into Eq. (29) yields

$$\begin{aligned}&\left[ {\mathbb {T}}^b-a^*\left( \mu _1-\mu _1{\mathbb {T}}\right) \sum \limits _{i=1}^bg_i{\mathbb {T}}^{b-i}\right] Q_{n,1}(0)=\eta Q_{n+b,0}^*(\mu _1-\mu _1{\mathbb {T}})\nonumber \\&\quad =\eta \sum \limits _{j=1}^b\frac{\phi _j\left[ r_j^b-a^*(\mu _1-\mu _1{\mathbb {T}})\sum \limits _{i=1}^bg_ir_j^{b-i}\right] }{\mu _1-\mu _1{\mathbb {T}}-\eta -\mu _0(1-r_j)}r_j^n, \quad n\ge 0. \end{aligned}$$
(30)

Adopting Rouch\(\acute{\mathrm{e}}\)’s theorem similar to that used for the previous Theorem 1, the following Theorem 2 shows that under certain conditions, the characteristic equation of the above difference equation also has exactly b roots inside the unit circle \(|z|=1\). We shall use the letters \(\omega _1\), \(\omega _2\), \(\ldots\), \(\omega _b\) to denote these b roots.

Theorem 2

When \(\frac{{\bar{g}}\lambda }{\mu _1}<1\), the characteristic equation \(z^b-a^*(\mu _1-\mu _1z)\sum \nolimits _{i=1}^bg_iz^{b-i}=0\) has exactly b roots inside the unit disk.

Furthermore, combining the results of Theorems 1 and Theorem 2, the obvious stability condition of the current queueing system is that \(\frac{{\bar{g}}\lambda }{\mu _1}<1\). By analogy with the corresponding procedure to compute \(Q_{n,0}^*(s)\), the general solution of the nonhomogeneous Eq. (30) is given by

$$\begin{aligned} Q_{n,1}(0)=\sum \limits _{j=1}^bk_j\omega _j^n+\eta \sum \limits _{j=1}^b\frac{\phi _j}{(\mu _1-\mu _0)(1-r_j)-\eta }r_j^n, \quad n\ge 0. \end{aligned}$$
(31)

Here, the first term in the right-hand side of Eq. (31) is a solution to the associated homogeneous equation of Eq. (30), and \(k_1\), \(k_2\), \(\ldots\), \(k_b\) are the arbitrary constants that can be obtained from later analysis. On the other hand, the second term is a particular solution of Eq. (30). Substituting Eqs. (28) and (31) into the right-hand side of Eq. (29), we have

$$\begin{aligned} (s -\mu _1+\mu _1{\mathbb {T}})Q_{n,1}^*(s)= & {}\, \left( {\mathbb {T}}^b -a^*(s)\sum \limits _{i=1}^bg_i{\mathbb {T}}^{b-i} \right) \left( \sum \limits _{j=1}^bk_j\omega _j^{n-b}\right. \nonumber \\&\left. +\eta \sum \limits _{j=1}^b\frac{\phi _j}{(\mu _1 -\mu _0)(1 -r_j) -\eta }r_j^{n-b}\right) \nonumber \\&-\eta \sum \limits _{j=1}^b\frac{\phi _j\left[ r_j^n-a^*(s)\sum \limits _{i=1}^bg_ir_j^{n-i}\right] }{s-\eta -\mu _0(1-r_j)},\nonumber \\= & {} \sum \limits _{j=1}^bk_j\omega _j^n -a^*(s)\sum \limits _{j=1}^bk_j\sum \limits _{i=1}^bg_i\omega _j^{n-i}\nonumber \\&+\eta \sum \limits _{j=1}^b \frac{\phi _j\left( r_j^n -a^*(s)\sum \limits _{i=1}^bg_ir_j^{n-i}\right) }{(\mu _1-\mu _0)(1-r_j)-\eta }\nonumber \\&-\eta \sum \limits _{j=1}^b\frac{\phi _j\left[ r_j^n-a^*(s)\sum \limits _{i=1}^bg_ir_j^{n-i}\right] }{s-\eta -\mu _0(1-r_j)}, \quad n\ge b, \end{aligned}$$
(32)

which is also a nonhomogeneous difference equation with constant coefficients. Similar to the discussions surrounding Eq. (22), we of course first find the general solution of the associated homogeneous equation of Eq. (32). It has the form \(Q_{n,1}^{*(\hom )}(s)=D_2\left( 1-\frac{s}{\mu _1}\right) ^n\), where \(D_2\) is an undetermined constant. Then, utilizing the Table 2.3 presented in the monograph by Elaydi (2005), a particular solution of Eq. (32) can be given by

$$\begin{aligned} Q_{n,1}^{*(\mathrm{part})}(s)= & {} \sum \limits _{j=1}^b\frac{k_j\left( \omega _j^n-a^*(s)\sum \limits _{i=1}^bg_i\omega _j^{n-i}\right) }{s-\mu _1(1-\omega _j)}\nonumber \\&+\sum \limits _{j=1}^b\frac{\phi _j\eta \left( r_j^n-a^*(s)\sum \limits _{i=1}^bg_ir_j^{n-i}\right) }{s-\mu _1(1-r_j)}\nonumber \\&\left[ \frac{1}{(\mu _1 -\mu _0)(1 -r_j) -\eta } -\frac{1}{s -\eta -\mu _0(1 - r_j)}\right] \nonumber \\= & {} \sum \limits _{j=1}^{b} \frac{k_j \left( \omega _j^n - a^*(s)\sum \limits _{i=1}^bg_i\omega _j^{n-i}\right) }{s - \mu _1(1 - \omega _j)}\nonumber \\&+ \sum \limits _{j=1}^b \frac{\phi _j\eta \left( r_j^n-a^*(s)\sum \limits _{i=1}^bg_ir_j^{n-i}\right) }{\left[ (\mu _1 - \mu _0)(1 - r_j) - \eta \right] \left[ s - \eta - \mu _0(1 - r_j)\right] }. \end{aligned}$$
(33)

Thus, for \(n\ge b\), the general solution of Eq. (32) can be written as \(Q_{n,1}^*(s)=Q_{n,1}^{*(\mathrm{part})}(s)+Q_{n,1}^{*(\hom )}(s)\). Summing over all permissible n from b to \(\infty\) and taking the limit as \(s\rightarrow 0\), the formula \(\sum \nolimits _{n=b}^\infty Q_{n,1}^*(0)=\sum \nolimits _{n=b}^\infty Q_{n,1}\le 1\) clearly holds. This means that the undetermined constant \(D_2=0\). Otherwise, the limit of \(\sum \nolimits _{n=b}^\infty D_2\left( 1- \frac{s}{\mu _2}\right) ^n\), as s approaches 0, is infinity. Therefore, the solution of Eq. (32) takes the below form

$$\begin{aligned}Q_{n,1}^*(s)& = \sum \limits _{j=1}^b \frac{k_{j} \left( \omega _j^n - a^*(s)\sum \limits _{i=1}^bg_i\omega _j^{n-i}\right) }{s - \mu _1(1 - \omega _j)}\nonumber \\&\quad +\sum \limits _{j=1}^{b} \frac{\phi _j\eta \left( r_j^n-a^*(s)\sum \limits _{i=1}^bg_ir_j^{n-i}\right) }{\left[ (\mu _0 - \mu _1)(1 - r_j) - \eta \right] \left[ s - \eta - \mu _0(1 - r_j)\right] }, \quad n\ge b. \end{aligned}$$
(34)

We now find the condition under which the expression for \(Q_{n,1}^*(s)\) presented in Eq. (34) also holds when \(1\le n\le b-1\). Insert Eqs. (28) and (32) into Eqs. (11) and (12), respectively. By comparing the last term of the right hand side of Eqs. (11) and (12), we need to imposes the following restrictions on the constants \(k_j\) and \(\phi _j\).

$$\begin{aligned} \sum \limits _{j=1}^bk_j\sum \limits _{i=n+1}^bg_i\omega _j^{n-i}+\eta \sum \limits _{j=1}^b\frac{\eta \phi _j}{\left[ (\mu _1 - \mu _0)(1 - r_j) - \eta \right] }\sum \limits _{i=n+1}^bg_ir_j^{n-i}=0, \quad 1\le n\le b-1. \end{aligned}$$
(35)

By putting \(n=b-1,b-2,\ldots ,1\) in Eq. (35) and noting that \(g_b\ne 0\), Eq. (35) can be conveniently written in the form of a linear equation with 2b variables, i.e., \(k_1\), \(k_2\), \(\ldots\), \(k_b\), \(\phi _1\), \(\phi _2\), \(\ldots\), \(\phi _b\).

$$\begin{aligned} \left\{ \begin{array}{l} \sum \limits _{j=1}^b\displaystyle \frac{k_j}{\omega _j}+\sum \limits _{j=1}^b\displaystyle \frac{\phi _j\eta }{\left[ (\mu _1-\mu _0)(1-r_j)-\eta \right] r_j}=0,\\ \sum \limits _{j=1}^b\displaystyle \frac{k_j}{\omega _j^2}+\sum \limits _{j=1}^b\displaystyle \frac{\phi _j\eta }{\left[ (\mu _1-\mu _0)(1-r_j)-\eta \right] r_j^2}=0,\\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ \sum \limits _{j=1}^b\displaystyle \frac{k_j}{\omega _j^{b-2}}+\sum \limits _{j=1}^b\displaystyle \frac{\phi _j\eta }{\left[ (\mu _1-\mu _0)(1-r_j)-\eta \right] r_j^{b-2}}=0,\\ \sum \limits _{j=1}^b\displaystyle \frac{k_j}{\omega _j^{b-1}}+\sum \limits _{j=1}^b\displaystyle \frac{\phi _j\eta }{\left[ (\mu _1-\mu _0)(1-r_j)-\eta \right] r_j^{b-1}}=0.\\ \end{array}\right. \end{aligned}$$
(36)

In other words, for \(1\le n\le b-1\) and \(n\ge b\), if the above Eq. (36) holds, \(Q_{n,1}^*(s)\) has the uniform expression as follows:

$$\begin{aligned}Q_{n,1}^*(s)&=\sum \limits _{j=1}^b\frac{k_j\left( 1-a^*(s)G(\omega _j^{-1})\right) \omega _j^n}{s-\mu _1(1-\omega _j)}\nonumber \\&\quad +\sum \limits _{j=1}^b\frac{\phi _j\eta \left( 1-a^*(s)G(r_j^{-1})\right) r_j^n}{\left[ (\mu _1 - \mu _0)(1 - r_j) - \eta \right] \left[ s - \eta - \mu _0(1 - r_j)\right] }, \quad n\ge 1. \end{aligned}$$
(37)

Setting \(s=\beta\) and using Eqs. (31) and (37) in Eq. (10), we can obtain another linear equation in the same 2b variables

$$\begin{aligned}&\sum \limits _{j=1}^bk_j+\eta \sum \limits _{j=1}^b\frac{\phi _j}{(\mu _1 - \mu _0)(1 - r_j)-\eta }-\mu _1\sum \limits _{j=1}^b \frac{k_j\left( 1 - a^*(\beta )G(\omega _j^{-1})\right) \omega _j}{\beta - \mu _1(1 - \omega _j)}\nonumber \\&\quad -\mu _1\sum \limits _{j=1}^b\frac{\phi _j\eta \left( 1 - a^*(\beta )G(r_j^{-1})\right) r_j}{\left[ (\mu _1 - \mu _0)(1 - r_j)-\eta \right] \left[ \beta - \eta - \mu _0(1 - r_j)\right] }=0. \end{aligned}$$
(38)

By summing over all possible n from 0 to \(\infty\) in Eq. (16) and employing Eqs. (21) and (31), we can further derive a relationship for \(\phi _j\) and \(k_j\), \(j=1,2,\ldots ,b\).

$$\begin{aligned} \sum \limits _{j=1}^b\frac{\phi _j(\mu _1-\mu _0)}{(\mu _1-\mu _0)(1-r_j)-\eta }+\sum \limits _{j=1}^b\frac{k_j}{1-\omega _j}=\lambda . \end{aligned}$$
(39)

So far, by the use of Eqs. (27), (36), (38) and (39), we have established a system of 2b linear equations in 2b variables which can be solved to obtain the constants \(\phi _j\)’s and \(k_j\)’s, \(j=1,2,\ldots ,b\). Once the arbitrary constants are determined by solving the linear algebraic equations, the stationary queue-length distributions at pre-arrival and arbitrary epochs are given, respectively, by

$$\begin{aligned}&\left\{ \begin{array}{l} Q_{n,0}^- = \displaystyle \frac{1}{\lambda }Q_{n,0}(0)=\frac{1}{\lambda }\sum \limits _{j=1}^b\phi _jr_j^n, \quad n\ge 0,\\ Q_{n,1}^- = \displaystyle \frac{1}{\lambda }Q_{n,1}(0)=\frac{1}{\lambda }\left( \sum \limits _{j=1}^bk_j\omega _j^n+ \eta \sum \limits _{j=1}^b\frac{\phi _j}{(\mu _1-\mu _0)(1-r_j)-\eta }r_j^n\right) ,n\ge 0,\end{array}\right. \end{aligned}$$
(40)
$$\begin{aligned}&\left\{ \begin{array}{l} Q_{n,0} = Q_{n,0}^*(0) = \displaystyle \sum \limits _{j=1}^b\frac{\phi _j\left[ G(r_j^{-1}) - 1\right] }{\eta +\mu _0(1 - r_j)}r_j^n, \quad n\ge 1,\\ Q_{n,1} = Q_{n,1}^*(0) = \displaystyle \sum \limits _{j=1}^b\frac{k_j\left[ G(\omega _j^{-1}) - 1\right] \omega _j^n}{\mu _1(1 - \omega _j)} + \sum \limits _{j=1}^b\frac{\phi _j\eta \left[ G(r_j^{-1}) - 1\right] r_j^n}{\left[ (\mu _1 - \mu _0)(1 - r_j) - \eta \right] \left[ \eta +\mu _0(1 - r_j)\right] }, \quad n\ge 1. \end{array}\right. \end{aligned}$$
(41)

Remark 1

Our queueing model is a generalization of the classical M/M/1 queue. More precisely, such a model reduces to M/M/1 queue when \(\eta \rightarrow 0\), \(\beta \rightarrow \infty\), \(\mu _0=\mu _1\), \(g_1=1\) and \(a^*(s)=\frac{\lambda }{s+\lambda }\). For this case \(b=1\), thus the single characteristic root inside the unit circle is \(r_1=\omega _1=\lambda /\mu _1\). Hence, we may compute the probability that an arriving customer finds an empty system (denoted as \(Q_0^-\)) from Eq. (40) and obtain \(Q_0^-=Q_{0,0}^-+Q_{0,1}^-=\frac{\phi _1+k_1}{\lambda }\). On the other hand, substituting \(r_1=\omega _1=\lambda /\mu _1\) into Eq. (39), we can find that \(\frac{\phi _1+k_1}{\lambda }\) satisfies the relationship \(\frac{\phi _1+k_1}{\lambda }=\left( 1-\frac{\lambda }{\mu _1}\right) =(1-\rho )=Q_0^-\). The relationship also implies that \(Q_n^-= Q_{n,0}^-+Q_{n,1}^-=\frac{\phi _1+k_1}{\lambda }r_1^n=(1-\rho )\rho ^n\), \(n=1,2,\ldots\), where \(Q_n^-\) represents the probability that there are n customers in the system just before the arrival of a customer. Therefore, according to the PASTA property (Poisson Arrivals See Time Averages), we get exactly the same results that have been reported in the existing literature on queueing theory (see Gross and Harris 1985).

Furthermore, setting \(s=0\) in Eq. (10), we obtain

$$\begin{aligned} Q_{0,1}= & {}\, Q_{0,1}^*(0)=\frac{1}{\beta }\left[ \mu _1Q_{1,1}^*(0)-Q_{0,1}(0)\right] \nonumber \\= & {}\, \frac{\mu _1}{\beta }\left( \sum \limits _{j=1}^b\frac{k_j\left[ G(\omega _j^{-1})-1\right] \omega _j}{\mu _1(1-\omega _j)} \right. \nonumber \left. +\sum \limits _{j=1}^b\frac{\phi _j\eta \left[ G(r_j^{-1})-1\right] r_j}{\left[ (\mu _1-\mu _0)(1-r_j)-\eta \right] \left[ \eta +\mu _0(1-r_j)\right] }\right) \nonumber \\&-\frac{1}{\beta }\left( \sum \limits _{j=1}^bk_j+\eta \sum \limits _{j=1}^b\frac{\phi _j}{(\mu _1-\mu _0)(1-r_j)-\eta }\right) . \end{aligned}$$
(42)

With the help of the normalizing condition \(\sum \nolimits _{n=0}^\infty Q_{n,0}+\sum \nolimits _{n=0}^\infty Q_{n,1}=1\), we may further obtain

$$\begin{aligned} Q_{0,0}= & {}\, 1 - \sum \limits _{j=1}^b\frac{\phi _jr_j\left[ G(r_j^{-1}) - 1\right] }{\eta (1 - r_j)+\mu _0(1 - r_j)^2} - \sum \limits _{j=1}^b\frac{k_j\omega _j\left[ G(\omega _j^{-1}) - 1\right] }{\mu _1(1-\omega _j)^2}\nonumber \\&- \sum \limits _{j=1}^b\frac{\phi _jr_j\eta \left[ G(r_j^{-1})-1\right] }{\left[ (\mu _1 - \mu _0)(1 - r_j)^2 - \eta (1 - r_j)\right] \left[ \eta +\mu _0(1 - r_j)\right] }\nonumber \\&-\frac{\mu _1}{\beta }\left( \sum \limits _{j=1}^b\frac{k_j\left[ G(\omega _j^{-1})-1\right] \omega _j}{\mu _1(1-\omega _j)}\right. \nonumber \\&\left. + \sum \limits _{j=1}^b\frac{\phi _j\eta \left[ G(r_j^{-1})-1\right] r_j}{\left[ (\mu _1-\mu _0)(1-r_j)-\eta \right] \left[ \eta +\mu _0(1-r_j)\right] }\right) \nonumber \\&+\frac{1}{\beta }\left( \sum \limits _{j=1}^bk_j+\eta \sum \limits _{j=1}^b\frac{\phi _j}{(\mu _1-\mu _0)(1-r_j)-\eta }\right) \end{aligned}$$
(43)

This completes the analysis of queue-length distribution at different epochs.

5 Sojourn time for an arbitrary customer

The sojourn time \(T_A\) is the total time that an arbitrary customer in an arriving batch spends in the system until it departs from the system. Using the pre-arrival epoch probabilities \(Q_{n,0}^-\) and \(Q_{n,1}^-\) that we have derived in Sect. 4, we will investigate the Laplace–Stieltjes transform and the expectation of an arbitrary customer’s sojourn time in this section. For this purpose, we introduce a tagged customer who may arrive at a random position in the queue. Clearly, it may be seen that a tagged customer arrival may belong to one of the following cases:

Case 1. A batch containing the tagged customer arrives at the system during the normal working period and finds n customers already present in the system. Meanwhile, the number of customers that arrive in the same batch as the tagged customer, but enter service before the tagged customer is l \((l=0,1,\ldots ,b-1)\). To discuss the sojourn time of the tagged customer, this case can further be divided into two subcases: (i) The time until the random partial breakdown of the server is no less than the total service time of \(n+l+1\) customers. That is to say, the tagged customer completes its service and leaves the system in the normal working period; (ii) There are only m \((m=0,1,\ldots ,n+l)\) service completions during the normal working period. In other words, the tagged customer leaves the system when the server undergoes in the defective state.

Case 2. An arriving batch sees the state of the system is (n, 1), \(n\ge 0\), and the \((l+1)\)th customer in this batch is the tagged customer. Then, the sojourn time of the tagged customer equals the total customers’ service times ahead of him plus his service time. Since the server is defective, these services are only provided with the low service rate \(\mu _1\).

Let \(W_{A}(t)\) be defined as the probability distribution function of \(T_{A}\), and \(g_l^-\) denotes the probability of l number of customers ahead of a randomly selected tagged customer within the batch. From Burke (1975) and Chaudhry and Templeton (1983), \(g_l^-\) is given by \(g_l^-=\frac{1}{\bar{g}}\sum \nolimits _{j=l+1}^{\infty }g_j\). Based on the above different cases, we have, from the theorem of total probability,

$$\begin{aligned}W_{A}(t) &= \Pr \left\{ T_{A}\le t\right\} \nonumber \\& = \sum \limits _{n=0}^\infty Q_{n,0}^-\left[ \sum \limits _{l=0}^{b-1}g_l^-\left( \Pr \left\{ \left. T_{A}=\sum \limits _{h=1}^{n+l+1}S_h\le t\right| \sum \limits _{h=1}^{n+l+1}S_h\le L\right\} \Pr \left\{ \sum \limits _{h=1}^{n+l+1} S_h\le L\right\} \right. \right. \nonumber \\&\quad \left. \left. +\sum \limits _{m=0}^{n+l} \Pr \left\{ \left. T_{A} = L+\sum \limits _{h=m+1}^{n+l+1}{\tilde{S}}_h \le t\right| \sum \limits _{h=1}^m S_{h} \le L< \sum \limits _{h=1}^{m+1} S_h \right\} \right. \right. \nonumber \\&\quad \left. \left. \Pr \left\{ \sum \limits _{h=1}^m S_h \le L < \sum \limits _{h=1}^{m+1} S_h\right\} \right) \right] \nonumber \\&\quad +\sum \limits _{n=0}^\infty Q_{n,1}^-\sum \limits _{l=0}^{b-1}g_l^-\Pr \left\{ T_{A}=\sum \limits _{h=1}^{n+l+1}{\tilde{S}}_h\le t\right\} \nonumber \\& = \sum \limits _{n=0}^\infty Q_{n,0}^-\left[ \sum \limits _{l=0}^{b-1} g_l^-\left( \int _0^t\frac{\mu _0(\mu _0x)^{n+l}}{(n+l)!}e^{-(\mu _0+\eta )x}\mathrm{d}x\right. \right. \nonumber \\&\quad \left. \left. + \sum \limits _{m=0}^{n+l}\int _0^t\frac{(\mu _0x)^m}{m!}e^{-\mu _0x}\eta e^{-\eta x}\left( 1 - e^{-\mu _1(t-x)} \sum \limits _{i=0}^{n+l-m}\frac{(\mu _1(t-x))^i}{i!}\right) \mathrm{d}x\right) \right] \nonumber \\&\quad +\sum \limits _{n=0}^\infty Q_{n,1}^-\sum \limits _{l=0}^{b-1}g_l^-\left[ 1-e^{-\mu _1t}\sum \limits _{i=0}^{n+l}\frac{(\mu _1t)^i}{i!}\right] . \end{aligned}$$
(44)

The Laplace–Stieltjes transform of the distribution of \(T_A\) is given by

$$\begin{aligned} W_{A}^*(s)= & {} \int _0^\infty e^{-st}\mathrm{d}W_{A}(t)\nonumber \\= & {} \sum \limits _{n=0}^\infty Q_{n,0}^- \left[ \sum \limits _{l=0}^{b-1} g_l^- \left( \left( \frac{\mu _0}{s+\mu _0+\eta }\right) ^{n+l+1}\right. \right. \nonumber \\&\left. \left. + \sum \limits _{m=0}^{n+l}\frac{\eta \mu _0^m}{(s+\mu _0+\eta )^{m+1}}\left( \frac{\mu _1}{s+\mu _1}\right) ^{n+l+1-m}\right) \right] \nonumber \\&+\sum \limits _{n=0}^\infty Q_{n,1}^- \sum \limits _{l=0}^{b-1} g_l^- \left( \frac{\mu _1}{s+\mu _1}\right) ^{n+l+1}. \end{aligned}$$
(45)

Hence, the first and second moments of \(T_A\) may be found from the Laplace–Stieltjes transform as

$$\begin{aligned} \mathrm{E}\left[ T_{A}\right]= & {} \left. -\frac{\mathrm{d}}{\mathrm{d}s}W_A^*(s)\right| _{s=0}\nonumber \\= & {} \sum \limits _{n=0}^\infty Q_{n,0}^- \left[ \sum \limits _{l=0}^{b-1} g_l^- \left( \frac{(n +l+ 1)\mu _0^{n+l+1}}{(\mu _0+\eta )^{n +l+ 2}}\right. \right. \nonumber \\&\left. \left. +\sum \limits _{m=0}^{n+l}\frac{(m+1)\eta \mu _0^m}{(\mu _0+\eta )^{m+2}}+\frac{\eta \mu _0^m}{(\mu _0+\eta )^{m+1}}\frac{(n+l+1 - m)}{\mu _1}\right) \right] \nonumber \\&+\sum \limits _{n=0}^\infty Q_{n,1}^-\sum \limits _{l=0}^{b-1}g_l^-\frac{(n+l+1)}{\mu _1}, \end{aligned}$$
(46)
$$\begin{aligned} \mathrm{E}\left[ T_A^2\right]= & {} \left. \frac{\mathrm{d}^2}{\mathrm{d}s^2}W_A^*(s)\right| _{s=0}\nonumber \\= & {} \sum \limits _{n=0}^\infty Q_{n,0}^-\left[ \sum \limits _{l=0}^{b-1}g_l^-\left( \frac{(n+l+1)(n+l+2)\mu _0^{n+l+1}}{(\mu _0+\eta )^{n+l+3}}\right. \right. \nonumber \\&\left. \left. + \sum \limits _{m=0}^{n+l}\left( \frac{(m+1)(m+2)\eta \mu _0^m}{(\mu _0+\eta )^{m+3}}\right. \right. \right. \nonumber \\&\left. \left. \left. +\frac{2(m+1)(n+l+1-m)\eta \mu _0^m}{(\mu _0+\eta )^{m+2}\mu _1}+\frac{(n+l+1-m)(n+l+2-m)}{(\mu _0+\eta )^{m+ 1}\mu _1^2}\right) \right) \right] \nonumber \\&+\sum \limits _{n=0}^\infty Q_{n,1}^-\sum \limits _{l=0}^{b-1}g_l^-\frac{(n+l+1)(n+l+2)}{\mu _1^2}. \end{aligned}$$
(47)

From the numerical examples presented in the next section, we will see that Eq. (46) can provide us an effective way to validate the correctness of our theoretical analysis results. Moreover, using Eqs. (46) and (47) we can compute the variance of \(T_A\) as \(\mathrm{Var}(T_A)=\mathrm{E}\left[ T_A^2\right] -\mathrm{E}^2\left[ T_{A}\right]\).

6 Numerical illustrations

To demonstrate the working schemes of the difference equation approach based on the right shift operator, we first describe the solution algorithm for calculating the steady-state probabilities \(Q_{n,0}^-\), \(Q_{n,1}^-\), \(Q_{n,0}\) and \(Q_{n,1}\), for \(n\ge 0\). Given the values of \(\mu _0\), \(\mu _1\), \(\eta\), \(\beta\), the Laplace–Stieltjes transform expression of the inter-batch arrival time \(a^*(s)\) and the probability mass function \(g_i=\Pr \left\{ X=i\right\}\), \(i=1,2,\ldots ,b\), the steps of the solution algorithm are stated as follows:

  • Step 1: Find the roots of the following two characteristic equations \(z^b-a^*(\eta +\mu _0-\mu _0z)\sum \nolimits _{i=1}^bg_iz^{b-i}=0\) and \(z^b-a^*(\mu _1-\mu _1z)\sum \nolimits _{i=1}^bg_iz^{b-i}=0\) inside the unit circle, respectively. Denote these roots as \(r_j\) and \(\omega _j\), \(j=1,2,\ldots ,b\).

  • Step 2: Insert these roots directly into Eqs. (27), (36), (38) and (39), and solve a system of linear equations to find the values of the unknown constants \(\phi _j\) and \(k_j\), \(j=1,2,\ldots ,b\).

  • Step 3: Substituting the values of \(\phi _j\) and \(k_j\) into Eq. (40), find \(Q_{n,0}^-\) and \(Q_{n,1}^-\), for \(n\ge 0\).

  • Step 4: Inserting the values of \(\phi _j\) and \(k_j\) into Eqs. (41), (42) and (43), compute \(Q_{n,0}\) and \(Q_{n,1}\), for \(n\ge 0\).

All the calculations are performed on a PC having Corei7 processor at 3.20 gigahertz with 16 gigabytes RAM using Mathematica and Matlab software packages. We use Mathematica software to find the roots of the associated characteristic equations, and then write a Matlab code to solve a linear system of equations in 2b variables. Next, to illustrate the solution algorithm, we provide three numerical examples where the inter-batch arrival time distributions are 2-stage Erlang, uniform and deterministic, respectively. A variety of numerical results have been presented in self-explanatory tables and graphs. The notations used in these tables are the same as those defined earlier in the previous sections except \(\mathrm{E}\left[ T_{A}\right] _{\mathrm{Little}}\), which denotes the average sojourn time of an arbitrary customer evaluated through Little’s formula.

Example 1

Consider the E\(_2^X\)/M/1 queueing system with fault tolerance capabilities. The 2-stage Erlang distribution is made up of two independent and identical exponential stages, each with mean 2.5. In this case, we have \(a^*(s)=\left( \frac{0.4}{s+0.4}\right) ^2\). The number of customers (X) belonging to each arrival has the following probability mass function \(g_i=\Pr \left\{ X=i\right\} =\frac{0.55(1-0.55)^{i-1}}{1-(1-0.55)^{10}}\) (\(i=1,2,\ldots ,10\)) with mean value \({\bar{g}}=1.814776\). For computation purpose, we fix the other parameters as \(\mu _0=0.7\), \(\mu _1=0.4\), \(\eta =0.005\) and \(\beta =0.2\). Table 1 displays the the roots of the characteristic equations inside the unit circle, where \(\mathbf{i}\) is the imaginary unit. The corresponding constants \(\phi _j\) and \(k_j\) for \(j=1,2,\ldots ,10\) are determined by solving a systems of linear equations with twenty variables in computing software. The calculation results are reported in Table 2.

Table 1 The roots of the characteristic equations with modulus less than one in Example 1
Full size table
Table 2 The values of \(\phi _j\) and \(k_j\) for \(j=1,2,\ldots ,10\) in Example 1
Full size table

With the known values of \(\phi _j\), \(k_j\), \(r_j\) and \(\omega _j\), Table 3 also gives a few queue-length distributions at pre-arrival and arbitrary epochs. Utilizing the data presented in Table 3, an effective approach is provided to verify the correctness of our numerical as well as analytical results. Actually, there are two different ways to get the average sojourn time for an arbitrary customer. One way is to substitute \(Q_{n,0}^-\) and \(Q_{n,1}^-\) into Eq. (46) and calculate \(\mathrm{E}\left[ T_{A}\right]\) directly. The other is to apply Little’s formula to obtain \(\mathrm{E}\left[ T_{A}\right] =L_s/{\bar{g}}\lambda\), where \(L_s=\sum \nolimits _{n=1}^\infty n(Q_{n,0}+Q_{n,1})\). The results from numerical computation (see the bottom of Table 3) indicate that \(\mathrm{E}\left[ T_{A}\right]\) evaluated through Eq. (46) exactly matches with the one obtained from Little’s formula. It also implies that the theoretical analysis and numerical experiments performed in this paper is valid and reliable.

Table 3 Steady-state queue-length distributions at pre-arrival and arbitrary epochs in Example 1
Full size table

In the first example, we consider the case when inter-arrival times of groups have Erlangian distribution of order 2. We note that such an arrival process is a particular case of the batch Markovian arrival process (BMAP). The corresponding numerical results can be much easier obtained by using the well-known matrix geometric method. To further demonstrate the universality of the proposed method, some other examples with an inter-batch arrival time that does not belong to the class of PH distribution are given below.

Example 2

Consider the U\(^X\)/M/1 queue with fault tolerance capabilities, where the inter-batch arrival times are independent random variables, each distributed uniformly on interval 0 to \(2/\lambda\). If we set \(\lambda =0.2\), the uniform distribution has the Laplace–Stieltjes transform \(a^*(s)=\frac{1}{10s}(1-\mathrm{e}^{-10s})\). The maximum batch size is \(b=12\), and take the probability mass function of batch size to be \(g_i=\Pr \left\{ X=i\right\} =\frac{\mathrm{e}^{-2}2^i}{i!\sum \nolimits _{n=1}^b\frac{\mathrm{e}^{-2}2^n}{n!}}\), \(i = 1,2,\ldots ,12\) with mean value \({\bar{g}}=1.930825\). Since \(a^*(s)\) is a transcendental function, the corresponding characteristic equations cannot be directly solved by using the standard Mathematica commands. For the purpose of finding the roots of the characteristic equations, we wish to approximate \(a^*(s)\) by means of a rational approximation \({\mathbb {P}}_1(s)/{\mathbb {P}}_2(s)\), where \({\mathbb {P}}_1(s)\) and \({\mathbb {P}}_2(s)\) are polynomials of degree \(m_1\) and \(m_2\) respectively. It is well known that the Pad\(\acute{\mathrm{e}}\) approximation is a particular and classical type of rational fraction approximation. Many practical applications have proven that it is the best approximation of a function by a rational function of a given order. In this example, we shall use the so-called Pad\(\acute{\mathrm{e}}\) rational approximation of degree (15, 16) to approximate \(a^*(s)\)

$$\begin{aligned}&a^*(s)=\frac{{\mathbb {P}}_1(s)}{{\mathbb {P}}_2(s)}\\&\quad =\frac{1+\frac{350s^2}{93}+\frac{3250s^4}{899}+\frac{687500s^6}{509733}+\frac{343750 s^8}{1529199}+\frac{312500s^{10}}{18423207}+\frac{7812500s^{12}}{15088606533}+\frac{78125000s^{14}}{18061062020001}}{\left( \begin{array}{c} 1+5s+\frac{375s^2}{31}+\frac{1750s^3}{93}+\frac{56875s^4}{2697}+\frac{16250s^5}{899}+\frac{893750s^6}{72819}+\frac{3437500s^7}{509733}\\ +\frac{171875s^8}{56637}+\frac{1718750s^9}{1529199}+\frac{1718750 s^{10}}{5024511}+\frac{1562500s^{11}}{18423207}+\frac{19531250s^{12}}{1160662041}\\ +\frac{39062500s^{13}}{15088606533}+\frac{195312500s^{14}}{668928222963}+\frac{390625000 s^{15}}{18061062020001}+\frac{244140625s^{16}}{307038054340017}\\ \end{array}\right) }. \end{aligned}$$

Here, calculations with Pad\(\acute{\mathrm{e}}\) approximant of \(a^*(s)\) are straightforward and can be performed with Mathematica command “PadeApproximant”. How the choice of Pad\(\acute{\mathrm{e}}\) (\(m_1\), \(m_2\)) affects the accuracy of numerical results and how one can trade off between computation-time and accuracy is discussed in detail in the work of Singh et al. (2014). By the fixed values of certain parameters \(\mu _0\), \(\mu _1\), \(\eta\) and \(\beta\) as 0.75, 0.5, 0.003 and 0.1 respectively, we present the numerical results for the roots of the characteristic equations inside the unit circle in Table 4.

Table 4 The roots of the characteristic equations with modulus less than one in Example 2
Full size table

Substituting these roots into Eqs. (27), (36), (38) and (39), and solving a simultaneous set of twenty-four linear equations, Table 5 gives the numercal results of \(\phi _j\) and \(k_j\) for \(j=1,2,\ldots ,12\).

Table 5 The values of \(\phi _j\) and \(k_j\) for \(j=1,2,\ldots ,12\) in Example 2
Full size table

The summary of the calculations for the queue-length distributions at pre-arrival and arbitrary epochs is shown in Table 6. At the same time, the expected sojourn time for an arbitrary customer estimated in two different ways is also summarized at the bottom of Table 6. We may see that the numerical experiments verify our theoretical results and show their correctness once again.

Table 6 Steady-state queue-length distributions at pre-arrival and arbitrary epochs in Example 2
Full size table

Example 3

Consider the D\(^X\)/M/1 queue with a fault-tolerant server, in which the batch arrivals are equally spaced in time. For this inter-batch arrival time distribution \(a^*(s)=\mathrm{e}^{-\frac{s}{\lambda }}\), here we take \(\lambda =0.2\). Now, let us conduct the numerical experiment with the following parameters: \(\mu _0=0.8\), \(\mu _1=0.6\), \(\eta =0.0025\) and \(\beta =0.15\). Additionally, the corresponding numerical results were obtained by assuming that the batch size distribution has a p.g.f. \(G(z)=0.25z+0.5z^2+0.1z^4+0.1z^6+0.05z^8\). This suggests that the batch size can be either 1, 2, 4, 6, or 8 with \(25\%\), \(50\%\), \(10\%\), \(10\%\) and \(5\%\) probabilities, respectively. Since the deterministic inter-batch arrival time does not have a rational Laplace–Stieltjes transform, Mathematica software package cannot solve the characteristic equations (transcendental equations) directly. Through the Pad\(\acute{\mathrm{e}}\) approximation of degree (8, 9), we also approximate the Laplace–Stieltjes transform of the inter-batch arrival time distribution \(\mathrm{e}^{-5s}\) with a rational function of the type \({\mathbb {P}}_1(s)/{\mathbb {P}}_2(s)\):

$$\begin{aligned}&\mathrm{e}^{-5s}=\frac{{\mathbb {P}}_1(s)}{{\mathbb {P}}_2(s)}\\&\quad =\frac{1 - \frac{40s}{17}+\frac{175s^2}{68} - \frac{175s^3}{102}+\frac{625s^4}{816} - \frac{625s^5}{2652}+\frac{3125s^6}{63648} - \frac{15625s^7}{2450448}+\frac{15625s^8}{39207168}}{1+\frac{45s}{17}+\frac{225s^2}{68}+\frac{175s^3}{68}+\frac{375s^4}{272}+\frac{1875s^5}{3536}+\frac{3125s^6}{21216}+ \frac{15625s^7}{544544}+\frac{15625s^8}{4356352}+\frac{78125s^9}{352864512}}. \end{aligned}$$

Letting \(s=0.8025-0.8z\) and \(s=0.6-0.6z\) in the above expression, respectively, and putting them into the characteristic equations, Table 7 gives all distinct roots that are found within the contour of a unit circle \(|z|=1\).

Table 7 The roots of the characteristic equations with modulus less than one in Example 3
Full size table

The unknown constants \(\phi _j\) and \(k_j\) for \(j=1,2,\ldots ,8\) can be found in the same manner as described earlier. Table 8 displays all the calculation results.

Table 8 The values of \(\phi _j\) and \(k_j\) for \(j=1,2,\ldots ,8\) in Example 3
Full size table

Using Eqs. (40), (41), (42) and (43), we compute the probability distributions of the queue length at two different epochs, and the numerical results are listed in Table 9. It is also found that \(\mathrm{E}\left[ T_A\right]\) matches exactly with the mean sojourn time calculated using Little’s law.

Table 9 Steady-state queue-length distributions at pre-arrival and arbitrary epochs in Example 3
Full size table

Example 4

In this example, the computer software, e.g., Mathematica and Matlab, are used to compare three configurations in terms of their \(E\left[ T_A\right]\) and \(L_s\) for three different inter-batch arrival time distributions: 2-stage Erlang, uniform and deterministic. We first perform a comparison for the average sojourn time of an arbitrary customer using the assumption that these distributions have the same mean 5 but different standard deviations. We choose \(\mu _0=0.9\), \(\mu _1=0.75\), \(\eta =0.0025\), and suppose X is a discrete uniform random variable on the consecutive integers 1, 2, \(\ldots\), 6, so that the traffic intensity \(\rho =0.883333\). At the same time, to evaluate the impact of the repair rate \(\beta\) on the value of \(\mathrm{E}\left[ T_A\right]\), we vary the values of \(\beta\) from 0.05 to 0.25 and draw the plot of \(\mathrm{E}\left[ T_A\right]\) as a function of \(\beta\). Figure 1(a) depicts that \(\mathrm{E}\left[ T_A\right]\) decreases as \(\beta\) increases. That is to say, moderate shortening the sojourn time of an arbitrary customer can be achieved by choosing a higher repair rate. On the other hand, we also observe that the expected sojourn time is larger for 2-stage Erlang distribution as compared to uniform and deterministic distributions. We think in most of the cases, by comparing \(\mathrm{E}\left[ T_A\right]\) in terms of three different distributions of the inter-batch arrival time usually yields \(\mathrm{E}\left[ T_A\right] _{E_2}>\mathrm{E}\left[ T_A\right] _{U}>\mathrm{E}\left[ T_A\right] _{D}\). This is due to the fact that the standard deviation of the deterministic distribution equals zero. In Figure 1(b), under the same parameter settings, it can be seen that the average queue length in the case of 2-stage Erlang inter-batch arrival time distribution with a higher standard deviation is larger than the one with lower standard deviations. Again deterministic distribution with zero standard deviation yields the lowest average queue length. Such results indicate that the inter-batch arrival time plays a significant role in determining the performance of the queueing system.

Fig. 1
figure 1

Effect of \(\beta\) on \(\mathrm{E}\left[ T_A\right]\) and \(L_s\) for various inter-batch arrival time distributions

Full size image

Example 5

In this example, we perform a comparative analysis on \(\mathrm{E}[T_A]\) and \(L_s\) based on changes in specific random arrival batch size distributions and assume that the inter-batch arrival times have a common 3-phase hyperexponential distribution, whose density and Laplace transform are given by

$$\begin{aligned}&a(t)=0.2\cdot \frac{1}{10}e^{-\frac{1}{10}t}+0.5\cdot \frac{1}{5}e^{-\frac{1}{5}t}+0.3\cdot \frac{2}{5}e^{-\frac{2}{5}t}, \quad t>0,\\&a^*(s)=\left( \frac{0.2\times 0.1}{0.1+s}\right) +\left( \frac{0.5\times 0.2}{0.2+s}\right) +\left( \frac{0.3\times 0.4}{0.4+s}\right) . \end{aligned}$$

A k-phase hyperexponential distribution is frequently used in queueing theory to model the distribution of the superposition of k independent events. For instance, the arrival of different types of customer to a single queueing station is often modeled as a hyperexponential distribution. To demonstrate the performance evaluation, we consider the following three batch size distributions:

Case 1: Batch size X follows the discrete uniform distribution on the interval \(\left[ 1,2,\ldots ,16\right]\).

Case 2: The batch size distribution has the probability mass function: \(g_4=0.25\), \(g_8=0.25\), \(g_{10}=0.25\), and \(g_{12}=0.25\).

Case 3: The arriving batch size follows a 6-8-12 distribution with probability mass function \(g_6=0.25\), \(g_8=0.5\), and \(g_{12}=0.25\).

All these distributions are characterized by the average batch size equal to 8.5. However, these are qualitatively different in that they have different variances, the variances of above probability distributions are 21.25, 8.75 and 4.75, respectively. The numerical experiment has been done by fixing other system parameters as \(\mu _0=2.5\), \(\mu _1=2\), \(\eta =0.001\) and \(\beta =0.08\). We observe that \(E[T_{{\text{A}}} ]\) and \(L_s\) decrease as the variance of the batch size distribution decreases, namely \(\mathrm{E}[T_A]_{\mathrm{(case 1)}}=9.384734>\mathrm{E}[T_A]_{\mathrm{(case 2)}}=8.329050>\mathrm{E}[T_A]_\mathrm{(case 3)}=7.990203\) and \(L_{s\mathrm{(case 1)}}=15.194332>L_{s\mathrm{(case 2)}}=13.485130>L_{s\mathrm{(case 3)}}=12.936519\). So, we can conclude that the variance of batch size has obvious impact on performance metrics like average system size and average sojourn time.

7 Conclusions

In order to mitigate the severe potential consequences of system failure, fault-tolerant operating has become a critical attribute of the manufacturing system. In this paper, we have developed a GI\(^X\)/M/1 queue with a fault-tolerant server to study the behavior of key performance indicators for such a system. The mathematical analysis of the queueing model is carried out by employing a combination of two methods. One is the well-known supplementary variable technique, and the other is the shift operator method in difference equations theory. The most important reason why we adopt the above approach is that we want to avoid discussing the transition probability matrix associated with the embedded Markov chain. Because with the increase in the complexity involved in the queue, the derivation of the transition probability matrix becomes extremely difficult, and many practitioners cannot fully master these complicated and tedious probabilistic arguments. In essence, it is our intention to solve a practical queueing problem in the most simple and pragmatic way using the roots of the model’s characteristic equation. From the algorithmic steps and numerical experiments presented in our work, we may also see that the methodology is nicely implemented in flexible scientific computing software that is easy to use even for users who are not professional mathematicians. A feasible plan for further study is to consider the discrete-time counterparts of this queue. Since several possible events may occur simultaneously in discrete-time queues, the analysis and computation will become more elaborate under such a situation.