On Marcinkiewicz–Zygmund Inequalities and $A_p$-Weights for $L$-Shape Arcs

Abstract

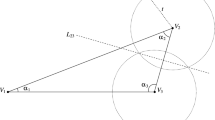
Let $\Gamma$ be an $L$-shape arc consisting of 2 line segments that meet at an angle different from $\pi$ in the complex $z$-plane ${\mathbb C}$. Application of the exterior conformal map $\psi$ from $|w| > 1$ onto ${\mathbb C}\backslash \Gamma$, with $\psi (\infty )= \infty$, introduces the level curves $\Gamma _n=\{z= \psi (w):|w|=1+{1\over {n+1}}\}$. Let $\psi ^*$ denote the continuous extension of $\psi$ from $|w|> 1$ to $|w|\ge 1$, so that any family $\{z_{n,k}: k = 0, 1, \dots , n\}$ of points on $\Gamma$ can be written as $\{z_{n,k} = \psi ^*(w_{n,k})\}$, where $|w_{n,k}|= 1$. Let $\omega _n (z)= \Pi ^n_{k=0} (z-z_{n,k})$. The main objective of this paper is to show that for $L$-shape arcs, validation of the Marcinkiewicz–Zygmund inequalities is equivalent to that of the totality of the $A_p$-weight conditions of $|\omega _n (z) |$ on $\Gamma _n$ and a mild separation condition of $\{z_{n,k}\}$. Since the Marcinkiewicz–Zygmund inequalities are essential to the study of Lagrange polynomial interpolation of continuous functions at the nodes $\{z_{n,k}\}$, another objective of this paper is to investigate the behavior of the polynomial interpolants at the Fejér points, defined by $\{z_{n,k} = \psi ^*(\mathrm{{e}}^{i(2k\pi + \theta )/(n+1)})\}$ for any choice of $\theta$. In this regard, we recall that for the interval [$-1$, 1], the Fejér points $\{z_{n,k} = \psi ^*(\mathrm{{e}}^{i(2k+1)\pi /(n+1)})\}$ agree with the Chebyshev points and that the Chebyshev points are most commonly used as nodes for Lagrange polynomial interpolation. On the other hand, numerical experimentation demonstrates that for a typical open $L$-shape arc $\Gamma$, the Lebesgue constants tend to $\infty$ at the rate of $O((\log (n))^2)$, as the polynomial degree $n$ increases, while the $A_{p}$-weight conditions for the Fejér points $\{z_{n,k}\}$ do not carry over from [$-1$, 1] to a truly $L$-shape arc. Further numerical experiments also demonstrate that the least upper bounds of the Marcinkiewicz–Zygmund inequalities for the canonical Lagrange interpolation polynomials at $\{z_{n,k}\}$ seem to grow at the rate of $n^{\beta }$, for some $\beta >0$ that depends on $p >1$.