Skip to main content
SpringerLink
Log in

Harmonic Self-Maps of \(\mathrm {SU}(3)\)

  • Published:
The Journal of Geometric Analysis Aims and scope Submit manuscript

Abstract

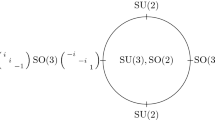
By constructing solutions of a singular boundary value problem, we prove the existence of a countably infinite family of harmonic self-maps of \(\mathrm {SU}(3)\) with non-trivial, i.e., \(\ne 0,\pm 1\), Brouwer degree.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bizon, P., Chmaj, T.: Harmonic map between spheres. Proc. R. Soc. Lond. A 453, 403–415 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  2. Eells, J., Sampson, J.: Harmonic mappings of Riemannian manifolds. Am. J. Math. 86, 109–160 (1964)

    Article  MathSciNet  MATH  Google Scholar 

  3. Eells, J., Lemaire, L.: A report on harmonic maps. Bull. Lond. Math. Soc. 10, 1–68 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  4. Eells, J., Lemaire, L.: Another report on harmonic maps. Bull. Lond. Math. Soc. 20, 385–524 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  5. Eells, J., Ratto, A.: Harmonic Maps and Minimal Immersions with Symmetries. Annals of Mathematics Studies, vol. 130. Princeton University Press, Princeton (1993)

    MATH  Google Scholar 

  6. Foscolo, L., Haskins, M.: New \(\text{G}_2\)-holonomy cones and exotic nearly Kähler structures on \(\mathbb{S}^6\) and \(\mathbb{S}^3\times \mathbb{S}^3\). arXiv:1501.07838

  7. Gastel, A.: Torus equivariant harmonic maps between spheres. Topology 41, 213–227 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  8. Gastel, A.: On the harmonic Hopf construction. Proc. Am. Math. Soc. 132, 607–615 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  9. Püttmann, T.: Cohomogeneity one manifolds and self-maps of nontrivial degree. Transform. Groups 14, 225–247 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  10. Püttmann, T., Siffert, A.: New equivariant harmonic maps between cohomogeneity one manifolds (in preparation)

  11. Siffert, A.: Infinite families of harmonic self-maps of spheres. J. Differ. Equ. 260, 2898–2925 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  12. Smith, R.T.: Harmonic mappings of spheres. Am. J. Math. 97, 364–395 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  13. Urakawa, H.: Equivariant harmonic maps between compact Riemannian manifolds of cohomogeneity one. Mich. Math. J. 40, 27–51 (1993)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

It is a pleasure to thank Wolfgang Ziller for making me aware of the Theorem of Malgrange. Furthermore, I would like to thank him for the many conservations during the last year and for the wonderful time I had at the University of Pennsylvania. The author would like to thank Deutsche Forschungsgemeinschaft for supporting this work with the grant SI 2077/1-1. Furthermore, I would also like to thank the Max Planck Institute for Mathematics for the support and the excellent working conditions.

Author information

Authors and Affiliations

  1. Max-Planck-Institut für Mathematik, Vivatsgasse 7, 53111, Bonn, Germany

    Anna Siffert

Authors
  1. Anna Siffert
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Anna Siffert.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Siffert, A. Harmonic Self-Maps of \(\mathrm {SU}(3)\) . J Geom Anal 28, 587–605 (2018). https://doi.org/10.1007/s12220-017-9833-0

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12220-017-9833-0

Keywords

Mathematics Subject Classification

Search

Navigation