Skip to main content
SpringerLink
Log in

Control of Convection Patterning and Intensity in Shallow Cavities by Harmonic Vibrations

  • ORIGINAL ARTICLE
  • Published:
Microgravity Science and Technology Aims and scope Submit manuscript

Abstract

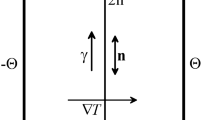
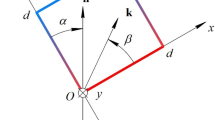
In this article the interplay among different types of flow (i.e. induced by driving forces of a different nature) is presented as a possible and “natural” means to control convection patterning and strength in shallow rectangular cavities of finite extent (A =length/height =4) filled with a low Prandtl number liquid (silicon, Pr =0.01). A variety of results concerning the possible spatial structure of the “mixed” states of steady Buoyant, Marangoni and Vibrational convection are discussed with the express intent of supporting the optimization of future experiments to be performed onboard the International Space Station.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  • Ahadi, A.H., Saghir, M.Z.: Quasi steady state effect of micro vibration from two space vehicles on mixture during thermodiffusion experiment. Fluid Dyn. Mater. Process. 8(4), 397–422 (2012)

    Google Scholar 

  • Batchelor, G. K.: Heat convection and buoyancy effects in fluids. Q. J. R. Met. Soc. 80, 339–358 (1954)

    Article  Google Scholar 

  • Ben Hadid, H., Roux, B.: Thermocapillary convection in long horizontal layers of low-Prandtl number melts subject to a horizontal temperature gradient. J. Fluid Mech. 221, 77–103 (1990)

    Article  Google Scholar 

  • Birikh, R.V., Briskman, V.A., Chernatynski, V.I., Roux, B.: Conrol of thermocapillary convection in a liquid bridge by high frequency vibrations. Microgravity Q. 3, 23–28 (1993)

    Google Scholar 

  • Bontoux, P., Roux, B., Schiroky, G. H., Markham, B. L., Rosenberger, F.: Convection in the vertical midplane of a horizontal cylinder. Comparison of two-dimensional approximations with three-dimensional results. Int. J. Heat Mass Transfer 29(2), 227–240 (1986)

    Article  Google Scholar 

  • Carotenuto, L., Piccolo, C., Castagnolo, D., Lappa, M., Garcìa-Ruiz J.M.: Experimental observations and numerical modelling of diffusion-driven crystallisation processes. Acta Crystallographica D 58, 1628–1632 (2002)

    Article  Google Scholar 

  • Castagnolo, D., Lombardi, S., Albanese, C., Ceriello, A., De Chiara, G., Di Costanzo, G., Lappa, M., Piccolo, C., Scognamiglio, M., Sorrentino, D., Tempesta, S., Beestermoeller, H.J., Cardano, M., Lippi P.: Fluid Science Laboratory on board ISS: Two years of successful operations”, 63rd International Astronautical Congress 2012 (Naples, Italy, 1-5 October 2012), paper number: IAC-12.B6.1.5x15262, 6,2012, Pages 4949-4952 (ISBN: 978-162276979-7) (2012)

  • Cormack, D. E., Leal, L. G., Imberger, J.: Natural convection in a shallow cavity with differentially heated end walls, Part 1. Asymptotic Theory. J. Fluid Mech. 65, 209–229 (1974)

    Article  MATH  Google Scholar 

  • Gelfgat, A. Yu., Bar-Yoseph, P. Z.: The effect of an external magnetic field on oscillatory instability of convective flows in a rectangular cavity. Phys. Fluids 13(8), 2269–2278 (2001)

    Article  MATH  Google Scholar 

  • Gelfgat, A.Yu: Different modes of rayleigh-benard instability in two- and three-dimensional rectangular enclosures. J. Comput. Phys. 156, 300–324 (1999)

    Article  MATH  Google Scholar 

  • Gelfgat, A.Yu., Bar-Yoseph, P.Z., Yarin, A.L.: Stability of multiple steady states of convection in laterally heated cavities. J. Fluid Mech. 388, 315–334 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  • Gershuni, G.Z., Lyubimov, D.V.: Thermal vibrational convection. Wiley (1998)

  • Haslavsky, V., Miroshnichenko, E., Kit, E., Gelfgat, A. Yu: Comparison and a possible source of disagreement between experimental and numerical results in a czochralski model. Fluid Dyn. Mater. Process. 9(3), 209–234 (2013)

    Google Scholar 

  • Hurle, D.T.J, Jakeman, E., Johnson, J.P.: Convective temperature oscillations in molten gallium. J. Fluid Mech. 64, 565–576 (1974)

    Article  Google Scholar 

  • Kozlov, V.G.: Vibrational thermal convection in a cavity executing high-frequency rocking motions. Izv. AN SSSR. Mech. Zhidk. Gasa. 3, 138–144 (1988). Translated: Fluid Dyn., 23, 437–442

    Google Scholar 

  • Kozlov, V.G., Selin, N.V.: Pendulum thermal vibrational convection in a liquid layer with internal heat generation. Fluid Dyn. Mater. Process. 2(2), 107–117 (2006)

    Google Scholar 

  • Kuhlmann, H.C., Lappa, M., Melnikov, D., Mukin, R., Muldoon, F.H., Pushkin, D., Shevtsova, V.S., Ueno, I.: The JEREMI-Project on thermocapillary convection in liquid bridges. Part A: Overview of Particle Accumulation Structures. Fluid Dyn. Mater. Process. 10(1), 1–36 (2014)

    Google Scholar 

  • Lappa, M.: Growth and Mutual Interference of Protein Seeds under reduced gravity conditions. Phys. Fluids 15(4), 1046–1057 (2003a)

    Article  MATH  Google Scholar 

  • Lappa, M.: Three-dimensional numerical simulation of Marangoni flow instabilities in floating zones laterally heated by an equatorial ring. Phys. Fluids 15(3), 776–789 (2003b)

    Article  MATH  Google Scholar 

  • Lappa, M.: Fluids, materials and microgravity: Numerical techniques and insights into the physics. Elsevier Science, Oxford (2004a)

    Google Scholar 

  • Lappa, M.: Combined effect of volume and gravity on the three-dimensional flow instability in non-cylindrical floating zones heated by an equatorial ring. Phys. Fluids 16(2), 331–343 (2004b)

    Article  MathSciNet  MATH  Google Scholar 

  • Lappa, M.: On the nature and structure of possible three-dimensional steady flows in closed and open parallelepipedic and cubical containers under different heating conditions and driving forces. Fluid Dyn. Mater. Process. 1, 1–19 (2005)

    Google Scholar 

  • Lappa, M.: Secondary and oscillatory gravitational instabilities in canonical three-dimensional models of crystal growth from the melt, Part1: Rayleigh-Bènard systems. Comptes Rendus Mécanique 335, 253–260 (2007). M. Lappa, (2007), “Secondary and oscillatory gravitational instabilities in canonical three-dimensional models of crystal growth from the melt, Part2: Lateral heating and the Hadley circulation”, Comptes Rendus Mécanique, Vol. 335, pp. 261-268.

    Article  Google Scholar 

  • Lappa, M.: Thermal convection: Patterns, evolution and stability. John Wiley, Chichester (2009)

    Book  MATH  Google Scholar 

  • Lappa, M.: Rotating thermal flows in natural and industrial processes. John Wiley, Chichester (2012a)

    Book  MATH  Google Scholar 

  • Lappa, M.: Exact solutions for thermal problems: Buoyancy, marangoni, vibrational and magnetic-field-controlled flows. Review of Applied Physics 1(1), 1–14 (2012b)

    Google Scholar 

  • Lappa, M.: On the existence and multiplicity of one-dimensional solid particle attractors in time-dependent Rayleigh-Bénard convection. Chaos 23(1), 013–105 (2013a). (9 pages)

    Article  MathSciNet  Google Scholar 

  • Lappa, M.: Assessment of the role of axial vorticity in the formation of Particle Accumulation Structures (PAS) in supercritical Marangoni and hybrid thermocapillary-rotation-driven flows. Phys. Fluids 25(1), 012–101 (2013b). (11 pages)

    Article  MathSciNet  Google Scholar 

  • Lappa, M.: On the variety of particle accumulation structures under the effect of gjitters. J. Fluid Mech. 726, 160–195 (2013c)

    Article  MathSciNet  MATH  Google Scholar 

  • Lappa, M.: Stationary solid particle attractors in standing waves. Phys. Fluids 26(1), 013–305 (2014a). (12 pages)

  • Lappa, M.: The patterning behaviour and accumulation of spherical particles in a vibrated non-isothermal liquid. Phys. Fluids 26 (2014b)

  • Lappa, M., Castagnolo, D., Carotenuto, L.: Sensitivity of the non-linear dynamics of Lysozyme ‘Liesegang Rings’ to small asymmetries. Physica A: Statistical Mechanics and its Applications 314(1-4), 623–635 (2002)

    Article  Google Scholar 

  • Lappa, M., Piccolo, C., Carotenuto, L.: Mixed buoyant-Marangoni convection due to dissolution of a droplet in a liquid-liquid system with miscibility gap. European Journal of Mechanics/B Fluids 23, 781–794 (2004)

    Article  MATH  Google Scholar 

  • Lappa, M., Yasushiro, S., Imaishi, N.: 3D numerical simulation of on ground Marangoni flow instabilities in liquid bridges of low Prandtl number fluid. Int. J. Num. Meth. Heat Fluid Flow 13(3), 309–340 (2003)

    Article  MATH  Google Scholar 

  • Luijkx, J. M., Platten, J. K.: On the onset of free convection in a rectangular channel. J. Non-Equilibrium Thermodynam. 6, 141–148 (1981)

    Article  MATH  Google Scholar 

  • Lyubimov, D. V., Popov, D. M., Lyubimova, T. P.: Stability of plane-parallel pulsational flow of two miscible fluids under high frequency horizontal vibrations. Microgravity Sci. Technol. 25(4), 231–236 (2013)

    Article  Google Scholar 

  • Lyubimova, T., Beysens, D., Gandikota, G., Amiroudine, S.: Vibration effect on a thermal front propagation in a square cavity filled with incompressible fluid. Microgravity Science and Technology 26(1), 51–56 (2014)

    Article  Google Scholar 

  • Monti, R., Savino, R.: Microgravity experiment acceleration tolerability on space orbiting laboratories. J. Spacecr. Rocket. 33(5), 707–716 (1996)

    Article  Google Scholar 

  • Oueslati, F.S., Bennacer, R., Sammouda, H., El Ganaoui, M.: Analytical and numerical solutions for natural convection in a shallow cavity filled with two immiscible fluids: Shear stress action. Numerical Heat Transfer, Part A: Applications 62(8), 605–623 (2012)

    Article  Google Scholar 

  • Parsa, A., Saghir, M.Z.: Fluid flow behavior of a binary mixture under the influence of external disturbances using different density models. Fluid Dyn. Mater. Process. 8(1), 27–50 (2012)

    MathSciNet  Google Scholar 

  • Roux, B.: Numerical Simulation of oscillatory convection in low-Pr fluids,a GAMM Workshop, Notes on numerical fluid mechanics, vol. 27. Vieweg (1990)

  • Savino, R., Monti, R.: Convection induced by residual-g and g-jitters in diffusion experiments. Int. J. Heat Mass Transfer 42(1), 111–126 (1998)

    Article  MATH  Google Scholar 

  • Sekhon, M., Armour, N., Dost, S: Numerical simulation of liquid phase diffusion growth of SiGe single crystals under zero gravity. Fluid Dyn. Mater. Process. 9(4), 331–352 (2013)

    Google Scholar 

  • Shemirani, M. M., Saghir, M. Z.: An alternative approach to minimize the convection in growing a large diameter single bulk crystal of Si0:25Ge0:75 alloy in a vertical bridgman furnace. Fluid Dyn. Mater. Process. 9(1), 11–22 (2013)

    Google Scholar 

  • Shevtsova, V., Gaponenko, Y., Kuhlmann, H.C., Lappa, M., Lukasser, M., Matsumoto, S., Mialdun, A., Montanero, J.M., Nishino, K., Ueno, I.: The JEREMI-project on thermocapillary convection in liquid bridges. Part B: Impact of co-axial gas flow. Fluid Dyn. Mater. Process. 10(2), 197–240 (2014)

    Google Scholar 

  • Shevtsova, V., Mialdun, A., Kawamura, H., Ueno, I., Nishino, K., Lappa, M.: Onset of hydrothermal instability in liquid bridge. Experimental benchmark. Fluid Dyn. Mater. Process. 7(1), 1–28 (2011a)

    Google Scholar 

  • Shevtsova, V., Mialdun, A., Melnikov, D., Ryzhkov, I., Gaponenko, Y., Saghir, Z., Lyubimova, T., Legros, J. C.: The IVIDIL experiment onboard the ISS: Thermodiffusion in the presence of controlled vibrations. Compt. Rend. Mécaniq. 339(5), 310–317 (2011b)

    Article  Google Scholar 

  • Shevtsova, V., Lyubimova, T., Saghir, Z., Melnikov, D., Gaponenko, Y., Sechenyh, V., Legros, J. C., Mialdun, A.: IVIDIL: On-board g-jitters and diffusion controlled phenomena. J. Phys.: Conf. Ser 327 (012031) (2011c)

  • Simanovskii, I. B., Kabov, O. A.: Nonlinear Convective Oscillations in Two-Layer Systems with Different Aspect Ratios. Microgravity Science and Technology 24(2), 127–137 (2012)

    Article  Google Scholar 

  • Skeldon, A. C., Riley, D. C., Cliffe, K. A.: Convection in a low Prandtl number fluid. J. Cryst. Growth 162, 95–106 (1996)

    Article  Google Scholar 

  • Trinchero, G., Cardano, M., Pensavalle, E., Bassano, E., Dell’Aversana, P., Lappa, M., Tacconi, M.: The Fluid Science Laboratory on the ISS Columbus module Performances and Operations”, 3rd International Symposium on Physical Sciences in Space ISPS:2007, Nara, Japan, 22-26 (2007)

  • Winters, K. H.: Oscillatory convection in liquid metals in a horizontal temperature gradient. Int. J. Num. Meth. Eng. 25, 401–414 (1988)

    Article  MATH  Google Scholar 

  • Zhou, X., Huai, X.: Numerical investigation of thermocapillary convection in a liquid layer with free surface. Microgravity Science and Technology 25(6), 335–341 (2014)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical and Aerospace Engineering, University of Strathclyde, James Weir Building, 75 Montrose Street, Glasgow, G1 1XJ, UK

    Marcello Lappa

Authors
  1. Marcello Lappa
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marcello Lappa.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lappa, M. Control of Convection Patterning and Intensity in Shallow Cavities by Harmonic Vibrations. Microgravity Sci. Technol. 28, 29–39 (2016). https://doi.org/10.1007/s12217-015-9467-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12217-015-9467-4

Keywords

Search

Navigation