Skip to main content
SpringerLink
Log in

Fuzzy Fractional-Order Fast Terminal Sliding Mode Control for Some Chaotic Microcomponents

  • Research article
  • Published:
Transactions of Tianjin University Aims and scope Submit manuscript

Abstract

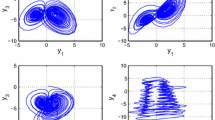
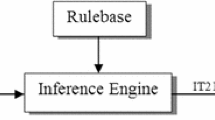
In this paper, we propose a novel fractional-order fast terminal sliding mode control method, based on an integer-order scheme, to stabilize the chaotic motion of two typical microcomponents. We apply the fractional Lyapunov stability theorem to analytically guarantee the asymptotic stability of a system characterized by uncertainties and external disturbances. To reduce chattering, we design a fuzzy logic algorithm to replace the traditional signum function in the switching law. Lastly, we perform numerical simulations with both the fractional-order and integer-order control laws. Results show that the proposed control law is effective in suppressing chaos.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Andrievskii BR, Fradkov AL (2003) Control of chaos: methods and applications. I. Methods. Autom Remote Control 64(5):673–713

    Article  MathSciNet  MATH  Google Scholar 

  2. Drăgănescu GE, Bereteu L, Ercuţa A et al (2010) Anharmonic vibrations of a nano-sized oscillator with fractional damping. Commun Nonlinear Sci Numer Simul 15(4):922–926

    Article  MathSciNet  MATH  Google Scholar 

  3. Tavazoei MS, Haeri M (2008) Chaos control via a simple fractional-order controller. Phys Lett A 372(6):798–807

    Article  MATH  Google Scholar 

  4. Efe MÖ (2012) A sufficient condition for checking the attractiveness of a sliding manifold in fractional order sliding mode control. Asian J Control 14(4):1118–1122

    Article  MathSciNet  MATH  Google Scholar 

  5. Tang YG, Zhang XY, Zhang DL et al (2013) Fractional order sliding mode controller design for antilock braking systems. Neurocomputing 111:122–130

    Article  Google Scholar 

  6. Dadras S, Momeni HR (2012) Fractional terminal sliding mode control design for a class of dynamical systems with uncertainty. Commun Nonlinear Sci Numer Simul 17(1):367–377

    Article  MathSciNet  MATH  Google Scholar 

  7. Yin C, Zhong SM, Chen WF (2012) Design of sliding mode controller for a class of fractional-order chaotic systems. Commun Nonlinear Sci Numer Simul 17(1):356–366

    Article  MathSciNet  MATH  Google Scholar 

  8. Delavari H, Ghaderi R, Ranjbar A et al (2010) Fuzzy fractional order sliding mode controller for nonlinear systems. Commun Nonlinear Sci Numer Simul 15(4):963–978

    Article  MathSciNet  MATH  Google Scholar 

  9. Podlubny I (1998) Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Academic Press, New York

    MATH  Google Scholar 

  10. Li CP, Deng WH (2007) Remarks on fractional derivatives. Appl Math Comput 187(2):777–784

    MathSciNet  MATH  Google Scholar 

  11. Li Y, Chen YQ, Podlubny I (2010) Stability of fractional-order nonlinear dynamic systems: lyapunov direct method and generalized Mittag-Leffler stability. Comput Math Appl 59(5):1810–1821

    Article  MathSciNet  MATH  Google Scholar 

  12. Yu SH, Yu XH, Shirinzadeh B et al (2005) Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 41(11):1957–1964

    Article  MathSciNet  MATH  Google Scholar 

  13. Aghababa MP (2013) A switching fractional calculus-based controller for normal non-linear dynamical systems. Nonlinear Dyn 75(3):577–588

    Article  MathSciNet  MATH  Google Scholar 

  14. Yau HT, Wang CC, Hsieh CT et al (2011) Nonlinear analysis and control of the uncertain micro-electro-mechanical system by using a fuzzy sliding mode control design. Comput Math Appl 61(8):1912–1916

    Article  MathSciNet  MATH  Google Scholar 

  15. Oustaloup A, Levron F, Mathieu B et al (2000) Frequency-band complex noninteger differentiator: characterization and synthesis. IEEE Trans Circ Syst I Fund Theory Appl 47(1):25–39

    Article  Google Scholar 

  16. Haghighi HS, Markazi AHD (2010) Chaos prediction and control in MEMS resonators. Commun Nonlinear Sci Numer Simul 15(10):3091–3099

    Article  Google Scholar 

  17. Bahrami A, Nayfeh AH (2012) On the dynamics of tapping mode atomic force microscope probes. Nonlinear Dyn 70(2):1605–1617

    Article  Google Scholar 

  18. Basso M, Giarre L, Dahleh M et al (2000) Complex dynamics in a harmonically excited Lennard-Jones oscillator: microcantilever-sample interaction in scanning probe microscopes. J Dyn Syst Meas Control Trans ASME 122(1):240–245

    Article  Google Scholar 

Download references

Acknowledgements

This study was supported by the National Natural Science Foundation of China (No. 11372210 and No. 51405343), the Research Fund for the Doctoral Program of Higher Education of China (No. 20120032110010) and Tianjin Research Program of Application Foundation and Advanced Technology (No. 12JCZDJC28000 and No. 15JCQNJC05000).

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Tianjin University, Tianjin, 300350, China

    Jianxin Han, Qichang Zhang, Wei Wang & Jing Wang

  2. Tianjin Key Laboratory of High Speed Cutting and Precision Machining, Tianjin University of Technology and Education, Tianjin, 300222, China

    Jianxin Han

  3. Tianjin Key Laboratory of Nonlinear Dynamics and Control, Tianjin, 300350, China

    Jianxin Han, Qichang Zhang, Wei Wang & Jing Wang

Authors
  1. Jianxin Han
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qichang Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wei Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jing Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wei Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Han, J., Zhang, Q., Wang, W. et al. Fuzzy Fractional-Order Fast Terminal Sliding Mode Control for Some Chaotic Microcomponents. Trans. Tianjin Univ. 23, 289–294 (2017). https://doi.org/10.1007/s12209-017-0050-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12209-017-0050-5

Keywords

Search

Navigation