Skip to main content
SpringerLink
Log in

Measurement of moment of inertia based on hilbert transform

  • Published:
Transactions of Tianjin University Aims and scope Submit manuscript

Abstract

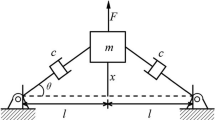
A measurement model based on torsion pendulum was established, in which nonlinear damping and nonlinear restoring force were considered. The calculation method of the moment of inertia was based on Hilbert transform. The motion of torsion pendulum showed the time-frequency characteristics due to the nonlinear factors, which were validated by the experimental data. The analytical signal was formed by Hilbert transform of the angular displacement signal of the test object. The moment of inertia can be computed by the instantaneous undamped natural frequency with Hilbert transform. Prior to the implementation of Hilbert transform, the empirical mode decomposition was used to filter the experimental signal. The moment of inertia of the test object was measured by the torsion pendulum system. The experimental results show that the relative measurement error of the moment of inertia was within 0.7%, which indicated the validity of the measurement method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Carsten Schedlinski, Michael Link. A survey of current inertia parameter identification methods[J]. Mechanical Systems and Signal Processing, 2001, 15(1): 189–211.

    Article  Google Scholar 

  2. Yuan Changsheng, Song Bifeng. Theory and equipment to determine the moments of inertia by an improved compound-pendulum method[J]. China Mechanical Engineering, 2006, 17(6): 598–600 (in Chinese).

    Google Scholar 

  3. de Jong R C, Mulder J A. Accurate estimation of aircraft inertia characteristics from a single suspension experiment[ J]. Journal of Aircraft, 1987, 24(6): 362–370.

    Article  Google Scholar 

  4. Ringegni P L, Actis M D, Patanella A J. An experimental technique for determining mass inertial properties of irregular shape bodies and mechanical assemblies[J]. Measurement, 2001, 29(1): 63–75.

    Article  Google Scholar 

  5. Hou Zhichao, Lu Yining, Lao Yaoxin et al. A new trifilar pendulum approach to identify all inertia parameters of a rigid body or assembly[J]. Mechanism and Machine Theory, 2009, 44(6): 1270–1280.

    Article  MATH  Google Scholar 

  6. Harris C M, Piersol A G, Paez T L. Harris’ Shock and Vibration Handbook[M]. McGraw-Hill, New York, 2009.

    Google Scholar 

  7. Li Huayi, Zhang Yingchun, Li Baohua et al. Analysis and design of the moment of inertia(MOI) measuring instrument with high accuracy[J]. Acta Metrologica Sinica, 2004, 25(3): 250–253 (in Chinese).

    Google Scholar 

  8. Matt R Jardin, Eric R Mueller. Optimized measurements of unmanned-air-vehicle mass moment of inertia with a bifilar pendulum[J]. Journal of Aircraft, 2009, 46(3): 763–775.

    Article  Google Scholar 

  9. Tjahjowidodo T, Al-Bender F, Van Brussel H. Nonlinear modelling and identification of torsional behaviour in harmonic drives[C]. In: International Conference on Noise and Vibration Engineering. Leuven, Belgium, 2006.

    Google Scholar 

  10. Feldman M. Nonlinear free vibration identification via the Hilbert transform [J]. Journal of Sound and Vibration, 1997, 208(3): 475–489.

    Article  MathSciNet  MATH  Google Scholar 

  11. Zhao Yan, Zhang Xiaolin, Wang Jun et al. Measurement of the moment of inertia under nonlinear damping condition[ J]. Journal of Vibration and Shock, 2012, 31(21): 37–40 (in Chinese).

    Google Scholar 

  12. Huang N E, Wu M C, Long S R et al. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis[J]. Proceedings of Royal Society of London, Series A, 2003, 459(2037): 2317–2345.

    Article  MathSciNet  MATH  Google Scholar 

  13. Huang N E, Shen Z, Long S R et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of Royal Society of London, Series A, 1998, 454(1971): 903–995.

    Article  MathSciNet  MATH  Google Scholar 

  14. Wang Lili, Zhang Jinghui, Wang Chao et al. Timefrequency analysis of nonlinear systems: The skeleton linear model and the skeleton curves[J]. Journal of Vibration and Acoustics, 2003, 125(2): 170–177.

    Article  Google Scholar 

  15. Li Huipeng, Tang Wenyan, Zhang Chunfu et al. A measuring system of inertia moment of missile and its error analysis[ J]. Acta Armamentarii, 2007, 28(2): 206–208 (in Chinese).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Electrical Engineering and Automation, Harbin Institute of Technology, Harbin, 150001, China

    Yan Zhao  (赵 岩), Xiaolin Zhang  (张晓琳), Jun Wang  (王 军) & Wenyan Tang  (唐文彦)

Authors
  1. Yan Zhao  (赵 岩)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaolin Zhang  (张晓琳)
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jun Wang  (王 军)
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Wenyan Tang  (唐文彦)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wenyan Tang  (唐文彦).

Additional information

Zhao Yan, born in 1984, male, doctorate student.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhao, Y., Zhang, X., Wang, J. et al. Measurement of moment of inertia based on hilbert transform. Trans. Tianjin Univ. 19, 225–230 (2013). https://doi.org/10.1007/s12209-013-1903-1

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12209-013-1903-1

Keywords

Search

Navigation