Skip to main content
SpringerLink
Log in

Rate-dependent hysteresis modeling and compensation of piezo-driven flexure-based mechanism

  • Published:
Transactions of Tianjin University Aims and scope Submit manuscript

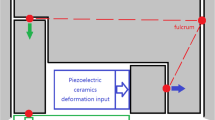
Abstract

Updating parameters according to the driving rate of input, the rate-dependent Prandtl-Ishlinskii (PI) model is widely used in hysteresis modeling and compensation. In order to improve the modeling accuracy, two PI models identified at low and high driving rates separately are incorporated through a combination law. For the piezo-driven flexure-based mechanism, the very low damping ratio makes it easy to excite the structural vibration. As a result, the measured hysteresis loop is greatly distorted and the modeling accuracy of the identified PI model is significantly affected. In this paper, a novel time-efficient parameter identification method which utilizes the superimposed sinusoidal signals as the control input is proposed. This method effectively avoids the excitation of the structural vibration. In addition, as the driving rate of the superimposed sinusoidal signals covers a wide range, all the coefficients required for modeling the rate-dependence can be identified through only one set of experimental data. Hysteresis modeling and trajectory tracking experiments were performed on a 2-DOF piezo-driven flexure-based mechanism. The experimental results show that the combined hysteresis model maintains the modeling accuracy over the entire working range of the flexure-based mechanism. The mechanism’s hysteresis is significantly suppressed by the use of the inverse PI model as the feedforward controller; and better result is achieved when a feedback loop is also incorporated. The tracking performance of the flexure-based mechanism is greatly improved.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Fleming A J, Moheimani S O R. Sensorless vibration suppression and scan compensation for piezoelectric tube nanopositioners [J]. IEEE Transactions on Control Systems Technology, 2006, 14(1): 33–44.

    Article  Google Scholar 

  2. Clayton G M, Tien S, Fleming A J et al. Inversefeedforward of charge-controller piezopositioners [J]. Mechatronics, 2008, 18(5/6): 273–281.

    Article  Google Scholar 

  3. Yong Y K, Liu K, Moheimani S O R. Reducing crosscoupling in a compliant XY nanopositioner for fast and accurate raster scanning[J]. IEEE Transactions on Control Systems Technology, 2010, 18(5): 1172–1179.

    Article  Google Scholar 

  4. Ge P, Jouaneh M. Tracking control of a piezoceramic actuator[ J]. IEEE Transactions on Control Systems Technology, 1996, 4(3): 209–216.

    Article  Google Scholar 

  5. Mayergoyz I D. Mathematical models of hysteresis[J]. IEEE Transactions on Magnetics, 1986, 22(5): 603–608.

    Article  Google Scholar 

  6. Ge P, Jouaneh M. Modeling hysteresis in piezoceramic actuators[J]. Precision Engineering, 1995, 17(3): 211–221.

    Article  Google Scholar 

  7. Ge P, Jouaneh M. Generalized preisach model for hysteresis nonlinearity of piezoceramic actuators[J]. Precision Engineering, 1997, 20(2): 99–111.

    Article  Google Scholar 

  8. Leang K K, Devasia S. Iterative feedforward compensation of hysteresis in piezo positioners[C]. In: Proceedings of the 42nd IEEE Conference on Decision and Control. Maui, Hawaii, USA, 2003. 2626–2631.

  9. Leang K K, Devasia S. Design of hysteresis-compensating iterative learning control for piezo-positioners: Application to atomic force microscopes[J]. Mechatronics, 2006, 16(3/4): 141–158.

    Article  Google Scholar 

  10. Bashash S, Jalili N. Robust multiple frequency trajectory tracking control of piezoelectrically driven micro/nanopositioning systems[J]. IEEE Transactions on Control Systems Technology, 2007, 15(5): 867–878.

    Article  Google Scholar 

  11. Ang W T, Khosla P K, Riviere C N. Feedforward controller with inverse rate-dependent model for piezoelectric actuators in trajectory-tracking applications[J]. IEEE/ASME Transactions on Mechatronics, 2007, 12(2): 134–142.

    Article  Google Scholar 

  12. Park J, Moon W. Hysteresis compensation of piezoelectric actuators: The modified Rayleigh model[J]. Ultrasonics, 2010, 50(3): 335–339.

    Article  Google Scholar 

  13. Choi G S, Lim Y A, Choi G H. Tracking position control of piezoelectric actuators for periodic reference inputs[J]. Mechatronics, 2002, 12(5): 669–684.

    Article  MathSciNet  Google Scholar 

  14. Liu Y T, Chang K M, Li W Z. Model reference adaptive control for a piezo-positioning system[J]. Precision Engineering, 2010, 34(1): 62–69.

    Article  Google Scholar 

  15. Ru C, Chen L, Shao B et al. A hysteresis compensation method of piezoelectric actoator: Model, identification and control[J]. Control Engineering Practice, 2009, 17(9): 1107–1114.

    Article  Google Scholar 

  16. Song G, Zhao J, Zhou X et al. Tracking control of a piezoceramic actuator with hysteresis compensation using inverse Preisach model[J]. IEEE/ASME Transactions on Mechatronics, 2005, 10(2): 198–209.

    Article  Google Scholar 

  17. Cruz-Hernandez J M. Phase control approach to hysteresis reduction[J]. IEEE Transactions on Control Systems Technology, 2001, 9(1): 17–26.

    Article  Google Scholar 

  18. Fleming A J, Leang K K. Integrated strain and force feedback for high-performance control of piezoelectric actuators[ J]. Sensors and Actuators A: Physical, 2010, 161(1/2): 256–265.

    Article  Google Scholar 

  19. Liaw H C, Shirinzadeh B, Smith J. Enhanced sliding mode motion tracking control of piezoelectric actuators[J]. Sensors and Actuators A: Physical, 2007, 138(1): 194–202.

    Article  Google Scholar 

  20. Zhong J, Yao B. Adaptive robust precision motion control of a piezoelectric positioning stage[J]. IEEE Transactions on Control Systems Technology, 2008, 16(5):1039–1046.

    Article  Google Scholar 

  21. Zhou J, Wen C, Zhang Y. Adaptive backstepping control of a class of uncertain nonlinear systems with unknown backlash-like hysteresis[J]. IEEE Transactions on Automatic Control, 2004, 49(10): 1751–1757.

    Article  MathSciNet  Google Scholar 

  22. Wang Q, Su C Y. Robust adaptive control of a class of nonlinear systems including actuator hysteresis with Prandtl-Ishlinskii presentations[J]. Automatica, 2006, 42(5): 859–867.

    Article  MathSciNet  MATH  Google Scholar 

  23. Kuhnen K, Janocha H. Inverse feedforward controller for complex hysteretic nonlinearities in smart-material systems[ J]. Control and Intelligent Systems, 2001, 29(3): 74–83.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Tianjin University, Tianjin, 300072, China

    Yanding Qin  (秦岩丁), Weiguo Gao  (高卫国) & Dawei Zhang  (张大卫)

Authors
  1. Yanding Qin  (秦岩丁)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Weiguo Gao  (高卫国)
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dawei Zhang  (张大卫)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Weiguo Gao  (高卫国).

Additional information

Supported by National Natural Science Foundation of China (No. 51175372) and National Key Special Project of Science and Technology of China (No. 2011ZX04016-011).

QIN Yanding, born in 1983, male, doctorate student.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Qin, Y., Gao, W. & Zhang, D. Rate-dependent hysteresis modeling and compensation of piezo-driven flexure-based mechanism. Trans. Tianjin Univ. 18, 157–167 (2012). https://doi.org/10.1007/s12209-012-1846-y

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12209-012-1846-y

Keywords

Search

Navigation