Skip to main content
SpringerLink
Log in

Scheduling of household power consumption for Step and Time-of-Use tariff system

  • Published:
Transactions of Tianjin University Aims and scope Submit manuscript

Abstract

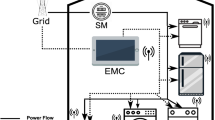
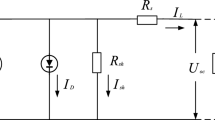
This paper proposes a hybrid optimization to solve the scheduling of household power consumption for Step and Time-of-Use (TOU) tariff system. The target function is the cost of electricity, and the optimization object is total instantaneous power within a billing period. The control variables are starting moments of each household appliance. The optimization procedure is divided into two stages. Firstly, the prerequisite for minimal cost is calculated through mathematical analysis and generalized function theory. Secondly, the solution is obtained by using a heuristic algorithm in which the result of the first stage is considered to reduce the searching space. And an evaluation methodology is deduced to evaluate the optimization. The computer simulation demonstrates that the proposed approach can reduce the cost of electricity evidently in the sense of probability. The approach shows great value for embedded applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Yu Yixin, Luan Wenpeng. Smart grid[J]. Power System and Clean Energy, 2009, 25(1): 7–11 (in Chinese).

    Google Scholar 

  2. Farhangi H. The path of the smart grid[J]. Power and Energy Magazine, IEEE, 2010, 8(1): 18–28.

    Article  MathSciNet  Google Scholar 

  3. Hart D G. Using AMI to realize the smart grid[C]. In: Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century. Pittsburgh, 2008. 1–2.

  4. Potter C W, Archambault A, Westrick K. Building a smarter smart grid through better renewable energy information[ C]. In: Power Systems Conference and Exposition. Seattle, 2009. 1–5.

  5. Roncero J R. Integration is key to smart grid management[C]. In: CIRED Seminar. Frankfurt, 2008. 1–4.

  6. Sheble G B. Smart grid millionaire[J]. Power and Energy Magazine, IEEE, 2008, 6(1): 22–28.

    Article  MathSciNet  Google Scholar 

  7. Fan Z, Kalogridis G, Efthymiou C et al. The new frontier of communications research: Smart grid and smart metering[C]. In: Procedings of the 1st International Conference on Energy-Efficient Computing and Networking. New York, 2010. 115–118.

  8. Wolsey L A, Nemhauser G L. Integer and Combinatorial Optimization[M]. Wiley, New York, 1988.

    Google Scholar 

  9. Luus R. Optimization of system reliability by a new nonlinear integer programming procedure[J]. IEEE Transactions on Reliability, 1975, 24(1): 14–16.

    Article  Google Scholar 

  10. Ingolfsson A, Campello F, Wu X D et al. Combining integer programming and the randomization method to schedule employees[J]. European Journal of Operational Research, 2010, 202(1): 153–163.

    Article  MATH  Google Scholar 

  11. Tillman F A. Optimization by integer programming of constrained reliability problems with several modes of failure[ J]. IEEE Transactions on Reliability, 2009, 18(2): 47–53.

    Article  Google Scholar 

  12. Nash S G, Sofer A. Linear and Nonlinear Programming[ M]. McGraw-Hill, New York, 1995.

    Google Scholar 

  13. Sistu P B, Bequette B W. Process identification using nonlinear programming techniques[C]. In: American Control Conference. San Diego, 1990. 1534–1539.

  14. Moreton H P, Séquin C H. Functional optimization for fair surface design[C]. In: Proceedings of the 19th Annual Conference on Computer Graphics and Interactive Techniques. New York, 1992. 167–176.

  15. Giulini S, Sanguineti M. Approximation schemes for functional optimization problems[J]. Journal of Optimization Theory and Applications, 2008, 140(1): 33–54.

    Article  MathSciNet  Google Scholar 

  16. Atkinson K, Han W M. Theoretical Numerical Analysis: A Functional Analysis Framework[M]. Springer Verlag, New York, 2010.

    Google Scholar 

  17. Bandle C, Wagner A. Optimization problems for an energy functional with mass constraint revisited[J]. Journal of Mathematical Analysis and Applications, 2008, 352(1): 400–417.

    Article  MathSciNet  Google Scholar 

  18. Guan Xiaohong, Zhai Qiaozhu, Feng Yonghan et al. Optimization based scheduling for a class of production systems with integral constraints[J]. Sci China Ser E-Tech Sci, 2010, 40(1): 41–51 (in Chinese).

    Google Scholar 

  19. Konjik S, Kunzinger M, Oberguggenberger M. Foundations of the calculus of variations in generalized function algebras[J]. Acta Applicandae Mathematicae, 2008, 103(2): 169–199.

    Article  MathSciNet  MATH  Google Scholar 

  20. Oberguggenberger M, Pilipović S, Scarpalézos D. Positivity and positive definiteness in generalized function algebras[ J]. Journal of Mathematical Analysis and Applications, 2007, 328(2): 1321–1335.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Computer Science and Technology, Tianjin University, Tianjin, 300072, China

    Jingtao Guo  (郭景涛)

  2. Tianjin Institute of Metrological Supervision and Testing, Tianjin, 300192, China

    Jingtao Guo  (郭景涛)

  3. School of Electronic Information Engineering, Tianjin University, Tianjin, 300072, China

    Zhigang Jin  (金志刚)

  4. School of Electrical Engineering and Automation, Tianjin University, Tianjin, 300072, China

    Huaidong Liu  (刘怀东)

Authors
  1. Jingtao Guo  (郭景涛)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhigang Jin  (金志刚)
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Huaidong Liu  (刘怀东)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jingtao Guo  (郭景涛).

Additional information

GUO Jingtao, born in 1979, male, doctorate student.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Guo, J., Jin, Z. & Liu, H. Scheduling of household power consumption for Step and Time-of-Use tariff system. Trans. Tianjin Univ. 17, 369–375 (2011). https://doi.org/10.1007/s12209-011-1613-5

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12209-011-1613-5

Keywords

Search

Navigation