Skip to main content
SpringerLink
Log in

Parallel volume integral equation method for three-dimensional multiple inclusion problems

  • Original Article
  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

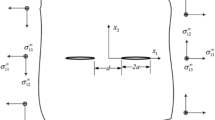
In this paper, the volume integral equation method (VIEM) is introduced for the analysis of multiple isotropic/anisotropic inclusions (or inhomogeneities) in an unbounded isotropic matrix. In order to introduce the VIEM as an accurate and efficient numerical method for the three-dimensional elastostatic inclusion (or inhomogeneity) problem, multiple isotropic/orthotropic spherical inclusions (or inhomogeneities) in an unbounded isotropic matrix under uniform remote tensile loading are investigated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J. D. Eshelby, The determination of the elastic field of an ellipsoidal inclusion, and related problems, Proceedings of the Royal Society A, 241 (1957) 376–396.

    MathSciNet  MATH  Google Scholar 

  2. J. D. Eshelby, The force on an elastic singularity, Philosophical Transactions of the Royal Society A, 244 (1951) 87–112.

    MathSciNet  MATH  Google Scholar 

  3. J. K. Lee and A. K. Mal, A volume integral equation technique for multiple scattering problems in elastodynamics, Applied Mathematics and Computation, 67 (1995) 135–159.

    Article  MathSciNet  MATH  Google Scholar 

  4. J. K. Lee and A. K. Mal, A volume integral equation technique for multiple inclusion and crack interaction problems, Journal of Applied Mechanics-Transactions of The ASME, 64 (1997) 23–31.

    Article  MATH  Google Scholar 

  5. J. Lee and H. Kim, Volume integral equation n method for multiple circular and elliptical inclusion problems in antiplane elastostatics, Composites Part B: Engineering, 43 (2012) 1224–1243.

    Article  Google Scholar 

  6. J. K. Lee, S. M. Oh and A. Mal, Calculation of interfacial stresses in composites containing elliptical inclusions of various types, European Journal of Mechanics, A/Solids, 44 (2014) 17–40.

    Article  Google Scholar 

  7. J. K. Lee and M. G. Han, Volume integral equation method solution for spheroidal inclusion problem, Materials (MDPI), 14 (2021) Article ID 6996.

  8. A. K. Mal and L. Knopoff, Elastic wave velocities in two component systems, Journal of the Institute of Mathematics and its Applications, 3 (1967) 376–387.

    Article  MATH  Google Scholar 

  9. J. K. Lee and M. G. Han, Three-dimensional volume integral equation method for solving isotropic/anisotropic inhomogeneity problems, Mathematics (MDPI), 8 (2020) Article ID 1866.

  10. J. Ma and Z. Nie, FEM-DDM with an efficient second-order transmission condition in both high-frequency and low-frequency applications, Progress in Electromagnetics Research B, 50 (2013) 253–271.

    Article  Google Scholar 

  11. P. K. Banerjee, The Boundary Element Methods in Engineering, McGraw-Hill (1993).

  12. Y.-H. Pao and V. Varatharajulu, Huygens’ principle, radiation conditions, and integral formulas for the scattering of elastic waves, The Journal of the Acoustical Society of America, 59 (1976) 1361–1369.

    Article  MATH  Google Scholar 

  13. H. B. Li, G. M. Han and H. A. Mang, A new method for evaluating singular integrals in stress analysis of solids by the direct boundary element method, International Journal for Numerical Methods in Engineering, 21 (1985) 2071–2098.

    Article  MathSciNet  MATH  Google Scholar 

  14. J. Lee, Volume integral equation method (VIEM), Advances in Computers and Information in Engineering Research, J. G. Michopoulos, D. W. Rosen, C. J. Paredis and J. M. Vance (Eds.), ASME Press, New York, USA, 2 (2021) 79–138.

    Google Scholar 

  15. MSC.Software Corporation, PATRAN 2008 r2 Release Guide, Santa Ana, CA (2008).

  16. H. R. Sadraie, S. L. Crouch and S. G. Mogilevskaya, A boundary spectral method for elastostatic problems with multiple spherical cavities and inclusions, Engineering Analysis with Boundary Elements, 31 (2007) 425–442.

    Article  MATH  Google Scholar 

  17. H. Ma, Solutions of eshelby-type inclusion problems and a related homogenization method based on a simplified strain gradient elasticity theory, Ph.D. Thesis, Texas A&M University (2010).

  18. C. Meng, W. Heltsley and D. D. Pollard, Evaluation of the Eshelby solution for the ellipsoidal inclusion and heterogeneity, Computers and Geosciences, 40 (2012) 40–48.

    Article  Google Scholar 

  19. Y.-G. Lee, W.-N. Zou and E. Pan, Eshelby’s problem of polygonal inclusions with polynomial eigenstrains in an anisotropic magneto-electro-elastic full plane, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 471 (2015) 20140827.

    Article  MathSciNet  MATH  Google Scholar 

  20. W.-N. Zou and Q.-C. He, Eshelby’s problem of a spherical inclusion eccentrically embedded in a finite spherical body, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 473 (2017) 20160808.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT, Republic of Korea (Grant No. 2015-R1A2A2A01004531) and the 2021 Hongik University Research Fund. The authors would also like to acknowledge the support of the National Supercomputing Center with supercomputing resources including technical support (No. KSC-2021-CRE-0456).

Author information

Authors and Affiliations

  1. Department of Mechanical and Design Engineering, Hongik University, Sejong City, 30016, Korea

    Jungki Lee

  2. Korea Institute of Science and Technology Information, Daejeon City, 34141, Korea

    Oh-Kyoung Kwon

Authors
  1. Jungki Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Oh-Kyoung Kwon
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jungki Lee.

Additional information

Jungki Lee is a Professor at Hongik University (Sejong Campus). He received a Ph.D. in Mechanical Engineering from the University of California, Los Angeles, USA. His research interests are computational mechanics of solids, nondestructive evaluation, and composite materials. He has been developing the volume integral equation method (VIEM) with Professor Mal at UCLA.

Oh-Kyoung Kwon is a Principle Researcher at Korea Institute Science and Technology and Information. He received a Ph.D. in Computer Science and Engineering from KAIST, Daejeon, Korea. His current research interests are optimization and paralleization of HPC applications on a large-scale system. In particular, he has experiences in parallization of scientific applications including simulation of turbulent flows, weather forecasting and cosmological hydrodynamics on top of KISTI supercomputers.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lee, J., Kwon, OK. Parallel volume integral equation method for three-dimensional multiple inclusion problems. J Mech Sci Technol 37, 239–259 (2023). https://doi.org/10.1007/s12206-022-1225-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-022-1225-0

Keywords

Search

Navigation