Skip to main content
SpringerLink
Log in

Weak fault feature extraction of rolling bearing under strong poisson noise and variable speed conditions

  • Original Article
  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

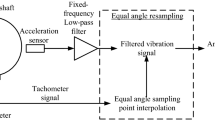
Abstract

Fault feature extraction of the rolling bearing under strong background noise is always a difficult problem in bearing fault diagnosis. At present, most of the research focuses on weak signal extraction under Gaussian white noise and has certain practical significance. However, the noise in engineering is often complex and changeable, Gaussian white noise cannot fully simulate the actual strong background noise. Poisson white noise is a type of typical non-Gaussian noise, which widely exists in complex mechanical impact. It is of great significance to study the weak fault feature extraction of a faulty bearing under this type of noise. At the same time, variable speed conditions occupy most rotating machinery speed conditions. Non-stationary vibration signals make it difficult to extract fault features, and the frequency spectrum ambiguity will occur because of speed fluctuation. To solve the above problems, a method of weak feature extraction of a faulty bearing based on computed order analysis (COA) and adaptive stochastic resonance (SR) is proposed. Firstly, by numerical simulation, the non-stationary fault characteristic signal corrupted with strong Poisson noise is transformed into a stationary signal in the angle domain by COA. Secondly, the influence of the parameters of the pulse arrival rate and noise intensity of Poisson white noise on the optimal SR response in the angle domain are studied, and the influence of the parameters of Poisson white noise on the fault feature extraction is given. Then, adaptive SR method is used to extract and enhance fault feature information. Finally, the effectiveness of this method in weak fault characteristic signal extraction under strong Poisson noise is verified by experiments. Numerical simulation and experimental results verify the effectiveness of the proposed method in bearing fault diagnosis under strong Poisson noise and variable speed conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Z. Liu and L. Zhang, A review of failure modes, condition monitoring and fault diagnosis methods for large-scale wind turbine bearings, Measurement, 149 (2020) 107002.

    Article  Google Scholar 

  2. B. Li, M. Y. Chow, Y. Tipsuwan and J. C. Hung, Neural-network-based motor rolling bearing fault diagnosis, IEEE Trans. Ind. Electron., 47(5) (2000) 1060–1069.

    Article  Google Scholar 

  3. X. Lou and K. A. Loparo, Bearing fault diagnosis based on wavelet transform and fuzzy inference, Mech. Syst. Signal Process., 18(5) (2004) 1077–1095.

    Article  Google Scholar 

  4. Y. Li, G. Cheng and C. Liu, Research on bearing fault diagnosis based on spectrum characteristics under strong noise interference, Measurement, 169 (2021) 108509.

    Article  Google Scholar 

  5. J. Yang, C. Wu, Z. Shan, H. Liu and C. Yang, Extraction and enhancement of unknown bearing fault feature in the strong noise under variable speed conditions, Meas. Sci. Technol., 32(10) (2021) 105021.

    Article  Google Scholar 

  6. Q. Jiang, F. Chang and B. Sheng, Bearing fault classification based on convolutional neural network in noise environment, IEEE Access, 7 (2019) 69795–69807.

    Article  Google Scholar 

  7. M. Grigoriu, Response of dynamic systems to Poisson white noise, J. Sound Vib., 195(3) (1996) 375–389.

    Article  MathSciNet  MATH  Google Scholar 

  8. M. Grigoriu, Dynamic systems with Poisson white noise, Nonlinear Dyn., 36(2) (2004) 255–266.

    Article  MathSciNet  MATH  Google Scholar 

  9. C. Klüppelberg and C. Kühn, Fractional Brownian motion as a weak limit of Poisson shot noise processes-with applications to finance, Stoch. Process. Their Appl., 113(2) (2004) 333–351.

    Article  MathSciNet  MATH  Google Scholar 

  10. M. Makitalo and A. Foi, Optimal inversion of the Anscombe transformation in low-count Poisson image denoising, IEEE Trans. Image Process., 20(1) (2010) 99–109.

    Article  MathSciNet  MATH  Google Scholar 

  11. W. Kumwilaisak, T. Piriyatharawet, P. Lasang and N. That-phithakkul, Image denoising with deep convolutional neural and multi-directional long short-term memory networks under Poisson noise environments, IEEE Access, 8 (2020) 86998–87010.

    Article  Google Scholar 

  12. K. Bodduna and J. Weickert, Poisson noise removal using multi-frame 3D block matching, 2019 8th European Workshop on Visual Information Processing (EUVIP), Roma (2019) 58–63.

  13. Z. Ren, B. Zhao, W. Xu, P. Han and Y. Jiao, A convolution based path integration method approach to the damped parametric pendulum under different random noise excitations, Mech. Syst. Signal Process., 157 (2021) 107700.

    Article  Google Scholar 

  14. M. He, W. Xu, Z. Sun and L. Du, Characterization of stochastic resonance in a bistable system with Poisson white noise using statistical complexity measures, Commun. Nonlinear Sci., 28(1–3) (2015) 39–49.

    Article  MATH  Google Scholar 

  15. D. Huang, J. Yang, D. Zhou, G. Litak and H. Liu, Influence of Poisson white noise on the response statistics of nonlinear system and its applications to bearing fault diagnosis, J. Comput. Nonlinear Dyn., 14(3) (2019) 031010.

    Article  Google Scholar 

  16. Y. Chang, Y. Wang, T. Liu and Z. J. Wang, Fault diagnosis of a mine hoist using PCA and SVM techniques, J. China Univ. Min. Technol., 18(3) (2008) 327–331.

    Article  Google Scholar 

  17. Y. Kim, J. Park, K. Na, H. Yuan, B. D. Youn and C. Kang, Phase-based time domain averaging (PTDA) for fault detection of a gearbox in an industrial robot using vibration signals, Mech. Syst. Signal Process., 138 (2020) 106544.

    Article  Google Scholar 

  18. Z. Feng, M. Liang and F. Chu, Recent advances in time-frequency analysis methods for machinery fault diagnosis: a review with application examples, Mech. Syst. Signal Process., 38 (2013) 165–205.

    Article  Google Scholar 

  19. X. Zhang, Z. Liu, J. Wang and J. Wang, Time-frequency analysis for bearing fault diagnosis using multiple Q-factor Gabor wavelets, ISA Trans., 87 (2019) 225–234.

    Article  Google Scholar 

  20. G. Dong and J. Chen, Noise resistant time frequency analysis and application in fault diagnosis of rolling element bearings, Mech. Syst. Signal Process., 33 (2012) 212–236.

    Article  Google Scholar 

  21. J. Shi, M. Liang, D. S. Necsulescu and Y. Guan, Generalized stepwise demodulation transform and synchrosqueezing for time-frequency analysis and bearing fault diagnosis, J. Sound Vib., 368 (2016) 202–222.

    Article  Google Scholar 

  22. G. Yu, A concentrated time-frequency analysis tool for bearing fault diagnosis, IEEE Trans. Instrum. Meas., 69(2) (2019) 371–381.

    Article  Google Scholar 

  23. S. Lu, Q. He and J. Zhao, Bearing fault diagnosis of a permanent magnet synchronous motor via a fast and online order analysis method in an embedded system, Mech. Syst. Signal Process., 113 (2018) 36–49.

    Article  Google Scholar 

  24. A. Sapena-Bano, M. Pineda-Sanchez, R. Puche-Panadero, J. Perez-Cruz, J. Roger-Folch, M. Riera-Guasp and J. Martinez-Roman, Harmonic order tracking analysis: a novel method for fault diagnosis in induction machines, IEEE Trans. Energy Convers., 30(3) (2015) 833–841.

    Article  Google Scholar 

  25. J. Cheng, Y. Yang and D. Yu, The envelope order spectrum based on generalized demodulation time-frequency analysis and its application to gear fault diagnosis, Mech. Syst. Signal Process., 24 (2010) 508–521.

    Article  Google Scholar 

  26. R. Benzi, A. Sutera and A. Vulpiani, The mechanism of stochastic resonance, J. Phys. A Math. Theor., 14 (1981) L453.

    MathSciNet  Google Scholar 

  27. S. Lu, Q. He and J. Wang, A review of stochastic resonance in rotating machine fault detection, Mech. Syst. Signal Process., 116 (2019) 230–260.

    Article  Google Scholar 

  28. Z. Qiao, Y. Lei and N. Li, Applications of stochastic resonance to machinery fault detection: a review and tutorial, Mech. Syst. Signal Process., 122 (2019) 502–536.

    Article  Google Scholar 

  29. C. Yang, J. Yang, D. Zhou, S. Zhang and G. Litak, Adaptive stochastic resonance in bistable system driven by noisy NLFM signal: phenomenon and application, Philos. Trans. Royal Soc. A, 379(2192) (2021) 20200239.

    Article  MathSciNet  Google Scholar 

  30. J. Zhang, D. Huang, J. Yang, H. Liu and X. Liu, Realizing the empirical mode decomposition by the adaptive stochastic resonance in a new periodical model and its application in bearing fault diagnosis, J. Mech. Sci. Technol., 31(10) (2017) 4599–4610.

    Article  Google Scholar 

  31. J. Zhang, J. Yang, G. Litak and E. Hu, Feature extraction under bounded noise background and its application in low speed bearing fault diagnosis, J. Mech. Sci. Technol., 33(7) (2019) 3193–3204.

    Article  Google Scholar 

  32. T. Wang, M. Liang, J. Li and W. Cheng, Rolling element bearing fault diagnosis via fault characteristic order (FCO) analysis, Mech. Syst. Signal Process., 45 (2014) 139–153.

    Article  Google Scholar 

  33. J. Sun, B. Feng and W. Xu, Particle swarm optimization with particles having quantum behavior, Proceedings of the 2004 Congress on Evolutionary Computation, 1 (2004) 325–331.

    Article  Google Scholar 

  34. Z. Feng, X. Chen and T. Wang, Time-varying demodulation analysis for rolling bearing fault diagnosis under variable speed conditions, J. Sound Vib., 400 (2017) 71–85.

    Article  Google Scholar 

Download references

Acknowledgments

This project is supported by the Major Special Basic Research Projects of Aeroengine and Gas Turbine (Grant No. 2017-IV-0008-0045), China.

Author information

Authors and Affiliations

  1. Department of Mechanics, Tianjin University, Tianjin, 300354, China

    Qiang Ma & Shuqian Cao

  2. College of Mechanical and Equipment Engineering, Hebei University of Engineering, Handan, 056038, China

    Qiang Ma

  3. Key Laboratory of Intelligent Industrial Equipment Technology of Hebei Province (Hebei University of Engineering), Handan, 056038, China

    Qiang Ma

  4. Jiangsu Key Laboratory of Mine Mechanical and Electrical Equipment, School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou, 221116, China

    Tao Gong & Jianhua Yang

Authors
  1. Qiang Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shuqian Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tao Gong
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jianhua Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shuqian Cao.

Additional information

Qiang Ma received the B.S. degree in Mechanical and Electrical Engineering from Hebei Institute of Architecture and Technology in 2002, and a Master’s degree in Industrial Engineering from Hebei University of Engineering in 2010. He is currently pursuing a Doctorate degree in the School of Mechanical Engineering of Tianjin University since 2018. He has been an Associate Professor of Mechanical Engineering at Hebei University of Engineering, Handan City, Hebei province, China. He has published more than 10 papers in journals sponsored by IEEE, SAGE, ASME and other academic institutions. His main research interests include R&D and manufacturing of mechanical and electrical equipment, intelligent monitoring and fault diagnosis of mechanical systems.

Shuqian Cao who received his Ph.D. in Dynamics and Control from Tianjin University, is currently a Professor of Mechanics in the School of Mechanical Engineering, Tianjin University. He is now the Director of Tianjin Key Laboratory of Nonlinear Dynamics and Control, Council Member of Chinese Society for Vibration Engineering (CSVE). His research effort is focused on machine and structure dynamics, especially on the theory and applications of nonlinear dynamics in rotary machines, covering the fields of aero-engines, gas turbines and combustion engines. He and his co-workers have published over 100 papers and 3 books.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ma, Q., Cao, S., Gong, T. et al. Weak fault feature extraction of rolling bearing under strong poisson noise and variable speed conditions. J Mech Sci Technol 36, 5341–5351 (2022). https://doi.org/10.1007/s12206-022-1001-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-022-1001-1

Keywords

Search

Navigation