Skip to main content
SpringerLink
Log in

Mechanical characteristics and experimental research of a flexible rope-sheave hoisting mechanism

  • Original Article
  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

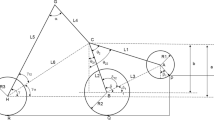
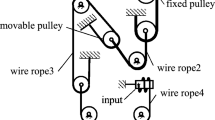
Owing to such advantages as long transmission distances and compact structures, flexible rope-sheave lifting mechanisms are important for applications in disaster relief, emergency treatment, high-altitude operations, and robot transmission. Despite their long research history and wide range of applications, the mechanical properties of the interactions between flexible ropes and sheaves have been investigated by few studies, most of which rely on experience and experimental test results for design. The present study developed a mathematical model for the mechanical characteristics of a hoisting mechanism that was composed of a sheave with gear teeth, pressure wheels, and a flexible rope. The critical value for the hoisting mechanism’s slippage was analyzed, and the parameters that affected the lifting performance, such as the sheave groove angle and gear teeth, were simulated and optimized. The results were consistent with the experimental test data. The optimized rope-sheave lifting mechanism was further applied to the design and development of rope-climbing robots, and its lifting performance was experimentally tested. The research results presented in this paper described the mechanical characteristics of the flexible rope-sheave lifting mechanism, combined the mechanical model with the optimized design, and verified them through experiments; this provided guidance for more precise and quantitative applications of flexible rope-sheaves.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

τ :

The rope-sheave teeth of the front face angle (°)

β :

The angle between the x(′-axis and the x1-axis ((°)

ρ :

The distance from any point to the specified point on the contact surface (mm)

ϕ :

The groove angle of the rope-sheave (°)

θ :

The rope-sheave wrap angle (°)

θ s :

The sliding angle (°)

θ r :

The static angle (°)

dl :

The micro-arc (mm)

dF Y :

The positive pressure on the rope micro-segment (N)

dF a :

The tight-edge tension increment (N)

References

  1. S. Schmidt and K. Berns, Climbing robots for maintenance and inspections of vertical structures—a survey of design aspects and technologies, Robotics and Autonomous Systems, 61(12) (2013) 1288–1305.

    Article  Google Scholar 

  2. T. Schober, CLIBOT -ein seilkletternder Roboter zur Bauwerksin-spektion, Bautechnik, 87(2) (2010) 81–85.

    Article  Google Scholar 

  3. B. Chu et al., A survey of climbing robots: Locomotion and adhe-sion, International Journal of Precision Engineering and Manu-Facturing, 11(4) (2010) 633–647.

    Article  Google Scholar 

  4. Y. Guo et al., Experimental research on effect of wire rope trans-verse vibration on friction transmission stability in a friction hoist-ing system, Tribology International, 115 (2017) 233–245.

    Article  Google Scholar 

  5. J. Yao et al., Assessment of safety for axial fluctuations of head sheaves in mine hoist based on coupled dynamic model, Engineering Failure Analysis, 51 (2015) 98–107.

    Article  Google Scholar 

  6. K. Seo et al., Design and stability analysis of a novel wall-climbing robotic platform (ROPE RIDE), Mechanism and Machine Theory, 70 (2013) 189–208.

    Article  Google Scholar 

  7. P. R. Ratanghayra, A. A. Hayat and S. K. Saha, Design and Analysis of Spring-Based Rope Climbing Robot, Singapore: Springer Singapore (2019).

    Book  Google Scholar 

  8. S. Yu et al., Design and analysis of a modular rope-climbing robot with the finger-wheeled mechanism, Journal of Mechanical Science and Technology, 35(5) (2021) 2197–2207.

    Article  Google Scholar 

  9. S. Yoo, T. Kim, M. Seo, J. Oh, H. S. Kim and T. Seo, Position-tracking control of dual-rope winch robot with rope slip compensation, IEEE/ASME Transactions on Mechatronics, 26(4) (2021) 1754–1762.

    Article  Google Scholar 

  10. B. Song et al., Dynamic simulation and optimization of clamping mechanism of online tension testing machine for wire ropes, Engineering Failure Analysis, 95 (2019) 181–190.

    Article  Google Scholar 

  11. P. Davies et al., An empirical model to predict the lifetime of braided HMPE handling ropes under cyclic bend over sheave (CBOS) loading, Ocean Engineering, 97 (2015) 74–81.

    Article  Google Scholar 

  12. W. Huang et al., Modeling nonlinear time-dependent behaviors of synthetic fiber ropes under cyclic loading, Ocean Engineering, 109 (2015) 207–216.

    Article  Google Scholar 

  13. V. A. Lubarda, Determination of the belt force before the gross slip, Mechanism and Machine Theory, 83 (2015) 31–37.

    Article  Google Scholar 

  14. X. Gao, L. Wang and X. Hao, An improved Capstan equation including power-law friction and bending rigidity for high performance yarn, Mechanism and Machine Theory, 90 (2015) 84–94.

    Article  Google Scholar 

  15. T. Morimoto and H. Iizuka, Rolling contact between a rubber ring and rigid cylinders: mechanics of rubber belts, International Journal of Mechanical Sciences, 54(1) (2012) 234–240.

    Article  Google Scholar 

  16. B. Balta, F. O. Sonmez and A. Cengiz, Speed losses in V-ribbed belt drives, Mechanism and Machine Theory, 86 (2015) 1–14.

    Article  Google Scholar 

  17. L. Della Pietra and F. Timpone, Tension in a flat belt transmission: experimental investigation, Mechanism and Machine Theory, 70 (2013) 129–156.

    Article  Google Scholar 

  18. M., M. et al., Measurement of the cable-pulley Coulomb and viscous friction for a cable-driven surgical robotic system, 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (2015).

  19. V. Varlamov, On the spatially two-dimensional Boussinesq equation in a circular domain, Nonlinear Analysis: Theory, Methods and Applications, 46(5) (2001) 699–725.

    Article  MathSciNet  Google Scholar 

  20. S. Mesloub and H. E. Gadain, On Some Initial and Initial Boundary Value Problems for Linear and Nonlinear Boussinesq Models, Symmetry, 11(10) (2019) 1273.

    Article  Google Scholar 

Download references

Acknowledgments

This work was supported by the Program for Innovative Research Team in Universities of the Inner Mongolia Autonomous Region (Grant No. NMGIRT2213), the National Key R&D Program of China (Grant No. 2018YFB1307501), the National Natural Science Foundation of China (Grant No. 61763036), the Natural Science Foundation of Inner Mongolia (Grant No. 2021MS05005), and the Key Technology Research Program of Inner Mongolia (Grant No. 2021GG0258). This support is gratefully acknowledged by the authors.

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Inner Mongolia University of Technology, Hohhot, 010051, China

    Shufeng Tang, Renjie Huang & Guoqing Zhao

  2. Inner Mongolia Key Laboratory of Special Service Intelligent Robotics, Hohhot, 010051, China

    Shufeng Tang, Renjie Huang & Guoqing Zhao

Authors
  1. Shufeng Tang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Renjie Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Guoqing Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shufeng Tang.

Additional information

Shufeng Tang received the Ph.D. degree in Mechanical Engineering in Harbin Institute of Technology, China, in 2010. He is currently a Professor with the School of Mechanical Engineering, Inner Mongolia University of Technology. His current research interests focus on robot technology and extreme environment special equipment technology.

Renjie Huang is a graduate student of the School of Mechanical Engineering of Inner Mongolia University of Technology in China. He received a bachelor’s degree from Inner Mongolia University of Technology. His research interests include robotic design and optimization design.

Guoqing Zhao is a graduate student at the School of Mechanical Engineering of Inner Mongolia University of Technology in China. He received a bachelor’s degree from North China University of Water Resources and Electric Power. His research interests include micro-robot technology and dynamic simulation.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tang, S., Huang, R. & Zhao, G. Mechanical characteristics and experimental research of a flexible rope-sheave hoisting mechanism. J Mech Sci Technol 36, 3329–3339 (2022). https://doi.org/10.1007/s12206-022-0612-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-022-0612-x

Keywords

Search

Navigation