Skip to main content
SpringerLink
Log in

Operational transfer path analysis based on deep neural network: Numerical validation

  • Original Article
  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

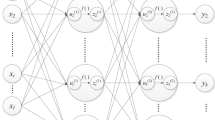
Abstract

In this study, a novel transfer path analysis formulation using an emerging deep neural network model is presented and numerically validated for a multi-structural system. In the proposed formulation, only the operational responses of structures are utilized to identify the contributions of all paths to vibration responses at a point of interest in the frequency domain. To this end, the model parameters of a dense neural network model are initially determined using a training dataset to predict the responses precisely. Next, the contribution of each path is identified from the responses predicted by using the trained network model with the input associated with the selected path eliminated. To establish the correct model, the original operational datasets are augmented using the phase shift and the cross-spectrum. The path contributions estimated using the proposed formulation with another numerically generated operational dataset are compared with the known path contributions. The comparison results show that the proposed method based on a deep neural network model can successfully predict the path contributions using only operational responses.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

B :

Constant vector added to nodes in the DNN

C nm :

Contribution of m-th input on the n-th ROI

c m :

Contribution of m-th input on the ROI

H :

Number of hidden layers + 1

J 0 :

Number of measured training datasets

J 1 :

Number of phases generated for phase augmentation

M :

Number of input

N :

Number of output

P :

Number of nodes in the DNN

R :

ROI in a system

R̃ :

Predicted ROI by the DNN

R̄ j :

Predicted ROI by putting the j-th input to zero

R̿ j :

Predicted ROI by putting all zeros except j-th input

R̆ :

Measured ROI

S :

Covariance matrix

T :

Transfer function matrix for a subsystem

T nm :

A transfer function for the m-th input and n-th ROI

U :

Input vector of the DNN

(U, Y):

Element of training dataset

W :

Weight matrix multiplied by the variables of nodes in the DNN

X :

Input response vector in a system

X̄ j :

Input vector with the j-th input to zero

X̿ j :

Input vector with all zeros except for the j-th input

X̆ :

Measured input response

Y :

Output vector of the DNN

Ỹ :

Predicted output vector with current model parameters

Z :

Hidden variable vector in the DNN

ℵ:

Training dataset

ℵ0 :

Initial datasets from measurements

ℵ1 :

Phase augmented training datasets

ℵ2 :

Cross-spectrum augmented training datasets by input

ℵ3 :

Cross-spectrum augmented training datasets by output

ϕ :

Phase of a response

θ̂ :

Trained model parameters

θ :

Model parameters for the DNN

θ̂ :

Trained model parameters

‖·‖:

Norm of a vector

x* :

Complex conjugate of a complex variable x

References

  1. F. Magrans, P. Rodriguez and G. Cousin, Low and mid-high frequency advanced transmission path analysis, Proceedings of the Twelfth International Congress on Sound and Vibration ICSV12 (2005).

    Google Scholar 

  2. M. V. van der Seijs, D. de Klerk and D. J. Rixen, General framework for transfer path analysis: History, theory and classification of techniques, Mechanical Systems and Signal Processing, 68 (2016) 217–244.

    Article  Google Scholar 

  3. A. Diez-Ibarbia, M. Battarra, J. Palenzuela, G. Cervantes, S. Walsh, M. De-la-Cruz, S. Theodossiades and L. Gagliardini, Comparison between transfer path analysis methods on an electric vehicle, Applied Acoustics, 118 (2017) 83–101.

    Article  Google Scholar 

  4. J. W. Verheij, Multi-path sound transfer from resiliently mounted shipboard machinery: Experimental methods for analyzing and improving noise control, Thesis, Delft University of Technology (1982).

    Google Scholar 

  5. A. Thite and D. Thompson, The quantification of structure-borne transmission paths by inverse methods. Part 1: Improved singular value rejection methods, Journal of Sound and Vibration, 264 (2) (2003) 411–431.

    Article  Google Scholar 

  6. A. S. Elliott, A. T. Moorhouse, T. Huntley and S. Tate, In-situ source path contribution analysis of structure borne road noise, Journal of Sound and Vibration, 332 (24) (2013) 6276–6295.

    Article  Google Scholar 

  7. B. Petersson and B. Gibbs, Towards a structure-borne sound source characterization, Applied Acoustics, 61 (3) (2000) 325–343.

    Article  Google Scholar 

  8. J. Mondot and B. Petersson, Characterization of structure-borne sound sources: The source descriptor and the coupling function, Journal of Sound and Vibration, 114 (3) (1987) 507–518.

    Article  Google Scholar 

  9. A. Moorhouse, A. Elliott and T. Evans, In situ measurement of the blocked force of structure-borne sound sources, Journal of Sound and Vibration, 325 (4–5) (2009) 679–685.

    Article  Google Scholar 

  10. M. Janssens and J. Verheij, A pseudo-forces methodology to be used in characterization of structure-borne sound sources, Applied Acoustics, 61 (3) (2000) 285–308.

    Article  Google Scholar 

  11. M. H. Janssens, J. W. Verheij and D. Thompson, The use of an equivalent forces method for the experimental quantification of structural sound transmission in ships, Journal of Sound and Vibration, 226 (2) (1999) 305–328.

    Article  Google Scholar 

  12. B. Petersson and B. Gibbs, Use of the source descriptor concept in studies of multi-point and multi-directional vibrational sources, Journal of Sound and Vibration, 168 (1) (1993) 157–176.

    Article  Google Scholar 

  13. D. Lennström, M. Olsson, F. Wullens and A. Nykänen, Validation of the blocked force method for various boundary conditions for automotive source characterization, Applied Acoustics, 102 (2016) 108–119.

    Article  Google Scholar 

  14. J. Yoshida and K. Tanaka, Contribution analysis of vibration mode utilizing operational TPA, Mechanical Engineering Journal, 3 (1) (2016) 15-00589-00515-00589.

    Google Scholar 

  15. O. Guasch, C. García, J. Jové and P. Artís, Experimental validation of the direct transmissibility approach to classical transfer path analysis on a mechanical setup, Mechanical Systems and Signal Processing, 37 (1–2) (2013) 353–369.

    Article  Google Scholar 

  16. P. Gajdatsy, K. Janssens, W. Desmet and H. Van der Auweraer, Application of the transmissibility concept in transfer path analysis, Mechanical Systems and Signal Processing, 24 (7) (2010) 1963–1976.

    Article  Google Scholar 

  17. D. De Klerk and A. Ossipov, Operational transfer path analysis: Theory, guidelines and tire noise application, Mechanical Systems and Signal Processing, 24 (7) (2010) 1950–1962.

    Article  Google Scholar 

  18. M. Lohrmann and T. Hohenberger, Operational transfer path analysis: comparison with conventional methods, Journal Article, 123 (5) (2008) 3534.

    Google Scholar 

  19. K. Noumura and J. Yoshida, Method of transfer path analysis for vehicle interior sound with no excitation experiment, Proceedings of FISITA2006 (2006) 1–10.

    Google Scholar 

  20. O. Guasch and F. Magrans, The global transfer direct transfer method applied to a finite simply supported elastic beam, Journal of Sound and Vibration, 276 (1–2) (2004) 335–359.

    Article  Google Scholar 

  21. A. Ribeiro, J. Silva and N. Maia, On the generalisation of the transmissibility concept, Mechanical Systems and Signal Processing, 14 (1) (2000) 29–35.

    Article  Google Scholar 

  22. A. Oktav, Ç. Yılmaz and G. Anlaş, Transfer path analysis: Current practice, trade-offs and consideration of damping, Mechanical Systems and Signal Processing, 85 (2017) 760–772.

    Article  Google Scholar 

  23. A. Krizhevsky, I. Sutskever and G. E. Hinton, Imagenet classification with deep convolutional neural networks, Advances in Neural Information Processing Systems (2012) 1097–1105.

    Google Scholar 

  24. D. C. Ciresan, U. Meier, J. Masci, L. M. Gambardella and J. Schmidhuber, Flexible, high performance convolutional neural networks for image classification, Twenty-Second International Joint Conference on Artificial Intelligence (2011).

    Google Scholar 

  25. J. Chung, C. Gulcehre, K. Cho and Y. Bengio, Empirical evaluation of gated recurrent neural networks on sequence modeling, arXiv preprint arXiv:1412.3555 (2014).

    Google Scholar 

  26. S. Hochreiter and J. Schmidhuber, Long short-term memory, Neural Computation, 9 (8) (1997) 1735–1780.

    Article  Google Scholar 

  27. D. J. Rezende, S. Mohamed and D. Wierstra, Stochastic backpropagation and approximate inference in deep generative models, arXiv preprint arXiv:1401.4082 (2014).

    Google Scholar 

  28. D. P. Kingma and M. Welling, Auto-encoding variational bayes, arXiv preprint arXiv:1312.6114 (2013).

    Google Scholar 

  29. I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville and Y. Bengio, Generative adversarial nets, Advances in Neural Information Processing Systems (2014) 2672–2680.

    Google Scholar 

  30. C. Francois, Deep Learning with Python, Manning Publications Company (2017).

    Google Scholar 

  31. D. Lee, Y.-D. Kim, N.-Y. Lee and S.-W. Lee, On joint mobility design in multi-structural systems, Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 230 (6) (2016) 817–829.

    Google Scholar 

  32. D. N. Herting, MSC/NASTRAN Advanced Dynamic Analysis User’s Guide (1997).

    Google Scholar 

  33. F. Chollet, Keras: The Python Deep Learning Library, Astrophysics Source Code Library (2018).

    Google Scholar 

  34. T. Tieleman and G. Hinton, Rmsprop: Divide the gradient by a running average of its recent magnitude. coursera, Neural Networks for Machine Learning, Technical Report (2012) 31.

    Google Scholar 

Download references

Acknowledgments

This work was supported by a grant from the National Research Foundation of Korea (NRF) funded by the Korean government (MEST; Grant No. NRF-2018R1A2B2005391). This work was also partially supported by the Korea Basic Science Institute (KBSI) National Research Facilities & Equipment Center (NFEC) grant funded by the Korea government (Ministry of Education) (No. 2019R1A6C1010045).

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Dongeui University, Busan, 47340, Korea

    Dooho Lee

  2. Department of Mechanical Engineering, Ajou University, Suwon-si, 16499, Korea

    Jin Woo Lee

Authors
  1. Dooho Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jin Woo Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dooho Lee.

Additional information

Recommended by Editor No-cheol Park

Dooho Lee received his B.S. degree from Seoul National University (Korea) in 1988, his M.S. from KAIST (Korea) in 1990, and his Ph.D. from KAIST (Korea) in 1994. He worked for Samsung Motors, Inc. (1995-1999) and is currently a Professor at Dongeui University. His research focuses on the design optimization of structural-acoustic systems, uncertainty propagation in dynamic problems, and sound transfer characteristics in human hearing systems.

Jin Woo Lee has been a Professor of Mechanical Engineering at Ajou University since 2009. His research interests are in the area of vibration, acoustics, acoustic and vibration metamaterials, topology optimization based designs and fluid-structure interactions of micro-cantilevers for RF-MEMS and AFM. His Ph.D. is from the School of Mechanical and Aerospace Engineering from Seoul National University in South Korea in 2003. He worked with Samsung Electronics Company from 2003 to 2006 and studied as a post-doctoral research associate at Seoul National University from 2006 to 2007. From 2007 to 2009, he was a postdoctoral research associate of Mechanical Engineering at Purdue University, West Lafayette, IN, USA.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lee, D., Lee, J.W. Operational transfer path analysis based on deep neural network: Numerical validation. J Mech Sci Technol 34, 1023–1033 (2020). https://doi.org/10.1007/s12206-020-0205-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-020-0205-5

Keywords

Search

Navigation