Skip to main content
SpringerLink
Log in

Comments on the stability of the synchronous states of three vibrators in a vibrating system with two rigid frames

  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

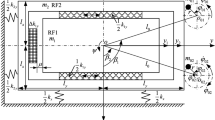
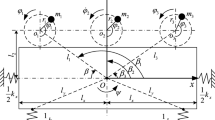
This paper focuses on the stability of three homodromy vibrators in a vibrating system with two rigid frames (RFs). The motion differential equations of the system are established. Using the average method yields the average coupling torque balanced equations of three vibrators, and the simplified analytical expressions for synchronization and stability criterions of the system were derived. The coupling dynamic characteristics were numerically analyzed, including frequency-amplitude response, stable phase differences, synchronization and stability ability, and phase relationships. The simulations to verify the validity of theoretical results were carried out. It is shown that the stable states of the system are classified into three types, thereof the stability of phase differences among vibrators is similar in sub-resonant and super-resonant states, which results in no vibration of the system. While in near sub-resonant state the system reflects strong useful positive superposition vibration with energy saving, which is exactly the desire in engineering design.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

f 0 i :

Damping coefficient of the induction motor i, i = 1, 2, 3

f jx :

Damping constant of the RF j in x-direction, j = 1, 2

k jx :

Stiffness of the spring in x-direction, i = 1, 2, 3

m 1 :

Mass of the RF1

m 2 :

Mass of the RF2

m 0 :

Mass of the standard vibrator

m 0 i :

Mass of the vibrator i, m0i = m0, i = 1, 2, 3

m :

Induced mass of the vibrating system, m = M′1M′2/(M′1+ M′2), M′1 ≈ M1, M′2 = M2

M :

Mass of the total vibrating system, M = M1 + M2, M1 = m1, M2 = m2 + m01 + m02 + m03

r i :

Eccentric radius of three vibrators, ri = r, i = 1, 2, 3

r m :

Mass ratio between the standard vibrator and the total vibrating system, rm = m0/M

r m1 :

Mass ratio between the RF1 and the total system, rm1 = M1/M

r m2 :

Mass ratio between the standard vibrator and the RF2, rm2 = m0/M2

T ei :

Electromagnetic torque of the induction motor i, i = 1, 2, 3

T e0 i :

Electromagnetic torque of the induction motor i operating steadily, i = 1, 2, 3

z i :

Frequency ratio between the operating frequency and natural frequencies, zi = ωm0/ωi, i = 0, 1

ω m0 :

Synchronous angular velocity of three vibrators when the induction motors operate steadily

ω 1 :

Natural frequency of the RF1, \({\omega _1} = \sqrt {\left( {{k_{1x}} + {k_{2x}}} \right)/{M_1}} \)

ω 0 :

Natural frequency of the main vibrating system, \({\omega _0} = \sqrt {{k_{2x}}/m} \)

ω g :

Natural frequency of the isolated vibrating system, \({\omega _g} = \sqrt {{k_{1x}}/M} \)

γ jx :

Phase lag angle of the RF j in x-direction, j = 1, 2

ξ jx :

Critical damping ratio of the RF j in x-direction, j = 1, 2

η i :

Mass ratio between the vibrator i and the standard vibrator, ηi = m0i/m0, i = 1, 2, 3

\((\dot \bullet )\) :

d ● /dt

\((\ddot \bullet )\) :

d2 ● /dt2

References

  1. J. Rayleigh and J. W. Strutt, The Theory of Sound, Dover, London (1877).

    MATH  Google Scholar 

  2. C. Zhou, Y. B. Liu and X. M. Rui, Mechanism and characteristic of rain-induced vibration on high-voltage transmission line, J. of Mechanical Science and Technology, 26 (8) (2012) 2505–2510.

    Article  Google Scholar 

  3. M. Kapitaniak et al., Synchronization of clocks, Physics Reports, 517 (2012) 1–69.

    Article  Google Scholar 

  4. G. V. Osipov, J. Kurths and C. S. Zhou, Synchronization in Oscillatory Networks, Springer, Berlin Heidelberg (2007).

    Book  Google Scholar 

  5. R. Yamapi and P. Woafo, Dynamics and synchronization of coupled self-sustained electromechanical devices, J. of Sound and Vibration, 285 (2005) 1151–1170.

    Article  Google Scholar 

  6. J. A. Acebrón et al., The Kuramoto model: A simple paradigm for synchronization phenomena, Reviews of Modern Physics, 77 (1) (2005) 137–185.

    Article  MathSciNet  Google Scholar 

  7. P. Perlikowski, A. Stefański and T. Kapitaniak, 1:1 mode locking and generalized synchronization in mechanical oscillators, J. of Sound and Vibration, 318 (2008) 329–340.

    Article  Google Scholar 

  8. H. A. Tanaka, A. J. Lichtenberg and S. Oishi, Self-synchronization of coupled oscillators with hysteretic responses, European Physical J. D, 100 (1997) 279–300.

    MATH  Google Scholar 

  9. I. I. Blekhman, Vibrational Mechanics, World Scientific, Singapore (1988).

    MATH  Google Scholar 

  10. I. I. Blekhman et al., On self-synchronization and controlled synchronization, Systems & Control Letters, 31 (5) (1997) 299–305.

    Article  MathSciNet  Google Scholar 

  11. I. I. Blekhman et al., Self-synchronization and controlled synchronization: General definition and example design, Mathematics and Computers in Simulation, 58 (2002) 367–384.

    Article  MathSciNet  Google Scholar 

  12. I. I. Blekhman and V. S. Sorokin, On the separation of fast and slow motions in mechanical systems with high-frequency modulation of the dissipation coefficient, J. of Sound and Vibration, 329 (23) (2010) 4936–4949.

    Article  Google Scholar 

  13. J. Inoue and Y. Araki, Self-synchronization of mechanical system (multiple cycle), Proceedings of Japanese Mechanical Engineering Society, 42 (1981) 103–110 (in Japanese).

    Google Scholar 

  14. B. C. Wen et al., Vibratory Synchronization and Controlled Synchronization in Engineering, Science Press, Beijing (2009).

    Google Scholar 

  15. B. C. Wen et al., Theory and techniques of vibrating machinery and their applications, Science Press, Beijing (2010).

    Google Scholar 

  16. J. M. Balthazar, J. L. P. Felix and R. M. Brasil, Short comments on self-synchronization of two non-ideal sources supported by a flexible portal frame structure, J. of Vibration and Control, 10 (12) (2004) 1739–1748.

    Article  Google Scholar 

  17. J. M. Balthazar, J. L. P. Felix and R. M. Brasil, Some comments on the numerical simulation of self-synchronization of four non-ideal exciters, Applied Mathematics and Computation, 164 (2) (2005) 615–625.

    Article  MathSciNet  Google Scholar 

  18. A. Teufel, A. Steindl and H. Troger, Synchronization of two flow excited pendula, Communications in Nonlinear Science and Numerical Simulation, 11 (5) (2006) 577–594.

    Article  MathSciNet  Google Scholar 

  19. P. Fang and Y. J. Hou, Synchronization characteristics of a rotor-pendula system in multiple coupling resonant systems, Proceedings of the Institution of Mechanical Engineers, Part C: J. of Mechanical Engineering Science, 232 (10) (2017) 1802–1822.

    Google Scholar 

  20. P. Fang et al., Study of synchronization for a rotor-pendulum system with poincare method, J. of Vibroengineering, 17 (5) (2015) 2681–2695.

    Google Scholar 

  21. X. L. Zhang, B. C. Wen and C. Y. Zhao, Vibratory synchronization transmission of a cylindrical roller in a vibrating mechanical system excited by two exciters, Mechanical Systems and Signal Processing, 96 (2017) 88–103.

    Article  Google Scholar 

  22. X. L. Zhang, B. C. Wen and C. Y. Zhao, Vibratory synchronization transmission of two exciters in a super-resonant vibrating system, J. of Mechanical Science and Technology, 28 (6) (2014) 2049–2058.

    Article  Google Scholar 

  23. X. L. Zhang et al., Synchronous stability of four homodromy vibrators in a vibrating system with double resonant types, Shock and Vibration (2018) Article ID 9641231, 20.

  24. C. Y. Zhao et al., Synchronization of two non-identical coupled exciters in a non-resonant vibrating system of linear motion part I: theoretical analysis, Shock and Vibration, 16 (5) (2009) 505–516.

    Article  Google Scholar 

Download references

Acknowledgments

This work was supported by the National Natural Science Foundations of China [grant number 51675090], the Fundamental Research Funds for the Central Universities [grant number N170304013] and China Postdoctoral Science Foundation [grant number 2017M621145].

Author information

Authors and Affiliations

  1. School of Mechanical Engineering and Automation, Northeastern University, Shenyang, Liaoning, 110819, China

    Xueliang Zhang, Zhihui Wang, Chao Li & Jinlin Xu

  2. Northern Heavy Industries Group, State Key Laboratory of Tunnel Boring Machine, Shenyang, Liaoning, 110141, China

    Xueliang Zhang

Authors
  1. Xueliang Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhihui Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chao Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jinlin Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xueliang Zhang.

Additional information

Recommended by Associate Editor Dongho Oh

Xueliang Zhang received his Ph.D. from Northeastern University, Shenyang, China. He is currently an Associate Professor in the School of Mechanical Engineering and Automation, Northeastern University, China. His research interests include synchronization theory, vibration utilization engineering, and nonlinear vibration in engineering.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, X., Wang, Z., Li, C. et al. Comments on the stability of the synchronous states of three vibrators in a vibrating system with two rigid frames. J Mech Sci Technol 33, 4659–4672 (2019). https://doi.org/10.1007/s12206-019-0909-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-019-0909-6

Keywords

Search

Navigation