Abstract
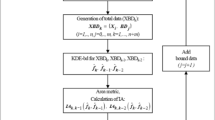
Uncertainty quantification, which identifies a probabilistic distribution for uncertain data, is important for yielding accurate and reliable results in reliability analysis and reliability-based design optimization. Sufficient data are needed for accurate uncertainty quantification, but data is very limited in engineering fields. For statistical modeling using insufficient data, kernel density estimation (KDE) with estimated bounded data (KDE-ebd) has been recently developed for more accurate and conservative estimation than the original KDE by combining given data and bounded data within estimated intervals of random variables from the given data. However, the estimated density function using KDE-ebd is modeled beyond the domain of random variables due to conservative estimation of the density function with long and thick tails. To overcome this problem, this paper proposes kernel density estimation with hybrid estimated bounded data (KDE-Hebd), which does not violate the domain of the random variables, and uses point or interval estimation of the bounds for generating the bounded data. KDE-ebd often yields too wide bounds for very insufficient data or large variations because it uses only the estimated intervals of random variables. The proposed KDE with hybrid estimated bounded data alternatively selects a point estimator or interval estimator according to whether the estimated intervals violate the domain of the random variables. The performance of the proposed method was evaluated by comparing the estimation accuracy from statistical simulation tests for mathematically derived sample data and real experimental data using KDE, KDE-ebd and KDE-Hebd. As a result, it was demonstrated that KDE-Hebd was more accurate than KDE-ebd without the violation of the domain of random variables, especially for a large coefficient of variation.
Similar content being viewed by others
References
P. E. Hess, D. Bruchman, I. A. Assakkaf and B. M. Ayyub, Uncertainties in material and geometric strength and load variables, Naval Engineers Journal, 114 (2) (2002) 139–166.
M. Lukić and C. Cremona, Probabilistic assessment of welded joints versus fatigue and fracture, Journal of Structural Engineering, 127 (2) (2001) 211–218.
Y. Noh, K. K. Choi and I. Lee, Identification of marginal and joint CDFs using Bayesian method for RBDO, Structural and Multidisciplinary Optimization, 40 (1) (2010) 35–51.
Q. Jiwei, Z. Jianguo and M. Yupeng, Reliability analysis based on the principle of maximum entropy and Dempster–Shafer evidence theory, Journal of Mechanical Science and Technology, 32 (2) (2018) 605–613.
C. K. Choi and H. H. Yoo, Uncertainty analysis of nonlinear systems employing the first–order reliability method, Journal of Mechanical Science and Technology, 26 (1) (2012) 39–44.
B. C. Jung, D. Lee, B. D. Youn and S. Lee, A statistical characterization method for damping material properties and its application to structural–acoustic system design, Journal of Mechanical Science and Technology, 25 (8) (2011) 1893–1904.
Y. J. Kang, O. K. Lim and Y. Noh, Sequential statistical modeling method for distribution type identification, Structural and Multidisciplinary Optimization, 54 (6) (2016) 1587–1607.
Y. J. Kang, J. Hong, O. K. Lim and Y. Noh, Reliability analysis using parametric and nonparametric input modeling methods, Journal of the Computational Structural Engineering Institute of Korea, 30 (1) (2017) 87–94.
F. Zhang, Y. Liu, C. Chen, Y. F. Li and H. Z. Haung, Fault diagnosis of rotating machinery based on kernel density estimation and Kullback–Leibler divergence, Journal of Mechanical Science and Technology, 28 (11) (2014) 4441–4454.
S. G. Cho, J. Jang, S. Kim, S. Park, T. H. Lee, M. Lee and S. Hong, Nonparametric approach for uncertainty–based multidisciplinary design optimization considering limited data, Structural and Multidisciplinary Optimization, 54 (6) (2016) 1671–1688.
J. Jang, S. G. Cho, S. J. Lee, K. S. Kim, J. M. Kim, J. P. Hong and T. H. Lee, Reliability based robust design optimization with kernel density estimation for electric power steering motor considering manufacturing uncertainties, IEEE Transaction on Magnetics, 51 (3) (2015) 1–4.
Y. J. Kang, Y. Noh and O. K. Lim, Kernel density estimation with bounded data, Structural and Multidisciplinary Optimization, 57 (1) (2018) 95–113.
B. W. Silverman, Density estimation for statistics and data analysis, CRC press, London, 26 (1986).
M. P. Wand and M. C. Jones, Kernel smoothing, CRC press, London (1994).
S. Chen, Optimal bandwidth selection for kernel density functionals estimation, Journal of Probability and Statistics, 2015 (2015) 1–21.
A. C. Guidoum, Kernel estimator and bandwidth selection for density and its derivatives, Department of Probabilities & Statistics, Faculty of Mathematics, University of Science and Technology Houari Boumediene, Algeria, https://cran.rproject. org/web/packages/kedd/vignettes/kedd.pdf (2015).
B. E. Hansen, Lecture notes on nonparametrics, University of Wisconsin–Madison, WI, USA, http://www.ssc.wisc.edu/~bhansen/718/NonParametrics1.pdf (2009).
S. J. Sheather, Density estimation, Statistical Science, 19 (4) (2004) 588–597.
J. H. Jung, Y. J. Kang, O. K. Lim and Y. Noh, A new method to determine the number of experimental data using statistical modeling methods. Journal of Mechanical Science and Technology, 31 (6) (2017) 2901–2910.
J. W. Tukey, Exploratory data analysis, Pearson, New York (1977).
M. Frigge, D. C. Hoaglin and B. Lglewicz, Some implementations of the boxplot, The American Statistician, 43 (1) (1989) 50–54.
D. Socie, Probabilistic statistical simulations technical background, eFatigue LLC (2008) https://www.efatigue. com/probabilistic/background/strainlife.html, April (2014).
D. C. Montgomery and G. C. Runger, Applied statistics and probability for engineers, 3rd Ed., Wiley, New York (2003).
Author information
Authors and Affiliations
Corresponding author
Additional information
Recommended by Associate Editor Byeng Dong Youn
Young-Jin Kang received his Ph.D. degree in School of Mechanical Engineering from Pusan National University in 2018. He is currently a postdoctoral researcher in School of Mechanical Engineering at Pusan National University. His research area is uncertainty quantification, reliability analysis, and design under uncertainties.
Yoojeong Noh is an Assistant Professor in School of Mechanical Engineering of Pusan National University. Her research area is uncertainty quantification and design under uncertainties.
Rights and permissions
About this article
Cite this article
Kang, YJ., Noh, Y. & Lim, OK. Development of a kernel density estimation with hybrid estimated bounded data. J Mech Sci Technol 32, 5807–5815 (2018). https://doi.org/10.1007/s12206-018-1128-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12206-018-1128-2