Skip to main content
SpringerLink
Log in

Control of an electromechanical pendulum subjected to impulsive disturbances using the Melnikov theory approach

  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

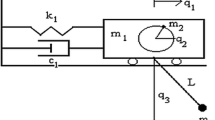
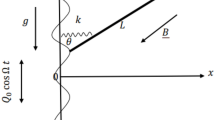
The dynamics of an electromechanical pendulum that collides with an external moving mass is considered. The Melnikov function is derived to determine the effects of periodic collisions on the threshold condition for the appearance of Smale horseshoes chaos in the system. In order to counterbalance the action of the collision, a pulse-like periodic controller is used and the results show the efficiency of the controller to reduce the distortions due to collision and change the parameters boundary delineating the chaotic domain.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. M. di Bernardo, C. J. Budd, A. R. Champneys and P. Kowalczyk, Piecewise-smooth dynamical systems theory and applications, Springer-Verlag London Limited (2008).

    MATH  Google Scholar 

  2. W. Serweta, A. Okolewski, B. Blazejczyk-Okolewska, K. Czolczynski and T. Kapitaniak, Mirror hysteresis and Lyapunov exponents of impact oscillator with symmetrical soft stops, International Journal of Mechanical Sciences, 101-102 (2015) 89–98.

    Article  Google Scholar 

  3. F. Peterka, Behaviour of impact oscillator with soft and preloaded stop, Chaos, Solitons and Fractals, 18 (2003) 79–88.

    Article  Google Scholar 

  4. J. Newman and O. Makarenkov, Resonance oscillations in a mass-spring impact oscillator, Nonlinear Dyn, 79 (2015) 111–118.

    Article  MathSciNet  MATH  Google Scholar 

  5. S. L. T. de Souza, I. L. Caldas and R. L. Viana, Damping control law for a chaotic impact oscillator, Chaos, Solitons and Fractals, 32 (2007) 745–750.

    Article  Google Scholar 

  6. J. Lee, The corresponding phenomena of mechanical and electronic impact oscillator, Sound and Vibration, 311 (2008) 579–587.

    Article  Google Scholar 

  7. B. K. Clark, E. Rosa, A. D. Hall and T. R. Shepherd, Dynamics of an electronic impact oscillator, Physics Letters A, 318 (2003) 514–521.

    Article  Google Scholar 

  8. C. N. Bapat, Periodic motions of an impact oscillator, Sound and Vibration, 209 (2) (1998) 43–60.

    Article  Google Scholar 

  9. L. N. Virgin and C. J. Begley, Grazing bifurcations and basins of attraction in an impact-friction oscillator, Physica D, 130 (1999) 43–57.

    Article  MATH  Google Scholar 

  10. V. Sh. Burd and V. L. Krupenin, Subharmonic resonance oscillations of impact oscillator, Journal of Machinery Manufacture and Reliability, 40 (3) (2011) 201–207.

    Article  Google Scholar 

  11. H. Taghavifar, A. Mardani and A. H. Hosseinloo, Experimental analysis of the dissipated energy through tire-obstacle collision dynamics, Energy, 91 (2015) 573–578.

    Article  Google Scholar 

  12. C. Y. Xia, H. Xia and G. De Roeck, Dynamic response of a train-bridge system under collision loads and running safety evaluation of high-speed trains, Computers and Structures, 140 (2014) 23–38.

    Article  Google Scholar 

  13. Y. Yavin and C. Frangos, Control of a three-link manipulator: Collision avoidance of a moving obstacle, Computers and Mathematics with Applications, 47 (2004) 1627–1630.

    Article  MathSciNet  MATH  Google Scholar 

  14. A. Elmarakbi, M. Elkady and J. MacIntyre, Numerical analysis of vehicle-to-vehicle impact using vehicle dynamics control systems for collision mitigation, Int. J. Dynam. Control, 1 (2013) 172–191.

    Article  Google Scholar 

  15. H. Yuan and T. Shim, Model based real-time collision-free motion planning for nonholonomic mobile robots in unknown dynamic environments, Int. J. Precision Engineering and Manufacturing, 14 (3) (2013) 359–365.

    Article  Google Scholar 

  16. U. Benchetrit, E. Lenz and M. Shoham, Collision detection in static and dynamic complex scene not having geometric coherence, Int. J. Adv. Manuf. Technol., 14 (1998) 70–76.

    Article  Google Scholar 

  17. L. Ludwig and J. Haurykiewicz, Collision checking analysis tool: Discovering dynamic collisions in a modeling and simulation environment, Int. J. Interact. Des. Manuf., 1 (2007) 135–141.

    Article  Google Scholar 

  18. S. Yang and G. Chen, Study on dynamic simulation system for vessel’s collision process and its application, Procedia Engineering, 15 (2011) 3875–3880.

    Article  Google Scholar 

  19. H. Fang, J. Chen and L. Dou, Dynamic self-collision detection and prevention for 2-DOF robot arms using intervalbased analysis, Journal of Mechanical Science and Technology, 25 (8) (2011) 2077–2087.

    Article  Google Scholar 

  20. C. May, H. Janocha, E. Grasso and D. Naso, A pendulum actuator and its force generation capabilities, Proc. 7th Int. Conf. on Multibody Systems, Nonlinear Dynamics, and Control (2009) 1769–1775.

    Google Scholar 

  21. N. Ida, Design and control of a magnetic pendulum actuator, 13th Int. Conf. on Optimization of Electrical and Electronic Equipment (OPTIM) (2012) Doi: 10.1109/OPTIM. 2012.6231898.

    Google Scholar 

  22. Y. Guo and A. C. J Luo, Analytical bifurcation trees of a periodically excited pendulum, ASME Proc. Dynamics, Vibration and Control (2016) V04BT05A016, Doi: 10.1115/IMECE 2016-65916.

    Google Scholar 

  23. L. Zhou, S. S. Liu and F. Chen, Subharmonic bifurcations and chaotic motions for a class of inverted pendulum system, Chaos, Solitons and Fractals, 99 (2017) 270–277.

    Article  MathSciNet  MATH  Google Scholar 

  24. S. Li, X. Gong, W. Zhang and Y. Hao, The Melnikov method for detecting chaotic dynamics in a planar hybrid piecewise-smooth system with a switching manifold, Nonlinear Dynamics, 89 (2017) 939–953.

    Article  MathSciNet  Google Scholar 

  25. J. Xie, S.-H. He, Z.-H. Liu and Y. Chen, On application Melnikov method to detecting the edge of chaos for a microcantilever, New Advances in Mechanisms, Mechanical Transmission and Robotics (2016) 155–163.

    Google Scholar 

  26. M. Poliashenko and S. R. Mckay, Chaos due to homoclinic and heteroclinic orbits in two coupled oscillators with nonisochronism, Phys.Rev. A, 46 (1992) 5271–5274.

    Article  Google Scholar 

  27. J. C. Chedjou, P. Woafo and S. Domngang, Shilnikov chaos and dynamics of a self-sustained electromechanical transducer, J. Vibration and Acoustics, 123 (2001) 170–174.

    Article  Google Scholar 

  28. Y. Zhang, P. Shi, C.-C. Lim, H. Zhu, J. Hu and Y. Zeng, Chaotification of a class of linear switching systems based on Shilnikov criterion, J. Frankl. Inst., 354 (2017) 5519–5536.

    Article  MathSciNet  Google Scholar 

  29. Y. Zhang, P. Shi, H. Zhu, J. Hu and Y. Zeng, Generating chaos for a class of linear switching control systems: A hybrid approach, J. Frankl. Inst., 352 (2015) 5853–5865.

    Article  MathSciNet  Google Scholar 

  30. Y. Zhang, X. Liu, H. Zhu and Y. Zeng, Chaotification of a class of linear switching systems by hybrid driven methods, Int. J. Bifurc. Chaos, 24 (2014) 1450033.

    Article  MathSciNet  MATH  Google Scholar 

  31. A. Notué Kadjie and P. Woafo, Effects of springs on a pendulum electromechanical energy harvester, Theoretical & Applied Mechanics Letters, 4 (2014) 063001.

    Article  Google Scholar 

  32. V. K. Melnikov, On the stability of the center for time periodic perturbations, Trans. Moscow Math. SOC, 2 (1963) 1–57.

    Google Scholar 

  33. S. Wiggins, Introduction to applied nonlinear dynamical systems and chaos, Springer Verlag, New York (1990).

    Book  MATH  Google Scholar 

  34. H. Lee and J. Oh, Hopping system control with an approximated dynamics model and upper-body motion, Journal of Mechanical Science and Technology, 29 (11) (2015) 4891–4900.

    Article  Google Scholar 

  35. M. Nam, S. Han and J. Lee, Trajectory following control of mobile inverted pendulum robot with pre-determined tilt angle, Journal of Mechanical Science and Technology, 29 (12) (2015) 5417–5424.

    Article  Google Scholar 

  36. L.-W. Lee and I.-H. Li, Design and implementation of a robust FNN-based adaptive sliding-mode controller for pneumatic actuator systems, Journal of Mechanical Science and Technology, 30 (1) (2016) 381–396.

    Article  Google Scholar 

  37. J. Metsebo, N. Upadhyay, P. K. Kankar and B. R. Nana Nbendjo, Modelling of a rotor-ball bearings system using Timoshenko beam and effects of rotating shaft on their dynamics, Journal of Mechanical Science and Technology, 30 (12) (2016) 5339–5350.

    Article  Google Scholar 

  38. M. Ahmedalbashir, L. Romdhane and J. Lee, Dynamics of a four-bar mechanism with clearance and springs-Modeling and experimental analysis, Journal of Mechanical Science and Technology, 31 (3) (2017) 1023–1033.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratory of Modelling and Simulation in Engineering, Biomimetics and Prototypes, and TWAS Research Unit, Department of Physics, Faculty of Science, University of Yaoundé, I, P.O. Box 812, Yaoundé, Cameroon

    A. Notué Kadjie, I. Kemajou & P. Woafo

Authors
  1. A. Notué Kadjie
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. I. Kemajou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. P. Woafo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Notué Kadjie.

Additional information

Recommended by Associate Editor Hugo Rodrigue

Arnaud Notué Kadjie is a Ph.D. student at the University of Yaoundé 1, Cameroon. He is holder of a Master’s Degree in Physics obtained at the University of Yaoundè 1, Cameroon since 2012. His actual research is oriented towards the dynamics and control of electromechanical systems with the applications in the energy harvesting process and the optimization of actuator. He is a member of the research unit on Modeling and Simulation in Engineering and SPIE since 2015.

Isaac Kemajou was born on 16 October 1983 in Nkongsamba, Cameroon. He obtained his Master’s Degree in Physics at University of Yaoundé I. His research is concentrated on the dynamics of electromechanical systems having a strong nonlinear inductance at the research unit on Modeling and Simulation in Engineering, Biomimetics and Prototypes. He is a member of SPIE since 2015.

Paul Woafo is Professor of Physics at the University of Yaoundé I, Cameroon. He is holder of a “Doctorat de troisième cycle” and a “Doctorat d’Etat” both obtained in Cameroon in 1992 and 1997 in the field of Mechanics (Nonlinear Dynamics). He is presently managing a research unit on Modeling and Simulation in Engineering, Biomimetics and Prototypes (www.lamsebp.org) with strong interests in Electromechanical devices, control of vibrations, dynamics of semiconductor lasers, optoelectronic oscillators, chaos cryptography, biological physics, biomimetics, and appropriate technologies for development. His is presently co-author of more than 200 papers published in peer-reviewed journals by American Physical Society, American Institute of Physics, American Society of Mechanical Engineers, Elsevier-science, IOP-UK, Academic Press, Springer, IEEE, etc. He has been ICTP associate member from 1995 to 2005, and presently Senior Associate Member of ICTP, winner of the TWAS Prize for Young Scientists and Georg Forster Research fellow of the Humboldt Foundation (Germany). He has been to various institutions abroad for teaching and research.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Notué Kadjie, A., Kemajou, I. & Woafo, P. Control of an electromechanical pendulum subjected to impulsive disturbances using the Melnikov theory approach. J Mech Sci Technol 32, 865–874 (2018). https://doi.org/10.1007/s12206-018-0137-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-018-0137-x

Keywords

Search

Navigation