Skip to main content
SpringerLink
Log in

The self-excited vibrations of an axially retracting cantilever beam using the Galerkin method with fitted polynomial basis functions

  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

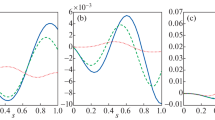
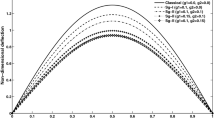
In the present study, the self-excited vibrations of an axially retracting beam under gravity is investigated. A GFB method is presented to discretize the system energy functions, in which the orthogonality relationships between the basis functions are needless. In this way, the motion equations can be derived in a much simpler way of matrix. The presented method and the derived motion equations are validated by comparing the computed results with which from previous literature. Based on the computed dynamic responses, the effect of gravity on beam dynamic behavior is investigated. An interesting phenomenon of self-excited vibration is observed as the beam retracts with a certain axial speed. Finally, the effects of retracting speed, structural damping and static tip deflection on self-excited vibration are investigated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. M. Stylianou and B. Tabarrok, Finite element analysis of an axially moving beam, Part I: Time integration, Journal of Sound and Vibration, 178 (4) (1994) 433–453.

    Article  Google Scholar 

  2. B. O. Al-Bedoor and Y. A. Khulief, Finite element dynamic modeling of a translating and rotating flexible link, Computer Methods in Applied Mechanics & Engineering, 131 (1–2) (1996) 173–189.

    Article  MATH  Google Scholar 

  3. B. O. Al-Bedoor and Y. A. Khulief, Vibrational motion of an elastic beam with prismatic and revolute joints, Journal of Sound and Vibration, 190 (2) (1996) 195–206.

    Article  Google Scholar 

  4. B. O. Al-Bedoor and Y. A. Khulief, General planar dynamics of a sliding flexible link, Journal of Sound & Vibration, 206 (5) (1997) 641–661.

    Article  Google Scholar 

  5. R. F. Fung, P. Y. Lu and C. C. Tseng, Non-linearly dynamic modelling of an axially moving beam with a tip mass, Journal of Sound and Vibration, 218 (4) (1998) 559–571.

    Article  Google Scholar 

  6. J. R. Chang et al., Vibration and stability of an axially moving Rayleigh beam, Applied Mathematical Modelling, 34 (6) (2010) 1482–1497.

    Article  MathSciNet  MATH  Google Scholar 

  7. S. Park, H. H. Yoo and J. Chung, Vibrations of an axially moving beam with deployment or retraction, Aiaa Journal, 51 (3) (2013) 686–696.

    Article  Google Scholar 

  8. S. Park, H. H. Yoo and J. Chung, Eulerian and Lagrangian descriptions for the vibration analysis of a deploying beam, Journal of Mechanical Science and Technology, 27 (9) (2013) 2637–2643.

    Article  Google Scholar 

  9. B. Kim and J. Chung, Residual vibration reduction of a flexible beam deploying from a translating hub, Journal of Sound and Vibration, 333 (16) (2014) 3759–3775.

    Article  Google Scholar 

  10. S. Park and J. T. Chung, Dynamic analysis of an axially moving finite-length beam with intermediate spring supports, Journal of Sound and Vibration, 333 (24) (2014) 6742–6759.

    Article  Google Scholar 

  11. K. Zhu and J. Chung, Nonlinear lateral vibrations of a deploying Euler–Bernoulli beam with a spinning motion, International Journal of Mechanical Sciences, 90 (2015) 200–212.

    Article  Google Scholar 

  12. Y. Huo and Z. Wang, Dynamic analysis of a vertically deploying/retracting cantilevered pipe conveying fluid, Journal of Sound and Vibration, 360 (2016) 224–238.

    Article  Google Scholar 

  13. Y. C. Duan et al., Theoretical and experimental study on the transverse vibration properties of an axially moving nested cantilever beam, Journal of Sound and Vibration, 333 (13) (2014) 2885–2897.

    Article  Google Scholar 

  14. L. Ning and Y. Guolai, Vibration property analysis of axially moving cantilever beam considering the effect of moving mass, Journal of Vibration and Shock, 31 (3) (2012) 102–105.

    Google Scholar 

  15. Y. Matsuzaki, Y. Taki and M. Toyama, Vibration of a cantilevered beam during deployment and retrieval: Analysis and experiment, Smart Materials & Structures, 4 (4) (1998) 334–339 (336).

    Article  Google Scholar 

  16. B. O. Al-Bedoor and Y. A. Khulief, An approximate analytical solution of beam vibrations during axial motion, Journal of Sound and Vibration, 192 (1) (1996) 159–171.

    Article  Google Scholar 

  17. H. Shin and S. Rhim, Modeling and control of lateral vibration of an axially translating flexible link, Journal of Mechanical Science and Technology, 29 (1) (2015) 191–198.

    Article  Google Scholar 

  18. H. Zhang and L. Chen, Vibration of an axially moving string supported by a viscoelastic foundation, Acta Mechanica Solida Sinica, 29 (3) (2016) 221–231.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing, 210094, China

    Hongliang Hua, Zhenqiang Liao & Xiangyan Zhang

Authors
  1. Hongliang Hua
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhenqiang Liao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xiangyan Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hongliang Hua.

Additional information

Recommended by Associate Editor Eung-Soo Shin

Hongliang Hua is a doctoral student at Nanjing University of Science and Technology in Nanjing, China. His current research interests include nonlinear dynamics, structural optimization, time-varying Finite element method and rigid-flexible coupled dynamics.

Zhenqiang Liao received his Ph.D. degree in Engineering from Nanjing University of Science and Technology in Nanjing, China. He is a Professor at Department of Mechanical Design, School of Mechanical Engineering, Nanjing University of Science and Technology. His main subjects are multi-body dynamics, vibration reduction for machine gun system and weapon structural optimization.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hua, H., Liao, Z. & Zhang, X. The self-excited vibrations of an axially retracting cantilever beam using the Galerkin method with fitted polynomial basis functions. J Mech Sci Technol 32, 29–36 (2018). https://doi.org/10.1007/s12206-017-1204-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-017-1204-z

Keywords

Search

Navigation