Skip to main content
SpringerLink
Log in

On the characteristics of an ultra-low frequency nonlinear isolator using sliding beam as negative stiffness

  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

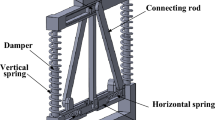
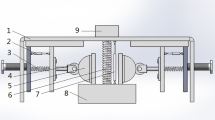
A novel structured ultra-low frequency nonlinear passive isolator is presented. The isolator is composed of a knife-edge supported sliding beam which offers negative stiffness and a vertical mechanical spring in parallel to get quasi-zero dynamic stiffness. The static characteristics of the isolator are studied. Assuming light viscous damping, the dynamic behavior is investigated and the response under harmonic excitation is derived using a simple approximation. Frequency response curves (FRCs), which exhibit complex double jump phenomenon, are obtained by harmonic balance method (HBM). The limitation of the excitation force level is obtained. The force transmissibility is derived and compared with an equivalent linear system with the same damping ratio. The isolation performance of the nonlinear isolator is shown to outperform the linear system for providing a wider isolation region. The influence of system parameters on the transmissibility is examined and some useful guidelines are given.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. C. M. Harris and A. G. Piersol, Shock and vibration handbook, 5th ed. McGraw-Hill, New York, USA (2002).

    Google Scholar 

  2. W. G. Molynewx, Supports for vibration isolation, Ministry of Supply, Tech. Note No.: Structures 211, United Kingdom (1956).

    Google Scholar 

  3. P. Alabuzhev, A. Gritchin, L. Kim, G. Migirenko, V. Chon and P. Stepanov, Vibration protecting and measuring systems with quasi-zero stiffness, Hemisphere Publishing, New York, USA (1989).

    Google Scholar 

  4. R. A. Ibrahim, Recent advances in nonlinear passive vibration isolators, J. Sound Vib., 314 (2008) 371–452.

    Article  Google Scholar 

  5. L. N. Virgin and R. B. Davis, Vibration isolation using buckled struts, J. Sound Vib., 260 (2003) 965–973.

    Article  Google Scholar 

  6. L. N. Virgin, S. T. Santillan and R. H. Plaut, Vibration isolation using extreme geometric nonlinearity, J. Sound Vib., 315 (2008) 721–731.

    Article  Google Scholar 

  7. D. L. Platus, Negative-stiffness-mechanism vibration isolation systems, Proc. of SPIE-The International Society for Optical Engineering, Vibration Control in Microelectronics, Optics and Metrology, San Jose, CA, USA (1992) 44–54.

    Chapter  Google Scholar 

  8. H. J. Ahn, Performance limit of a passive vertical isolator using a negative stiffness mechanism, J. Mech. Sci. Technol., 22 (2008) 2357–2364.

    Article  Google Scholar 

  9. A. Carrella, M. J. Brennan and T. P. Waters, Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic, J. Sound Vib., 301 (2007) 678–689.

    Article  Google Scholar 

  10. A. Carrella, Passive Vibration isolators with high-staticlow-dynamic-stiffness, Ph.D. Thesis, ISVR, University of Southampton, United Kingdom (2008).

    Google Scholar 

  11. I. Kovacic, M. J. Brennan and T. P. Waters, A study of a nonlinear vibration isolator with a quasi-zero stiffness characteristic, J. Sound Vib., 315 (2008) 700–711.

    Article  Google Scholar 

  12. N. Zhou, K. Liu, A tunable high-static-low-dynamic stiffness vibration isolator, J. Sound Vib., 329 (2010) 1254–1273.

    Article  Google Scholar 

  13. A. Carrella, M. J. Brennan, T. P. Waters and K. Shin, On the design of a high-static-low-dynamic stiffness isolator using linear mechanical springs and magnets, J. Sound Vib., 315 (2008) 712–720.

    Article  Google Scholar 

  14. T. Mizuno, T. Toumiya and M. Takasaki, Vibration isolation system using negative stiffness, JSME Int. J., Ser. C, 46 (2003) 807–812.

    Article  Google Scholar 

  15. R. Somnay, R. A. Ibrahim and R. C. Banasik, Nonlinear dynamics of a sliding beam on two supports and its efficacy as a non-traditional isolator, J. Vib. Control, 12 (2006) 685–712.

    Article  MATH  Google Scholar 

  16. A. H. Nayfeh and D. T. Mook, Nonlinear oscillations, Wiley, New York, USA (1979).

    MATH  Google Scholar 

  17. C. Hayashi, Nonlinear oscillations in physical systems, McGraw-Hill, New York, USA (1964).

    MATH  Google Scholar 

  18. W. Szemplinska-Stupnicka and J. Bajkowski, The \({\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}\) subharmonic resonance and its transition to chaotic motion in a non-linear oscillator, Int. J. Non Linear Mech., 21 (1986) 401–419.

    Article  MATH  MathSciNet  Google Scholar 

  19. B. Ravindra and A. K. Mallik, Performance of non-linear vibration isolators under harmonic excitation, J. Sound Vib., 170(3) (1994) 325–337.

    Article  MATH  Google Scholar 

  20. I. Kovacic, M. J. Brennan and B. Lineton, On the resonance response of an asymmetric Duffing oscillator, Int. J. Non Linear Mech., 43(9) (2008) 858–867.

    Article  Google Scholar 

  21. I. Kovacic, M. J. Brennan and B. Lineton, Effect of a static force on the dynamic behaviour of a harmonically excited quasi-zero stiffness system, J. Sound Vib., 325 (2009) 870–883.

    Article  Google Scholar 

  22. R. A. Ibrahim and R. J. Somnay, Nonlinear dynamic analysis of an elastic beam isolator sliding on frictional supports, J. Sound Vib., 308 (2007) 735–757.

    Article  Google Scholar 

  23. F. Benedettini and G. Rega, Non-linear dynamics of an elastic cable under planar excitation, Int. J. Non Linear Mech., 22(6) (1987) 497–509.

    Article  MATH  Google Scholar 

  24. Z. Rahman and T. D. Burton, Application of catastrophe theory to forced vibration of a diaphragm air spring, J. Sound Vib., 110 (1986) 363–380.

    Article  MATH  MathSciNet  Google Scholar 

  25. M. Bayat, M. Shahidi1, A. Barari and G. Domairry, The approximate analysis of nonlinear behavior of structure under harmonic loading, Int. J. Phys. Sci., 5(7) (2010) 1074–1080.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Vibration, Shock & Noise, Shanghai Jiao Tong University, Shanghai, 200240, China

    Xiuchang Huang, Xintian Liu & Hongxing Hua

  2. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University, Shanghai, 200240, China

    Hongxing Hua

Authors
  1. Xiuchang Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xintian Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hongxing Hua
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Xiuchang Huang or Hongxing Hua.

Additional information

Recommended by Associate Editor Ohseop Song

X. Ch. Huang received his Ph.D. from the School of Mechanical Engineering at Shanghai Jiao Tong University. He is now a lecturer at the School of Mechanical Engineering. His research interests include vibration analysis and control.

X. T. Liu received his Ph.D. from the School of Mechanical Engineering at Shanghai Jiao Tong University. He is now an engineer at China Aerospace Science and Technology Corporation. His research interests include vibration analysis and control.

H. X. Hua received his Ph.D. from the University of Brussels in Belgium. He is a Professor and Doctoral Supervisor at the School of Mechanical Engineering. His research interests include vibration and shock analysis; vibration and shock control.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Huang, X., Liu, X. & Hua, H. On the characteristics of an ultra-low frequency nonlinear isolator using sliding beam as negative stiffness. J Mech Sci Technol 28, 813–822 (2014). https://doi.org/10.1007/s12206-013-1205-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-013-1205-5

Keywords

Search

Navigation