Skip to main content
SpringerLink
Log in

Buckling analysis of circular and annular composite plates reinforced with carbon nanotubes using FEM

  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

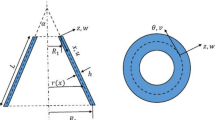
The critical compressive load in the buckling of circular and annular composite plates reinforced with carbon nanotubes (CNTs) is calculated using finite element method. The developed model is based on the third-order shear deformation theory for moderately thick laminated plates. Effects of CNTs orientation angles and thickness-to-inner radius ratio on the buckling of composite plates are discussed. The results are compared with those obtained by analytical method based on classical plate theory. The finite element method shows lower values for critical buckling load because of the elimination of shear strain in the classical plate theory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. B. Hornbostela, P. Po. Tschkeb, J. Kotza and S. Roth, Mechanical properties of triple composites of polycarbonate, single-walled carbon nanotubes and carbon fibres, Physica E: Low Dimensional Systems and Nanostructures, 40(7) (2008) 2434–2439.

    Article  Google Scholar 

  2. A. L. Kalamkarov, A. V. Georgiades, S. K. Rokkam, V. P. Veedu and M. N. Ghasemi Nejhad, Analytical and numerical techniques to predict carbon nanotubes properties, International Journal of Solids and Structures, 43(22) (2006) 6832–6854.

    Article  MATH  Google Scholar 

  3. M. K. Amal, M. Farag and M. Mahmoud, Carbon nanotube reinforced composites: potential and current challenges, Material design, 28(9) (2007) 2394–2401.

    Article  Google Scholar 

  4. H. Wan, F. Delale and L. Shen, Effect of CNT length and CNT-matrix interphase in carbon nanotube (CNT) reinforced composites, Mechanics Research Communications, 32(5) (2005) 481–489.

    Article  MATH  Google Scholar 

  5. L. S. Ma and T. J. Wang, Relationships between axisymmetric bending and buckling solutions of FGM circular plates based on third-order plate theory and classical plate theory, International Journal of Solids and Structures, 41(1) (2004) 85–101.

    Article  MATH  Google Scholar 

  6. M. M. Najafizadeh and H. R. Heydari, An exact solution for buckling of functionally graded circular plates based on higher order shear deformation plate theory under uniform radial compression, International Journal of Mechanical Science, 50(3) (2007) 603–612.

    Article  Google Scholar 

  7. B. Bremec and F. Kosel, Thickness optimization of circular annular plate at buckling, Thin Walled Structures, 44(1) (2006) 74–81.

    Article  Google Scholar 

  8. A. R. Saidi, A. Rasouli and S. Sahraee, Axisymmetric bending and buckling analysis of thick functionally graded circular plates using unconstrained third-order shear deformation plate theory, Composite Structures, 89(1) (2009) 110–119.

    Article  Google Scholar 

  9. H. Tan, Y. Huang, C. Liu and P. H. Geubelle, The Mori Tanaka method for composite materials with nonlinear interface debonding, International Journal of Plasticity, 21(10) (2005) 1890–1918.

    Article  MATH  Google Scholar 

  10. L. P. Kollar and G. S. Springer, Mechanics of composite structures, Cambridge University, NY, USA (2003).

    Book  Google Scholar 

  11. D. L. Shi, X. Q. Feng, Y. Y. Huang, K. C. Hwang and H. Gao, The effect of nanotube waviness and agglomeration on the elastic property of carbon nanotube reinforced composites, Department of Engineering Mechanics, 126(3) (2004) 250–258.

    Google Scholar 

  12. V. N. Popov, V. E. Van Dorena and M. Balkanskib, Elastic properties of crystals of single-walled carbon nanotubes, Solid State Communications, 114(7) (2000) 395–399.

    Article  Google Scholar 

  13. J. R. Vinson, The behavior of thin walled structures, beams, plates and shells, Kluwer Academic (1989).

  14. P. Singhatanadgid and V. Ungbhakorn, Scaling laws for buckling of polar orthotropic annular plates subjected to compressive and torsional loading, Thin Walled Structures, 43(7) (2005) 1115–1129.

    Article  Google Scholar 

  15. J. N. Reddy, An introduction to the finite element method, McGraw-Hill (1993).

Download references

Author information

Authors and Affiliations

  1. Composite Materials and Technology Center, Tehran, Iran

    Sh. Maghamikia & J. E. Jam

Authors
  1. Sh. Maghamikia
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. E. Jam
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to J. E. Jam.

Additional information

This paper was recommended for publication in revised form by Editor Maenghyo Cho

Sh. Maghamikia received his B.S degree from Islamic Azad University in Tehran, Iran, in 2007. He received his M.S degree from University of Kashan in Kashan, Iran, in 2009. His research interests include nanomechanics, functionally graded materials (FGMs) and finite element method (FEM).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Maghamikia, S., Jam, J.E. Buckling analysis of circular and annular composite plates reinforced with carbon nanotubes using FEM. J Mech Sci Technol 25, 2805–2810 (2011). https://doi.org/10.1007/s12206-011-0738-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-011-0738-8

Keywords

Search

Navigation