Skip to main content
SpringerLink
Log in

Bearing fault diagnosis based on amplitude and phase map of Hermitian wavelet transform

  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

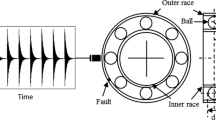
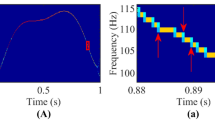
The rolling element bearing characteristic frequencies contain very little energy and are usually overwhelmed by noise and higher level of structural vibrations. The continuous wavelet transform enables one to look at the evolution in the time scale joint representation plane. This makes it very suitable for the detection of singularity generated by localized defects in a mechanical system. However, most applications of the continuous wavelet transform have widely focused on the use of the Morlet wavelet transform. The complex Hermitian wavelet is constructed based on the first and the second derivatives of the Gaussian function to detect signal singularities. The Fourier spectrum of Hermitian wavelet is real, which the Fourier spectrum has no complex phase and the Hermitian wavelet does not affect the phase of a signal in complex domain. This gives the desirable ability to detect the singularity characteristic of a signal precisely. In this study, the Hermitian wavelet amplitude and phase map are used in conjunction to detect and diagnose the bearing fault. The Hermitian wavelet amplitude and phase map are found to show distinctive signatures in the presence of bearing inner race or outer race damage. The simulative and experimental results show that the Hermitian wavelet amplitude and phase map can extract the transients from strong noise signals and can effectively diagnose bearing faults.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. N. Tandon and A. Choudhury, An analytical model for the prediction of the vibration response of rolling element bearings due to a localized defect, Journal of Sound and Vibration, 205(3) (1997) 275–292.

    Article  Google Scholar 

  2. P. D. McFadden and J. D. Smith, Model for the vibration produced by a single point defect in a rolling element bearing, Journal of Sound and Vibration, 96(1) (1984) 69–82.

    Article  Google Scholar 

  3. J. Lin and L. Qu, Feature extraction based on Morlet wavelet and its application for mechanical fault diagnosis, Journal of Sound and Vibration, 234(1) (2000) 135–148.

    Article  Google Scholar 

  4. P. D. McFadden and J. D. Smith, Vibration monitoring of rolling element bearings by the high-frequency resonance technique—a review, Tribology International, 17(1) (1984) 3–10.

    Article  Google Scholar 

  5. D. Ho and R. B. Randall, Optimization of bearing diagnostic techniques using simulated and actual bearing fault signals, Mechanical Systems and Signal Processing, 14(5) (2000) 763–788.

    Article  Google Scholar 

  6. P. Maragos, J. F. Kaiser, and T. F. Quatieri, On amplitude and frequency demodulation using energy operators, IEEE Transactions on Signal Processing, 41(5) (1993) 1532–1550.

    Article  MATH  Google Scholar 

  7. H. Li and H. Zheng, Bearing Fault Detection Using Envelope Spectrum Based on EMD and TKEO, Proceedings of the 5th International Conference on Fuzzy Systems and Knowledge Discovery, 3 (2008) 142–146.

    Article  Google Scholar 

  8. L. Cohen, Time-frequency analysis, Prentice-Hall, Englewood Cliffs, NJ, 1995.

    Google Scholar 

  9. Q. Meng and L. Qu, Rotating machinery fault diagnosis using Wigner distribution, Mechanical Systems and Signal Processing, 5(3) (1991) 155–166.

    Article  Google Scholar 

  10. W. J. Staszewski, K. Worden and G. R. Tomlinson, Thefrequency analysis in gearbox fault detection using the Wigner-Ville distribution and pattern recognition, Mechanical Systems and Signal Processing, 11(5) (1997) 673–692.

    Article  Google Scholar 

  11. W. J. Staszewski, Wavelet based compression and feature selection for vibration analysis, Journal of Sound and Vibration, 211(5) (2000) 736–760.

    Google Scholar 

  12. C. J. Li and J. Ma, Wavelet decomposition of vibration for detection of bearing-localized defects, NDT&E International, 30(3) (1997) 143–149.

    Article  MathSciNet  Google Scholar 

  13. S. Prabhakar, A. R. Mohanty and A. S. Sekhar, Application of discrete wavelet transform for detection of ball bearing race fault, Tribology International, 3(12) (2002) 793–800.

    Article  Google Scholar 

  14. H. Li, Y. Zhang and H. Zheng, Hilbert-Huang transform and marginal spectrum for detection and diagnosis of localized defects in roller bearings, Journal of Mechanical Science and Technology, 23(2) (2009) 291–301.

    Article  MathSciNet  Google Scholar 

  15. R. Rubini and U. Meneghetti, Application of the envelope and wavelet transform analyses for the diagnosis of incipient faults in ball bearings, Mechanical Systems and Signal Processing, 15(2) (2001) 287–302.

    Article  Google Scholar 

  16. N. G. Nikolaou and I. A. Antoniadis, Demodulation of vibration signals generated by defects in rolling element bearings using complex shifted Morlet wavelets, Mechanical Systems and Signal Processing, 16(4) (2002) 677–694.

    Article  Google Scholar 

  17. C. Junsheng, Y. Dejie, and Y. Yu, Application of an impulse response wavelet to fault diagnosis of rolling bearings, Mechanical Systems and Signal Processing, 21(2) (2007) 920–929.

    Article  Google Scholar 

  18. W. J. Wang, Wavelets for detecting mechanical faults with high sensitivity, Mechanical Systems and Signal Processing, 15(4) (2001) 685–696.

    Article  Google Scholar 

  19. J. Lin and M. J. Zuo, Gearbox fault diagnosis using adaptive wavelet filter, Mechanical Systems and Signal Processing, 17(6) (2003) 1259–1269.

    Article  Google Scholar 

  20. D. Moulahbal, M. F. Golnaraghi and F. Ismail, Amplitude and phase wavelet maps for the detection of cracks in geared systems, Mechanical Systems and Signal Processing, 13(3) (1999) 423–436.

    Article  Google Scholar 

  21. W. J. Wang and P. D. McFadden, Application of orthogonal wavelets to early gear damage detection, Mechanical Systems and Signal Processing, 9(5) (1995) 497–507.

    Article  Google Scholar 

  22. W. J. Wang and P. D. McFadden, Application of wavelets to gearbox vibration signals for fault detection, Journal of Sound and Vibration, 192(5) (1996) 927–939.

    Article  Google Scholar 

  23. H. Ssu, C. Hsu, L. D. Sa and W. Li, Hermitian Hat wavelet design for singularity detection in the PARAGUAY river level data analysis, Proceeding of SPIE The International Socity for Optical Engineering, 3078 (1997) 96–115.

    Google Scholar 

  24. Z. He, Y. Zi, Q. Meng and et al., Fault diagnosis principle of non-stationary signal and application to mechanical equipment, Higher Education Press, 2001.

  25. H. Li, Y. Zhang and H. Zheng, Application of Hermitian wavelet to crack fault detection in gearbox, Mechanical Systems and Signal Processing, 25(4) (2011) 1353–1363.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electromechanical Engineering, Shijiazhuang Institute of Railway Technology, Shijiazhuang, 050041, China

    Hui Li & Lihui Fu

  2. First Department, Shijiazhuang Mechanical Engineering College, Shijiazhuang, 050003, China

    Haiqi Zheng

Authors
  1. Hui Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lihui Fu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Haiqi Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hui Li.

Additional information

This paper was recommended for publication in revised form by Associate Editor Eung-Soo Shin

Hui Li received his B.S. in Mechanical Engineering from Hebei Polytechnic University, Hebei, China, in 1991. He received his M.S. in Mechanical Engineering from Harbin University of Science and Technology, Heilongjiang, China, in 1994, and his Ph.D from Tianjin University’s School of Mechanical Engineering, Tianjin, China, in 2003. He was a postdoctoral researcher at Shijiazhuang Mechanical Engineering College from August 2003 to September 2005, and at Beijing Jiaotong University from March 2006 to December 2008. He is currently a professor of Mechanical Engineering at Shijiazhuang Institute of Railway Technology, China. His research and teaching interests include hybrid drive mechanisms, kinematics and dynamics of machinery, mechatronics, CAD/CAPP, and signal processing for machine health monitoring, diagnosis and prognosis. He is currently a senior member of the Chinese Society of Mechanical Engineering.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Li, H., Fu, L. & Zheng, H. Bearing fault diagnosis based on amplitude and phase map of Hermitian wavelet transform. J Mech Sci Technol 25, 2731–2740 (2011). https://doi.org/10.1007/s12206-011-0717-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-011-0717-0

Keywords

Search

Navigation