Abstract
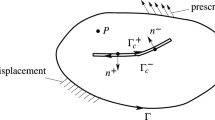
In this work, element free Galerkin method (EFGM) has been used to obtain the solution of various edge crack problems under thermo-mechanical loads as it provides a versatile technique to model stationary as well as moving crack problems without re-meshing. Standard diffraction criterion has been modified with multiple crack weight technique to characterize the presence of various cracks in the domain of influence of a particular node. The effect of crack inclination has been studied for single as well as two edge cracks, whereas the cracks interaction has been studied for two edge cracks lying on same as well as opposite edges under plane stress conditions. The values of mode-I and mode-II stress intensity factors have been evaluated by the interaction integral approach.
Similar content being viewed by others
References
J. Lansinger, T. Hansson and O. Clevfors, Fatigue crack growth under combined thermal cycling and mechanical loading, International Journal of Fatigue, 29 (2007) 1383–1390.
B. Muravin and E. Turkel, Multiple crack weight for solution of multiple interacting cracks by meshless numerical methods, International Journal for Numerical Methods in Engineering, 67 (2006) 1146–1159.
K. Y Dai, G. R Liu, X. Han, and K. M. Lim, Thermomechanical analysis of functionally graded material (FGM) plates using element-free Galerkin method, Computers and Structures, 83 (2005) 1487–1502.
T. Belytschko and S. Loehnert, Crack shielding and amplification due to multiple micro-cracks interacting with a macrocrack, International Journal of Fracture, 145 (2007) 1–8.
T. Belytschko and Y. Lu, Element-free Galerkin methods, International Journal for Numerical Methods in Engineering, 37 (1994) 229–256.
B. Muravin, The Application of Element Free Galerkin Method in the Investigation of Crack Interaction, Ph.D. Thesis, Tel-Aviv University, Israel (2003).
T. Belytschko and M. Fleming, Smoothing, enrichment and contact in the element-free Galerkin method, Computers and Structures, 71 (1999) 173–195.
D. J. Organ, M. Fleming and T. Belytschko, Continuous meshless approximation for non-convex bodies by diffraction and transparency, Computational Mechanics, 18 (1996) 225–235.
Y. Krongauz and T. Belytschko, Enforcement of essential boundary conditions in meshless approximations using Finite Elements, Computer Methods in Applied Mechanics and Engineering, 131 (1996) 133–145.
P. Nguyen, T. Rabczuk, S. Bordas and M. Duflot, Meshless methods: A review and computer implementation aspects, Mathematics and Computers in Simulation, 79 (2008) 763–813.
P. Beer, E. Johnston and T. DeWolf, Mechanics of Materials, McGraw-Hill International Edition (2002).
J. Dolbow and T. Belytschko, Numerical integration of Galerkin weak form in Meshfree methods, Computational Mechanics, 23 (1999) 219–230.
S. Dag, Thermal fracture analysis of orthotropic functionally graded materials using an equivalent domain integral approach, Engineering Fracture Mechanics, 73(2006)2802–2828.
J. Dolbow and T. Belytschko, An introduction to programming the meshless element free Galerkin method, Archives of Computational Methods in Engineering, 5 (1998) 207–241.
T. L. Anderson, Fracture Mechanics Fundamentals and Applications, Taylor and Francis (2005).
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper was recommended for publication in revised form by Associate Editor Seong Beom Lee
Mohit Pant received his B. Tech. in Mechanical Engineering from Uttar Pradesh Technical University, Lucknow, India in 2004. He received his M. Tech in Design & Production Engineering from Govind Ballab Pant University of Agriculture and Technology, Pantnagar, India in 2006 and his PhD from Indian Institute of Technology, Roorkee, India in 2010. His research interests include computational fracture mechanics and meshfree methods.
Indra Vir Singh is working as an Assistant Professor in the Department of Mechanical and Industrial Engineering, Indian Institute of Technology Roorkee, India since 2007. He received his B.Tech. Degree in Mechanical from AMU Aligarh, India in 1996, M.Tech. in Applied Mechanics from IIT Delhi, India in 1998, and Ph.D. in Meshfree Methods from BITS Pilani, India in 2004. He has more than 10 years of Teaching and Research Experience. He has more than 80 research articles in various Journals and Conferences. His research interests include FEM, XFEM, Meshfree Methods, Elasto-Plastic Simulations, Fracture and Fatigue.
B. K. Mishra is presently working as a Professor in the Department of Mechanical and Industrial Engineering, Indian Institute of Technology Roorkee, India. He received his B.Tech. Degree in Mechanical Engg. from BHU Vanarasi, India in 1982, M.Tech. in Mechanical Engg. from IIT Kanpur, India in 1985, and Ph.D. in Mechanical Engg. from BHU Varanasi, India in 1990. He has more than 20 years of Teaching and Research Experience. He has about 100 research articles in various Journals and Conferences. His research interests include FEM, XFEM, Fracture, Fatigue and Vibrations.
Rights and permissions
About this article
Cite this article
Pant, M., Singh, I.V. & Mishra, B.K. A numerical study of crack interactions under thermo-mechanical load using EFGM. J Mech Sci Technol 25, 403–413 (2011). https://doi.org/10.1007/s12206-010-1217-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12206-010-1217-3