Skip to main content
SpringerLink
Log in

Reduced order model of three-dimensional Euler equations using proper orthogonal decomposition basis

  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

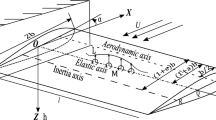
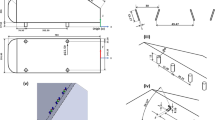
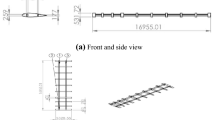
This study seeks to validate the accuracy and the efficiency of the aerodynamic reduced order model (ROM). In doing this, snapshot data are generated from the full system analysis of a fighter wing problem. From an eigensystem analysis of these snapshots, the basis vector reproducing the behavior of the full system is obtained. The span length, sweep angle, dihedral angle, and spar and rib thickness representing the wing configuration are determined as the input variables. The constructed ROM is applied to the fighter wing problem while varying the input conditions for validation. Subsequently, a comparison of the reduced system with the full system confirmed that the aerodynamic performance is within 4% error and that the L2 norms are 10−6 order of the entire flow field. Therefore, the ROM is able to capture the variation of the aerodynamic performance with respect to the input variables. Though there are structural input variables which influence the aerodynamic performance indirectly, the ROM can reproduce the flow field of the full system. Additionally, even if the ROM incurs a high computational cost to generate snapshots, it can represent the behavior of the full system efficiently once the reduced order model is constructed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. D. J. Lucia, P. S. Beran and W. A. Silva, Reduced-order modeling: new approaches for computational physics, Aerospace Science, 40 (2004) 51–117.

    Article  Google Scholar 

  2. D. J. Lucia, Reduced Order Modelling for High Speed Flows With Moving Shocks, Ph. D Thesis, Air Force Institute of Technology, School of Engineering and Management, (2001).

  3. P. Holmes, J. L. Lumley and G. Berkooz, Turbulence, Coherent Structures, Dynamical Systems and Symmetry, Cambridge University Press, Cambridge, UK, (1996).

    Google Scholar 

  4. Taehyoun Kim, Efficient Reduced-Order System Identification for Linear Systems with Multiple Inputs, AIAA journal, 43(7) (2005) 1455–1464.

    Article  Google Scholar 

  5. P. S. Beran, D. J. Lucia and C. L. Pettit, Reduced-Order Modelling of Limit-Cycle Oscillation for Aeroelastic Systems, Journal of Fluids and Structures, 19 (2004) 575–590.

    Article  Google Scholar 

  6. G. A. Ashford, An Unstructured Grid Generation and Adaptive Solution Technique for High-Reynolds-Number Compressible Flows, Ph. D thesis, University of Michigan, (1996).

  7. D. L. Whitaker, Two-dimensional Euler Computations on a Triangular Mesh Using an Upwind, Finite-Volume Scheme, Ph. D thesis, Virginia Polytechnic Institute and State University, (1988).

  8. W. K. Anderson and D. L. Bonhaus, An Implicit Upwind Algorithm for Computing Turbulent Flows on Unstructured Grids, Computer Fluids, 23(1) (1994) 1–21.

    Article  MATH  Google Scholar 

  9. V. Venkatakrishnan, Convergence to Steady Solutions of the Euler Equations on Unstructured Grids with Limiters, Journal of computational physics, 118 (1995) 120–130.

    Article  MATH  Google Scholar 

  10. V. Schmitt and F. Charpin, Pressure Distributions on the ONERA-M6-Wing at Transonic Mach Numbers, Experimental Data Base for Computer Program Assessment. Report of the Fluid Dynamics Panel Working Group 04, AGARD AR 138, May 1979.

  11. M. A. Aminpour, An assumed stress hybrid 4 node shell element with drilling degrees of freedom, International Journal for Numerical Methods in Engineering, 33 (1992) 11–38.

    Article  Google Scholar 

  12. Maenghyo Cho and Hyungi Kim, A refined semi-analytic design sensitivity based the mode decomposition and Neumann series, International Journal for Numerical Methods in Engineering, 62 (2005) 19–49.

    Article  MATH  Google Scholar 

  13. D. S Choi, J. O. Jun, B. K. Kim, S. H. Park, M. H. Cho, D. H. Lee, K. T. Lee and S. M. Jun, Static Aeroelastic Analysis for Aircraft Wings using CFD/CST Coupling Methodology, Journal of the Korea Society for Aeronautical and Space Sciences, 35(4) (2007) 287–294.

    Google Scholar 

  14. M. K. Bhardwaj, A CFD/CSD Interaction Methodology for Aircraft Wings, Ph.D. thesis, Department of Aerospace Engineering, The Virginia State University at Blacksburg, Virginia, (1997).

    Google Scholar 

  15. J. T. Batina, Unsteady Euler Airfoil Solutions Using Unstructured Dynamic Meshes, AIAA Journal, 28(8) (1990) 1381~1388.

    Article  Google Scholar 

  16. B. K. Kim, S. O. Jun, Y. H. Jeon, J. H. Kim and D. H. Lee, Efficiency of Dynamic Mesh in Static Aeroelastic Analysis and Design Optimization Problem, Journal of the Korea Society for Aeronautical and Space Sciences, 35(2) (2007) 87–93.

    Article  Google Scholar 

  17. Y. S. Kim, J. Kim, Y. H. Jeon, J. S. Bang, D. H. Lee, Y. H. Kim and C. Park, Multidisciplinary Aerodynamic-Structural Design Optimization of Supersonic Fighter Wing Using Response Surface Methodology, 40 th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, USA, (2002) AIAA-2002-0322.

Download references

Author information

Authors and Affiliations

  1. School of Mechanical and Aerospace Engineering, Seoul National University, Seoul, 151-742, Korea

    Sangook Jun, Kyung-Hyun Park, Hyung-Min Kang & Maenghyo Cho

  2. School of Mechanical and Aerospace Engineering/Institute of Advanced Aerospace Technology, Seoul National University, Seoul, 151-742, Korea

    Dong-Ho Lee

Authors
  1. Sangook Jun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kyung-Hyun Park
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hyung-Min Kang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Dong-Ho Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Maenghyo Cho
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dong-Ho Lee.

Additional information

This paper was recommended for publication in revised form by Associate Editor Do Hyung Lee

Sangook Jun is a Ph.D candidate, in the integrated MA/Ph.D Course at Seoul National University. His B.S degree is from Seoul National University. The research topic of interest is a robust design optimization and a reduced order model.

Dongho Lee is a professor at Seoul National University. A member of The National Academy of Engineering of Korea, he is also the director of Institute of Advanced Aerospace Technology, Seoul National University. He is interested in Computational Fluid Dynamics, wind tunnel test and Multidisciplinary Design Optimization for large and complex systems (e.g. aircraft, helicopter, high speed train, compressor and wind turbine).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jun, S., Park, KH., Kang, HM. et al. Reduced order model of three-dimensional Euler equations using proper orthogonal decomposition basis. J Mech Sci Technol 24, 601–608 (2010). https://doi.org/10.1007/s12206-010-0106-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-010-0106-0

Keywords

Search

Navigation