Skip to main content
SpringerLink
Log in

Free vibration analysis of functionally graded coupled circular plate with piezoelectric layers

  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

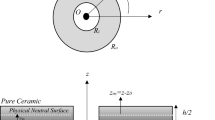
Based on classical plate theory (CLPT), free vibration analysis of a circular plate composed of functionally graded material (FGM) with its upper and lower surfaces bounded by two piezoelectric layers was performed. Assuming that the material properties vary in a power law manner within the thickness of the plate the governing differential equations are derived. The distribution of electric potential along the thickness direction in piezoelectric layers is considered to vary quadratically such that the Maxwell static electricity equation is satisfied. Then these equations are solved analytically for two different boundary conditions, namely clamped and simply supported edges. The validity of our analytical solution was checked by comparing the obtained resonant frequencies with those of an isotropic host plate. Furthermore, for both FGM plate and FGM plate with piezoelectric layers, natural frequencies were obtained by finite element method. Very good agreement was observed between the results of finite element method and the method presented in this paper. Then for the two aforementioned types of boundary conditions, the values of power index were changed and its effect on the resonant frequencies was studied. Also, the effect of piezoelectric thickness layers on the natural frequencies of FGM piezoelectric plate was investigated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. F. E. Crawley and J. Luis, Use of piezoelectric actuators as elements of intelligent structures, AIAA. J. 25(10) (1987) 1373–1385.

    Article  Google Scholar 

  2. T. Takano and H. Hiroshi and T. Yoshro, Analysis of nonaxisymmetric vibration mode piezoelectric annular plate and its application to an ultrasonic motor, IEEE. Trans on Ultrasonic Ferroelectrics. 37(6) (1990) 558–565.

    Article  Google Scholar 

  3. H. Woo-Seok and C. P. Hyun, Finite element modeling of piezoelectric sensors and actuators, AIAA. J. 31(5) (1993) 930–937.

    Article  Google Scholar 

  4. W. Nesbit and J. V. Hagood and J. M. Andrew, Modeling of a piezoelectric rotary ultrasonic motor, IEEE Trans on Ultrasonic Ferroelectrics. 42(2) (1995) 210–224.

    Article  Google Scholar 

  5. P. Heyliger, Exact solutions for simply supported laminated piezoelectric plates, J. Appl. Mech. 64 (1997) 299–306.

    Article  MATH  Google Scholar 

  6. J. R. Friend and D. S. Stutts, The dynamics of an annular piezoelectric motor stator, J. Sound. Vib. 204(3) (1997) 421–437.

    Article  Google Scholar 

  7. P. Hagedorn and J. Wallashek, Traveling wave ultrasonic motors part I working principle and mathematical modeling of the stator, J. Sound. Vib. 155 (1992) 31–46.

    Article  Google Scholar 

  8. J. Wallashek P. Hagedorn and W. Konrad, 1993 Traveling wave ultrasonic motors part II: a numerical method for the flexural vibrations of the stator, J. Sound. Vib. 168 (1993) 115–122.

    Article  Google Scholar 

  9. J. E. Ashton and M. Whitney, Theory of Laminated Plates, Stanford, (1970).

  10. R. Szilard, Theory and analysis of plates-classical and numerical methods, Englewood Cliffs NJ: Prentice-Hall, (1974).

    MATH  Google Scholar 

  11. R. D. Mindlin, Influence of rotary inertia and shear on flexural motions of isotropic elastic plates, J. Appl Mech. Trans. ASME E 73 (1951) 31–38.

    Google Scholar 

  12. J. N. Reddy, A general third-order nonlinear theory of plates with moderate thickness, J. Nonlinear Mech. 25 (1990) 677–686.

    Article  MATH  Google Scholar 

  13. J. N. Reddy, A review of refined theories of laminated composite plates, Shock and Vib Digest, 22(7) (1990) 3–17.

    Article  Google Scholar 

  14. A. Nosier and R. K. Kapania and J. N. Reddy, Free vibration analysis of laminated plates using a layer wise theory, AIAA. J. 8 (1993) 2335–2346.

    Article  Google Scholar 

  15. D. Haojiang and et al, Free axisymmetric vibration of transversely isotropic piezoelectric circular plates, Int. J. Solids Struct. 36 (1999) 4629–4652.

    Article  MATH  Google Scholar 

  16. H. Deresiewicz and R. D. Mindlin, Axially symmetric flexural vibration of a circular disc, J. Appl. Mech. 22 (1995) 86–88.

    MathSciNet  Google Scholar 

  17. H. Deresiewicz, Symmetric flexural vibration of a clamped circular disc, J. Appl. Mech. 23 (1956) 319.

    Google Scholar 

  18. X. Liu and Q. Wang and S. T. Quek, Analytical solution for free vibration of piezoelectric coupled moderately thick circular plates, Int J. Solids Strut. 39 (2002) 2129–2151.

    Article  MATH  Google Scholar 

  19. S. Kapuria and P. C. Dumir, Geometrically nonlinear axisymmetric response of thin circular plate under piezoelectric actuation, J. Sound Vib. 10 (2005) 413–4123.

    Google Scholar 

  20. W. H. Duan and S. T. Quek and Q. Wang, Free vibration of piezoelectric coupled thin and thick annular plate, J. Sound Vib. 281 (2005) 119–139.

    Article  Google Scholar 

  21. A. Almajid and M. Taya and S. Hudunt, Analysis of out-of-plane displacement and stress field in a piezocomposite plate with functionally graded microstructure, Int. J. Solids Struct. 38 (2001) 3377–3391.

    Article  MATH  Google Scholar 

  22. C. P. Fung, Imperfection sensitivity in the nonlinear vibration of functionally graded plates, Euro. J. Mech. A/Solids. 25 (2005) 425–4236.

    Article  Google Scholar 

  23. J. J. Hsieh and L. T. Lee, An inverse problem for a functionally graded elliptical plate with large deflection and slightly distributed boundary, Int. J. Solids Struct. 43 (2006) 5981–5993.

    Article  MATH  Google Scholar 

  24. T. Parakash and M. Ganapathi, Asymmetric flexural vibration and thermoelastic stability of FGM circular plates using finite element method, Composite. B 37 (2006) 642–649.

    Google Scholar 

  25. J. Yang and S. Kitipornchai and K. M. Liew, Large amplitude vibration of thermo-electro-mechanically stressed FGM laminated plate, Comput. Meth. Appl. Mech. 192 (2003) 3861–3885.

    Article  MATH  Google Scholar 

  26. Q. Wang and S. T. Quek and X. Liu, Analysis of piezoelectric coupled circular plate, Smart. Mater. Struct. 10 (200) 229–239.

  27. D. O. Brush and B. O. Almroth, Buckling of Bars Plates and Shells, McGraw-Hill, New York, (1975).

    MATH  Google Scholar 

  28. J. N. Reddy, Theory and Analysis of Elastic Plates, Taylor and Francis, Philadelphia, (1999).

    Google Scholar 

  29. L. Meirovitch, Principles and Techniques of Vibrations, Prentice-Hall, international Inc, (1997).

  30. D. Halliday and R. Resniek, Physics, Jhon Wiley and Sons, (1978).

  31. H. F. Tiersten, Linear Piezoelectric Plate Vibrations, Plenum press, New York, (1978).

    Google Scholar 

  32. J. N. Reddy and G. N. Praveen, Nonlinear transient thermoelastic analysis of functionally graded ceramic- metal plate, Int. J. Solids Struct. 35 (1998) 4457–4476.

    Article  MATH  Google Scholar 

  33. R. C. Wetherhold and S. S. Wang, The use of functionally graded materials to eliminate or control thermal deformation, Composites Sci Tech. 6 (1996) 1099–1104.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Islamic Azad University, Science and Research Branch of Tehran, Tehran, Iran

    Saeed Jafari Mehrabadi

  2. Department of Mechanical Engineering, Sharif University of Technology, Tehran, Iran

    M. H. Kargarnovin

  3. Department of Mechanical Engineering, Azad University, Arak Branch, Azad, Iran

    M. M. Najafizadeh

Authors
  1. Saeed Jafari Mehrabadi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. H. Kargarnovin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. M. Najafizadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Saeed Jafari Mehrabadi.

Additional information

This paper was recommended for publication in revised form by Associate Editor Seockhyun Kim

Saeed Jafari Mehrabadi received his B.S. in mechanical Engineering from Azad University, Arak, Iran, in 1992. He then received his M.S. from Azad University, Tehran, Iran in 1995. Now he is a faculty member of the department of mechanical engineering in Azad university of Arak, Iran and PhD student of Azad University, Science and Research Campus, Pounak, Tehran, Iran. His interests include computational methods and solid mechanics such as vibration, buckling.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jafari Mehrabadi, S., Kargarnovin, M.H. & Najafizadeh, M.M. Free vibration analysis of functionally graded coupled circular plate with piezoelectric layers. J Mech Sci Technol 23, 2008–2021 (2009). https://doi.org/10.1007/s12206-009-0519-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-009-0519-9

Keywords

Search

Navigation