Skip to main content
SpringerLink
Log in

Dynamic behaviors of nonlinear fractional-order differential oscillator

  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

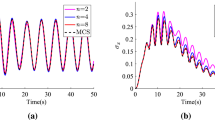
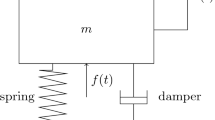
The nonlinear dynamic behaviors of oscillators described by fractional-order differential are presented in this paper. The background of the research is based upon two engineering practices. First is that the visco-elastic behaviors of some advanced polymeric materials can be accurately modeled by the fractional calculus constitutive law. Second is that the influence of nonlinear visco-elasticity described by the fractional operator cannot be neglected in some cases such as the vibration with large displacement or large strain and thermo-visco-elastic coupled problems. The numerical scheme for solving the nonlinear equation of motion is developed. The results show that because of the introduction of nonlinear damping modeled by the fractional-order operator, the bifurcation and chaos of the oscillator appear in forced vibration. Furthermore, the fraction value of the fractional operator evidently affects the dynamic behavior of the nonlinear fractional differential oscillator.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. K. Addolfsson, Mikael Enelund, S. Larsson, Models and numerical procedures for nonlinear fractional order viscoelastics fractional differentiation and its application, Germany: Bordeaux 1 University, ISBN:3-86608-026-3 (2005), 365–376.

    Google Scholar 

  2. Y. Meshaka, A. Stephane and C. Christian, Describing viscoelasticity using thermodynamic functions: link with fractional type operators, France: FDA04, 1st IFAC workshop on fractional differentiation and its application 19–21( 2004).

    Google Scholar 

  3. H. Nasuno and N. Shimizu, Nonlinear Statical and Dynamical Models of Fractional Derivative Viscoelastic Body, Proc. 2005 ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. September 24–28, Long Beach, California, USA(2005).

  4. H. Z. Sun, Constitutive law of viscoelastic materials modeled by fractional-order derivatives, Masterdegree thesis, JiNan University, China (2006, In Chinese).

    Google Scholar 

  5. Wei ZHANG and Nobuyuki SHIMIZU, Numerical Algorithm for Dynamic Problems Involving Fractional Operators, Int. J. of JSME, Ser. C, 41, NO.3, (1998)364–370.

    Google Scholar 

  6. John Guckenheimer and Philip Holmes, Nonlinear oscillations, dynamical systems and bifurcations of vector fields, Fifth Printing, New York: Springer-Verlag(1997).

    Google Scholar 

  7. W. Zhang, H. Xu and N. Shimizu, Numerical analysis formulation of viscoelastic solids modeled by fractional operator, ACTA MECHANICA SINICA, 36(5) Sept. (2004) 617–621 (In Chinese).

    Google Scholar 

  8. S. K. Liao and W. Zhang, Dynamics of fractional Duffing oscillator, Journal of Dynamics and Control, 6(2) (2008) 122–125 (In Chinese).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electronic Engineering, JiNan University, Guangzhou, China

    Wei Zhang

  2. Institute of Mechanical Science and Technology, Shenzhen, China

    Shao-kai Liao

  3. Department of Mechanical and Power Engineering, Iwaki Meisei University, Iwaki, Japan

    Nobuyuki Shimizu

Authors
  1. Wei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shao-kai Liao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nobuyuki Shimizu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wei Zhang.

Additional information

Wei Zhang received his doctorate degree in Mechanics at Xi’an Jiaotong University in China in 1994. He went to the University Of Sheffield in the UK as an academic visitor from July 1986 to July 1987. He completed his post-doctorate study in Iwaki Meisei University in Japan through the support of the JSPS from May 1997 to June 1999. Dr. Zhang is currently a professor at the Department of Electronic Engineering of JiNan University in Guangzhou, China.

Shao-kai Liao received his B.E. degree in Civil Engineering at JiNan University in Guangzhou, China in 2004 and his master’s degree in Engineering Mechanics at the same university in 2006. Mr. Liao was once a postgraduate student of Professor Wei Zhang, and he now works in an institute in Shenzhen City in China.

Nobuyuki Shimizu received his B.S. degree in Mechanical Engineering at Yokohama National University and his master’s and doctorate degrees in Mechanical Engineering at University of Tokyo in 1968 and 1971, respectively. He went to the California Institute of Technology in California, U.S.A. as a visiting associate from October 1976 to September 1977. Dr. Shimizu is currently a professor at the Department of Mechanical and Power Engineering of Iwaki Meisei University in Japan.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhang, W., Liao, Sk. & Shimizu, N. Dynamic behaviors of nonlinear fractional-order differential oscillator. J Mech Sci Technol 23, 1058–1064 (2009). https://doi.org/10.1007/s12206-009-0341-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-009-0341-4

Keywords

Search

Navigation