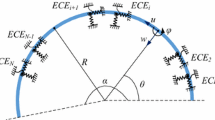
Abstract
A finite thin circular beam element for the out-of-plane vibration analysis of curved beams is presented in this paper. Its stiffness matrix and mass matrix are derived, respectively, from the strain energy and the kinetic energy by using the natural shape functions derived from an integration of the differential equations in static equilibrium. The matrices are formulated with respect to the local polar coordinate system or to the global Cartesian coordinate system in consideration of the effects of shear deformation and rotary inertias. Some numerical examples are analyzed to confirm the validity of the element. It is shown that this kind of finite element can describe quite efficiently and accurately the out-of-plane motion of thin curved beams.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
R. Davis, R. D. Henshell and G. B. Warburton, Curved beam finite elements for coupled bending and torsional vibration, Earth. Eng. and Struct. Dynamics 1 (1972) 165–175.
C. H. Yoo and J. P. Ferenbach, Natural frequencies of curved girders, J. Eng. Mech. Div. ASCE 107(EM2) (1981) 339–354.
R. Palaninathan and P. S. Chandrasekharan, Curved beam element stiffness matrix formulation, Comp. and Struct. 21(4) (1985) 663–669.
A. O. Lebeck and J. S. Knowlton, A finite element for the three-dimensional deformation of a circular ring, Int. J. Num. Methods Eng. 21 (1985) 421–435.
J. K. Choi and J. K. Lim, General curved beam elements based on the assumed strain fields, Comp. and Struct. 55(3) (1995) 379–386.
J. S. Wu and L. K. Chiang, Out-of-plane responses of a circular curved Timoshenko beam due to a moving load, Int. J. Solids Structures 40 (2003) 7425–7448.
C. B. Kim, J. W. Park, S. Kim and C. Cho, A finite thin circular beam element for in-plane vibration analysis of curved beams, J. Mech. Sci. and Tech. 19(12) (2005) 2187–2196.
I. S. Sokolnikoff, Mathematical Theory of Elasticity, McGraw-Hill, New York, USA, (1956).
G. R. Cowper, The shear coefficient in Timoshenko’s beam theory, J. Appl. Mech. 33 (1966) 335–340.
S. S. Rao, Effects of transverse shear and rotary inertia on the coupled twist-bending vibrations of circular rings, J. Sound Vibration. 16(4) (1971) 551–566.
J. Kirkhope, Out-of-plane vibration of thick circular ring, J. Eng. Mech. Div. ASCE 102(EM2) (1976) 239–247.
W. P. Howson and A. K. Jemah, Exact out-of-plane natural frequencies of curved Timoshenko beams, J. Eng. Mech. 125(1) (1999) 19–25.
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper was recommended for publication in revised form by Associate Editor Seockhyun Kim
Chang-Boo Kim received his B.S. degree in Mechanical Engineering from Seoul University, Korea in 1973. He then received his D.E.A., Dr.-Ing. and Dr.-es-Science degrees from Nantes University, France in 1979, 1981 and 1984, respectively. Dr. Kim is currently a Professor at the School of Mechanical Engineering at Inha University in Incheon, Korea. His research interests are in the area of vibrations, structural dynamics, and MEMS.
Rights and permissions
About this article
Cite this article
Kim, B.Y., Kim, CB., Song, S.G. et al. A finite thin circular beam element for out-of-plane vibration analysis of curved beams. J Mech Sci Technol 23, 1396–1405 (2009). https://doi.org/10.1007/s12206-008-1213-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12206-008-1213-2