Skip to main content
SpringerLink
Log in

A Stochastic Dual Response Surface Method for Reliability Analysis Considering the Spatial Variability

  • Structural Engineering
  • Published:
KSCE Journal of Civil Engineering Aims and scope Submit manuscript

Abstract

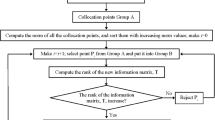
To solve spectral stochastic finite element problems, the collocation-based spectral stochastic finite element method (SSFEM) was developed, and the Stochastic Response Surface Method (SRSM) was used to represent uncertainty propagation. Therefore, the accuracy of SRSM is important for obtaining more accurate probabilistic results. The weighted SRSM was developed to improve the global accuracy of SRSM, but it is not suitable for random field problems because weights might distort the response surface. In this study, a new Stochastic Dual-response Surface Method (SDRSM) was developed to improve the accuracy of SRSM. The SDRSM combines the conventional SRSM and target-weighted SRSM (TWSRSM), which is assigned a weight for the numerical result corresponding to the collocation point. Then, the proposed method was extended to deal with problems involving random fields. For comparison with the conventional methods (SRSM and WSRSM), two numerical examples involving random fields were carried out. Compared with Monte Carlo simulation results, SDRSM shows the smallest error without the addition of the collocation points. In addition, the mean absolute errors for equally spaced probability intervals were compared, and their mean and standard deviation of SDRSM were relatively smaller than that of other methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Adomian, G. (1994). Solving Frontier Problems of Physics: The Decomposition Method, Kluwer, Boston.

    Book  MATH  Google Scholar 

  • Arregui-Mena, J. D., Margetts, L., and Mummery, P. M. (2016). “Practical application of the stochastic finite element method.” Arch. Comput. Method E., Vol. 23, No. 1, pp. 171–190, DOI: 10.1007/s11831-014-9139-3.

    Article  MathSciNet  MATH  Google Scholar 

  • Blatman, G. and Sudret, B. (2011). “Adaptive sparse polynomial chaos expansion based on least angle regression.” J. Comput. Phys., Vol. 230, No. 6, pp. 2345–2367, DOI: 10.1016/j.jcp.2010.12.021.

    Article  MathSciNet  MATH  Google Scholar 

  • Bellomo, N. and Riganti, R. (1987). Nonlinear Stochastic Systems in Physics and Mechanics, World Scientific, Singapore.

    Book  MATH  Google Scholar 

  • Belytschko, T., Organ, D., and Krongauz, Y. (1995). “A coupled finite element-element-free Galerkin method.” Comput. Mech., Vol. 17, No. 3, pp. 186–195, DOI: 10.1007/BF00364080.

    Article  MathSciNet  MATH  Google Scholar 

  • Benaroya, H. and Rehak, M. (1987). “Parametric random excitation. I: Exponentially correlated parameters.” J. Eng. Mech., Vol. 113, No. 6, pp. 861–874, DOI: 10.1061/(ASCE)0733-9399(1987)113:6(861).

    Article  Google Scholar 

  • Do, D. M., Gao, W., and Song, C. M. (2016). “Stochastic finite element analysis of structures in the presence of multiple imprecise random field parameters.” Comput. Methods Appl. Mech. Engrg., Vol. 300 (2016) pp. 657–688, DOI: 10.1016/j.cma.2015.11.032.

    Article  MathSciNet  Google Scholar 

  • Drakos, S. and Pande, G. N. (2016). “Stochastic finite element analysis using polynomial Chaos.” Studia Geotechnica et Mechanica, Vol. 38, No. 1, pp. 33–43, DOI: 10.1515/sgem-2016-0004.

    Article  Google Scholar 

  • Ghanem, R. G. and Spanos, P. D. (1991). Stochastic Finite Elements: A Spectral Approach, Springer, New York.

    Book  MATH  Google Scholar 

  • Ghosh, D. and Iaccarino, G. (2007). “Applicability of the spectral stochastic finite element method in time-dependent uncertain problems.” Annual Research Briefs 2007, pp. 133–141.

    Google Scholar 

  • Grigoriu, M. (2006). “Evaluation of Karhunen-Loève, spectral and sampling representations for stochastic processes.” J. Eng. Mech., Vol. 132, No. 2, pp. 179–189, DOI: 10.1061/(ASCE)0733-9399 (2006)132:2(179).

    Article  Google Scholar 

  • Hemanth, G., Vinoy, K. J., and Gopalakrishnan, S. (2014). “Spectral stochastic finite element method for periodic structure.” 2014 IEEE International Microwave and RF Conference (IMaRC), pp. 9–12, DOI: 10.1109/IMaRC.2014.7038959.

    Chapter  Google Scholar 

  • Huang, S., Mahadevan, S., and Rebba, R. (2007). “Collocation-based stochastic finite element analysis for random field problems.” Probabilist. Eng. Mech., Vol. 22, No. 2, pp. 194–205, DOI: 10.1016/j.probengmech.2006.11.004.

    Article  Google Scholar 

  • Isukapalli, S. S., Roy, A., and Georgopoulos, P. G. (1998). “Stochastic Response Surface Methods (SRSMs) for uncertainty propagation: application to environmental and biological systems.” Risk. Anal., Vol. 18, No. 3, pp. 351–363, DOI: 10.1111/j.1539-6924.1998.tb01301.

    Article  Google Scholar 

  • Jahedi, A. and Ahmadi, G. (1983). “Application of Wiener–Hermite expansion to nonstationary random vibrations of a Duffing Oscillator.” J. Appl. Mech., Vol. 50, No. 2, pp. 436–442, DOI: 10.1115/1.3167056.

    Article  MathSciNet  MATH  Google Scholar 

  • Kaminski, M. (2013). The Stochastic Perturbation Method for Computational Mechanics, John Wiley & Sons, New Jersey.

    Book  MATH  Google Scholar 

  • Myers, R. H. and Montgomery, D. C. (1995). In: Response surface methodology: Process and product optimization using designed experiments, John Wiley & Sons, New Jersey.

    MATH  Google Scholar 

  • Pascual, B. and Adhikari, S. (2012). “A reduced polynomial chaos expansion method for the stochastic finite element analysis.” Sadhana, Vol. 37, No. 3, pp 319–340, DOI: 10.1007/s12046-012-0085-1.

    Article  MathSciNet  MATH  Google Scholar 

  • Pukl, R., Jansta, M., Cervenka, J., Vorechovský, M., Novák, D., and Rusina, R. (2006). “Spatial variability of material properties in nonlinear computer simulation.” Proceedings of the EURO-C Conference, Mayrhofen, Austria, pp. 891–896.

    Google Scholar 

  • Spanos, P. D., Beer, M., and Red-Horse, J. (2007). “Karhunen–Loéve Expansion of Stochastic Processes with a Modified Exponential Covariance Kernel." J. Eng. Mech., Vol. 133, No. 7, pp. 773–779, DOI: 10.1061/(ASCE)0733-9399(2007)133:7(773).

    Article  Google Scholar 

  • Spanos, P. D. and Ghanem, R. G. (1989). “Stochastic finite element expansion for random media.” J. Eng. Mech., Vol. 115, No. 5, pp. 1035–1053, DOI: 10.1061/(ASCE)0733-9399(1989)115:5(1035).

    Article  Google Scholar 

  • Stefanou, G. (2009). “The stochastic finite element method: Past, present and future.” Comput. Methods Appl. Mech. Eng., Vol. 198, Nos. 9–12, pp. 1031–1051, DOI: 10.1016/j.cma.2008.11.007.

    Article  MATH  Google Scholar 

  • Stefanou, G. and Papadrakakis, M. (2007). “Assessment of spectral representation and Karhunen–Loève expansion methods for the simulation of Gaussian stochastic fields.” Comput. Methods Appl. Mech. Eng., Vol. 196, Nos. 21–24, pp. 2465–2477, DOI: 10.1016/j.cma.2007.01.009.

    Article  MATH  Google Scholar 

  • Sudret, B. and Der Kiureghian, A. (2000). Stochastic finite element methods and reliability: A state-of-the-art Report, Technical Report on UCB/SEMM-2000/08, Department of Civil and Environmental Engineering, UC Berkeley.

    Google Scholar 

  • Tatang, M. A. (1995). Direct Incorporation of Uncertainty in Chemical and Environmental Engineering Systems, PhD Thesis, Massachusetts Institute of Technology.

    Google Scholar 

  • Vanmarcke, E. and Grigoriu, M. (1983). “Stochastic finite element analysis of simple beams.” J. Eng. Mech., Vol. 109, No. 5, pp. 1203–1214, DOI: 10.1061/(ASCE)0733-9399(1983)109:5(1203).

    Article  Google Scholar 

  • Villadsen, J. and Michelsen, M. L. (1978). Solution of differential equation models by polynomial approximation, Prentice-Hall, Englewood Cliffs, New Jersey.

    MATH  Google Scholar 

  • Xiong, F., Chen, W., Xiong, Y., and Yang, S. (2011). “Weighted stochastic response surface method considering sample weights.” Struct. Multidiscip. Optim., Vol. 43, No. 6, pp. 837–849, DOI: 10.1007/s00158-011-0621-3.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dept. of Civil and Construction Engineering, Oregon State University, Oregon, USA

    Taeho Bong

  2. Dept. of Rural Systems Engineering, and Research Institute for Agriculture & Life Sciences, Seoul National University, Seoul, 08826, Korea

    Younghwan Son

Authors
  1. Taeho Bong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Younghwan Son
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Younghwan Son.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bong, T., Son, Y. A Stochastic Dual Response Surface Method for Reliability Analysis Considering the Spatial Variability. KSCE J Civ Eng 22, 3524–3533 (2018). https://doi.org/10.1007/s12205-018-0803-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12205-018-0803-2

Keywords

Search

Navigation