Skip to main content
SpringerLink
Log in

Nonlinear Finite Element Method Considering Martensite Plasticity For Shape Memory Alloy Structure

  • Published:
Journal of Shanghai Jiaotong University (Science) Aims and scope Submit manuscript

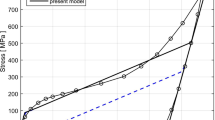
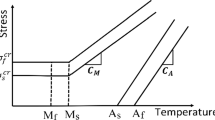
Abstract

This work presents a nonlinear finite element method to simulate the macroscopic mechanical responses and the effects of martensite plasticity in a shape memory alloy (SMA) structure. A linear relationship formulation is adopted to express the influence of martensite plasticity on the inverse martensitic phase transition of SMA material. Incorporating with a trigonometric-type phase transition evolution law and an exponential-type plastic flow evolution law, an incremental mechanical model with two internal variables is supposed based on the macroscopic experimental phenomena. A nonlinear finite element equation is formulated and solved by the principle of virtual displacement and Newton-Raphson method respectively. By employing the proposed nonlinear finite element method, the uniform tensile bar and three-point bending beam are simulated and analyzed. Results illustrate that the presented nonlinear finite element method is suitable to act as an effective computational tool for the wide applications based on the SMA material considering the effects of martensite plasticity because all material constants related to the method can be obtained from macroscopic experiments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

a :

Nodal displacement matrix

A f :

Austenite finishing temperature, °C

A s :

Austenite starting temperature, °C

B :

Geometric matrix

C A :

Stress-temperature relation coefficient of austenite, MPa/°C

C M :

Stress-temperature relation coefficient of martensite, MPa/°C

\(\hat{\boldsymbol{D}}\) :

Tangent elastic matrix

D e :

Elastic matrix

E :

Elastic modulus, MPa

E a :

Austenite elastic modulus, MPa

E m :

Martensite elastic modulus, MPa

F p :

Direction vector of plastic incremental strain

F tr :

Direction vector of phase transition incremental strain

H p :

Plastic tangent modulus, MPa

H tr :

Phase transition tangent modulus, MPa

J :

Jacobian matrix

M s :

Martensite starting temperature, °C

P :

Nodal load matrix

T :

Ambient temperature, °C

α :

Thermal expansion coefficient, (°C)−1

ε :

Total strain

ε e :

Elastic strain

ε L :

Maximum phase transition strain

ε p :

Plastic strain

\({\bar \varepsilon ^{\rm{p}}}\) :

Equivalent plastic strain

ε pc :

Critical plastic strain

ε th :

Thermal strain

ε tr :

Phase transition strain

\({\bar \varepsilon ^{{\rm{tr}}}}\) :

Equivalent phase transition strain

Λ :

Thermal expansion vector

ξ :

Volume fraction of martensite

ξ s :

Volume fraction of stress-induced martensite or detwinned martensite

ξ us :

Volume fraction of unrecoverable stress-induced martensite or detwinned martensite

σ :

Stress, MPa

\(\bar \sigma \) :

Equivalent stress, MPa

σ af :

Austenite finishing stress, MPa

σ as :

Austenite starting stress, MPa

σ crf :

Initial martensite finishing stress, MPa

σ crs :

Initial martensite starting stress, MPa

σ mf :

Martensite finishing stress, MPa

σ ms :

Martensite starting stress, MPa

σ yc :

Yield stress, MPa

φ p :

Plastic potential

φ tr :

Phase transition potential

References

  1. ZHOU B, YOON S H, LENG J S. A three-dimensional constitutive model for shape memory alloy [J]. Smart Materials and Structures, 2009, 18(9): 095016.

    Article  Google Scholar 

  2. RULAND A, TAYLOR J M, ZILLINGER C. Convex integration arising in the modelling of shape-memory alloys: Some remarks on rigidity, flexibility and some numerical implementations [J]. Journal of Nonlinear Science, 2019, 29: 2137–2184.

    Article  MathSciNet  Google Scholar 

  3. DELLA PORTA F. Analysis of a moving mask hypothesis for martensitic transformations [J]. Journal of Nonlinear Science, 2019, 29: 2341–2384.

    Article  MathSciNet  Google Scholar 

  4. TANAKA K. Thermomechanical sketch of shape memory effect: One-dimensional tensile behavior [J]. Res Mechanica: International Journal of Structural Mechanics and Materials Science, 1986, 18(3): 251–263.

    Google Scholar 

  5. LIANG C, ROGERS C A. One-dimensional thermo-mechanical constitutive relations for shape memory materials [J]. Journal of Intelligent Material Systems and Structures, 1990, 1(2): 207–234.

    Article  Google Scholar 

  6. BOYD J G, LAGOUDAS D C. Thermomechanical response of shape memory composites [J]. Journal of Intelligent Material Systems and Structures, 1994, 5(3): 333–346.

    Article  Google Scholar 

  7. BRINSON L C. One-dimensional constitutive behavior of shape memory alloys: Thermomechanical derivation with non-constant material functions and redefined martensite internal variable [J]. Journal of Intelligent Material Systems and Structures, 1993, 4(2): 229–242.

    Article  Google Scholar 

  8. LIM T J, MCDOWELL D L. Mechanical behavior of an Ni-Ti shape memory alloy under axial-torsional proportional and nonproportional loading [J]. Journal of Engineering Materials and Technology, 1999, 121(1): 9–18.

    Article  Google Scholar 

  9. PENG X, YANG Y, HUANG S. A comprehensive description for shape memory alloys with a two-phase constitutive model [J]. International Journal of Solids and Structures, 2001, 38(38/39): 6925–6940.

    Article  Google Scholar 

  10. ZHOU B, YOON S H. A new phase transformation constitutive model of shape memory alloys [J]. Smart Materials and Structures, 2006, 15(6): 1967–1973.

    Article  Google Scholar 

  11. MIRZAEIFAR R, DESROCHES R, YAVARI A. A combined analytical, numerical, and experimental study of shape-memory-alloy helical springs [J]. International Journal of Solids and Structures, 2011, 48(3/4): 611–624.

    Article  Google Scholar 

  12. MERZOUKI T, DUVAL A, BEN ZINEB T. Finite Element analysis of a shape memory alloy actuator for a micropump [J]. Simulation Modelling Practice and Theory, 2012, 27: 112–126.

    Article  Google Scholar 

  13. CHEMISKY Y, CHATZIGEORGIOU G, KUMAR P, et al. A constitutive model for cyclic actuation of high-temperature shape memory alloys [J]. Mechanics of Materials, 2014, 68: 120–136.

    Article  Google Scholar 

  14. GU X, ZAKI W, MORIN C, et al. Time integration and assessment of a model for shape memory alloys considering multiaxial nonproportional loading cases [J]. International Journal of Solids and Structures, 2015, 54: 82–99.

    Article  Google Scholar 

  15. HAZAR S, ZAKI W, MOUMNI Z, et al. Modeling of steady-state crack growth in shape memory alloys using a stationary method [J]. International Journal of Plasticity, 2015, 67: 26–38.

    Article  Google Scholar 

  16. PERAZA HERNANDEZ E A, KIEFER B, HARTL D J, et al. Analytical investigation of structurally stable configurations in shape memory alloy-actuated plates [J]. International Journal of Solids and Structures, 2015, 69/70: 442–458.

    Article  Google Scholar 

  17. LONG X, PENG X, FU T, et al. A micro-macro description for pseudoelasticity of NiTi SMAs subjected to nonproportional deformations [J]. International Journal of Plasticity, 2017, 90: 44–65.

    Article  Google Scholar 

  18. KANG Z T, ZHOU B, XUE S F. Finite element numerical simulation on thermo-mechanical coupling behavior in shape memory alloy pipe connection [J]. Journal of Mechanical Engineering, 2018, 54(18): 68–75 (in Chinese).

    Article  Google Scholar 

  19. ARMATTOE K M, BOUBY C, HABOUSSI M, et al. Modeling of latent heat effects on phase transformation in shape memory alloy thin structures [J]. International Journal of Solids and Structures, 2016, 88/89: 283–295.

    Article  Google Scholar 

  20. WANG J, MOUMNI Z, ZHANG W, et al. A thermomechanically coupled finite deformation constitutive model for shape memory alloys based on Hencky strain [J]. International Journal of Engineering Science, 2017, 117: 51–77.

    Article  MathSciNet  Google Scholar 

  21. LEI H S, WANG Z Q, ZHOU B, et al. Simulation and analysis of shape memory alloy fiber reinforced composite based on cohesive zone model [J]. Materials & Design, 2012, 40: 138–147.

    Article  Google Scholar 

  22. GU D, HE B. Finite element simulation and experimental investigation of residual stresses in selective laser melted Ti-Ni shape memory alloy [J]. Computational Materials Science, 2016, 117: 221–232.

    Article  Google Scholar 

  23. ARMATTOE K M, HABOUSSI M, BEN ZINEB T. A 2D finite element based on a nonlocal constitutive model describing localization and propagation of phase transformation in shape memory alloy thin structures [J]. International Journal of Solids and Structures, 2014, 51(6): 1208–1220.

    Article  Google Scholar 

  24. HASSANLI S, SAMALI B. Buckling analysis of laminated composite curved panels reinforced with linear and non-linear distribution of Shape Memory Alloys [J]. Thin-Walled Structures, 2016, 106: 9–17.

    Article  Google Scholar 

  25. HATEFI ARDAKANI S, AFSHAR A, MOHAMMADI S. Numerical study of thermo-mechanical coupling effects on crack tip fields of mixed-mode fracture in pseudoelastic shape memory alloys [J]. International Journal of Solids and Structures, 2016, 81: 160–178.

    Article  Google Scholar 

  26. JIANG D J, BECHLE N J, LANDIS C M, et al. Buckling and recovery of NiTi tubes under axial compression [J]. International Journal of Solids and Structures, 2016, 80: 52–63.

    Article  Google Scholar 

  27. KATANCHI B, CHOUPANI N, KHALIL-ALLAFI J, et al. Photostress analysis of stress-induced martensite phase transformation in superelastic NiTi [J]. Materials Science and Engineering: A, 2017, 688: 202–209.

    Article  Google Scholar 

  28. ZHANG Y Q, JIANG S Y, ZHAO Y N, et al. Simulation of isothermal precision extrusion of NiTi shape memory alloy pipe coupling by combining finite element method with cellular automaton [J]. Journal of Central South University, 2017, 24: 506–514.

    Article  Google Scholar 

  29. YU C, KANG G Z, KAN Q H, et al. A micromechanical constitutive model based on crystal plasticity for thermo-mechanical cyclic deformation of NiTi shape memory alloys [J]. International Journal of Plasticity, 2013, 44: 161–191.

    Article  Google Scholar 

  30. YU C, KANG G Z, KAN Q H. A micromechanical constitutive model for anisotropic cyclic deformation of super-elastic NiTi shape memory alloy single crystals [J]. Journal of the Mechanics and Physics of Solids, 2015, 82: 97–136.

    Article  MathSciNet  Google Scholar 

  31. ASHRAFI M J, ARGHAVANI J, NAGHDABADI R, et al. Theoretical and numerical modeling of dense and porous shape memory alloys accounting for coupling effects of plasticity and transformation [J]. International Journal of Solids and Structures, 2016, 88/89: 248–262.

    Article  Google Scholar 

  32. PARANJAPE H M, MANCHIRAJU S, ANDERSON P M. A phase field — Finite element approach to model the interaction between phase transformations and plasticity in shape memory alloys [J]. International Journal of Plasticity, 2016, 80: 1–18.

    Article  Google Scholar 

  33. HU L, JIANG S, SHI L, et al. Prediction of grain scale plasticity of NiTi shape memory alloy based on crystal plasticity finite element method [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(4): 775–784.

    Article  Google Scholar 

  34. CISSÉ C, ZAKI W, GU X, et al. A nonlinear 3D model for iron-based shape memory alloys considering different thermomechanical properties for austenite and martensite and coupling between transformation and plasticity [J]. Mechanics of Materials, 2017, 107: 1–21.

    Article  Google Scholar 

  35. WANG X M, XU B X, YUE Z F. Micromechanical modelling of the effect of plastic deformation on the mechanical behaviour in pseudoelastic shape memory alloys [J]. International Journal of Plasticity, 2008, 24(8): 1307–1332.

    Article  Google Scholar 

  36. ZHOU B. A macroscopic constitutive model of shape memory alloy considering plasticity [J]. Mechanics of Materials, 2012, 48: 71–81.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Engineering Mechanics, College of Pipeline and Civil Engineering, China University of Petroleum, Qingdao, Shandong, 266580, China

    Bo Zhou  (周博), Zetian Kang  (康泽天), Zhiyong Wang  (王志勇) & Shifeng Xue  (薛世峰)

Authors
  1. Bo Zhou  (周博)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zetian Kang  (康泽天)
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhiyong Wang  (王志勇)
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Shifeng Xue  (薛世峰)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bo Zhou  (周博).

Additional information

Foundation item: the National Key Research and Development Program of China (No. 2017YFC0307604)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, B., Kang, Z., Wang, Z. et al. Nonlinear Finite Element Method Considering Martensite Plasticity For Shape Memory Alloy Structure. J. Shanghai Jiaotong Univ. (Sci.) 26, 774–785 (2021). https://doi.org/10.1007/s12204-021-2327-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12204-021-2327-z

Key words

CLC number

Search

Navigation