Abstract
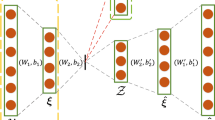
Sum-product networks (SPNs) are an expressive deep probabilistic architecture with solid theoretical foundations, which allows tractable and exact inference. SPNs always act as black-box inference machine in many artificial intelligence tasks. Due to their recursive definition, SPNs can also be naturally employed as hierarchical feature extractors. Recently, SPNs have been successfully employed as autoencoder framework in representation learning. However, SPNs autoencoder ignores the model structural duality and trains the models separately and independently. In this work, we propose a Dual-SPNs autoencoder which designs two SPNs autoencoders to compose as a dual form. This approach trains the models simultaneously, and explicitly exploits the structural duality between them to enhance the training process. Experimental results on several multilabel classification problems demonstrate that Dual-SPNs autoencoder is very competitive against with state-of-the-art autoencoder architectures.
Similar content being viewed by others
References
CHOI A, DARWICHE A. On relaxing determinism in arithmetic circuits [C]//34th International Conference on Machine Learning. Sydney, Australia: IMLS, 2017: 825–833.
POON H, DOMINGOS P. Sum-product networks: A new deep architecture [C]//IEEE International Conference on Computer Vision Workshops. Barcelona, Spain: IEEE, 2011: 689–690.
CHENG W C, KOK S, PHAM H V, et al. Language modeling with sum-product networks [C]//International Annual Conference of the International Speech Communication Association. Singapore: ISCA, 2014: 2098–2102.
AMER M R, TODOROVIC S. Sum product networks for activity recognition [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(4): 800–813.
VERGARI A, PEHARZ R, DI MAURO N, et al. Sumproduct autoencoding: Encoding and decoding representations using sum-product networks [C]//32nd Conference on Artificial Intelligence. New Orleans, USA: AAAI, 2018: 4163–4170.
XIA Y, HE D, QIN T, et al. Dual learning for machine translation [C]//30th Conference on Neural Information Processing Systems. Barcelona, Spain: MIT Press, 2016: 820–828.
YI Z, ZHANG H, TAN P, et al. DualGAN: Unsupervised dual learning for image-to-image translation [C]//IEEE International Conference on Computer Vision. Venice, Italy: IEEE, 2017: 2868–2876.
GENS R, DOMINGOS P. Learning the structure of sum-product networks [C]//30th International Conference on Machine Learning. Atlanda, USA: IMLS, 2013: 873–880.
ZHAO H, POUPART P, GORDON G. A unified approach for learning the parameters of sum-product networks [C]//30th Annual Conference on Neural Information Processing Systems. Barcelona, Spain: MIT Press, 2016: 433–441.
RASHWAN A, ZHAO H, POUPART P. Online and distributed Bayesian moment matching for parameter learning in sum-product networks [C]//19th International Conference on Artificial Intelligence and Statistics. Cadiz, Spain: Committee of AISTATS, 2016: 1469–1477.
ZHAO H, ADEL T, GORDON G, et al. Collapsed variational inference for sum-product networks [C]//33rd International Conference on Machine Learning. New York, USA: IMLS, 2016: 1310–1318.
ADEL T, BALDUZZI D, GHODSI A. Learning the structure of sum-product networks via an SVD-based algorithm [C]//31st Conference on Uncertainty in Artificial Intelligence. Amsterdam, the Netherlands: AUAI, 2015: 32–41.
MELIBARI M, POUPART P, DOSHI P, et al. Dynamic sum product networks for tractable inference on sequence data [C]//8th Conference on Probabilistic Graphical Models. Lugano, Switzerland: IDSIA, 2016: 345–355.
BOYD S, VANDENBERGHE L. Convex optimization [M]. Cambridge, UK: Cambridge University Press, 2004.
VERGARI A, DI MAURO N, ESPOSITO F. Simplifying, regularizing and strengthening sum-product network structure learning [M]//Machine learning and knowledge discovery in databases. Cham: Springer, 2015: 343–358.
KINGMA D, BA J. ADAM: A method for stochastic optimization [C]//3rd International Conference on Learning Representation. San Diego, USA: Committee of ICLR, 2015: 1–15.
BARTLETT P L, MENDELSON S. Rademacher and Gaussian complexities: Risk bounds and structural results [J]. Journal of Machine Learning Research, 2003, 3: 463–482.
FINLEY T, JOACHIMS T. Training structural SVMs when exact inference is intractable [C]//Proceedings of the 25th International Conference on Machine Learning. Helsinki, Finland: IMLS, 2008: 304–311.
GERMAIN M, GREGOR K, MURRAY I, et al. MADE: Masked autoencoder for distribution estimation [C]//32nd International Conference on Machine Learning. Lille, France: IMLS, 2015: 881–889.
WICKER J, TYUKIN A, KRAMER S. A nonlinear label compression and transformation method for multilabel classification using autoencoders [M]//Advances in knowledge discovery and data mining. Cham: Spinger, 2016: 328–340.
RIFAI S, VINCENT P, MULLER X, et al. Contractive auto-encoders: Explicit invariance during feature extraction [C]//28th International Conference on Machine Learning. Bellevue, USA: IMLS, 2011: 833–840.
VINCENT P, LAROCHELLE H, LAJOIE I, et al. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion [J]. Journal of Machine Learning Research, 2010, 11: 3371–3408.
DI MAURO N, VERGARI A, ESPOSITO F. Multilabel classification with cutset networks [C]//8th Conference on Probabilistic Graphical Models. Lugano, Switzerland: IDSIA, 2016: 147–158.
DEMBCZYŃSKI K, WAEGEMAN W, CHENG W W, et al. On label dependence and loss minimization in multi-label classification [J]. Machine Learning, 2012, 88: 5–45.
Author information
Authors and Affiliations
Corresponding author
Additional information
Foundation item: the National Natural Science Foundation of China (No. 61472161), and the Science & Technology Development Project of Jilin Province (Nos. 20180101334JC and 20160520099JH))
Rights and permissions
About this article
Cite this article
Wang, S., Zhang, H. & Chen, J. Dual Sum-Product Networks Autoencoder for Multi-Label Classification. J. Shanghai Jiaotong Univ. (Sci.) 25, 665–673 (2020). https://doi.org/10.1007/s12204-020-2204-1
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12204-020-2204-1