Skip to main content
SpringerLink
Log in

Discretization Methods of a Rotating Flexible Rectangular Thin Plate

  • Published:
Journal of Shanghai Jiaotong University (Science) Aims and scope Submit manuscript

Abstract

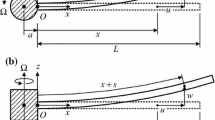
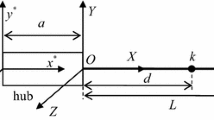
The rigid-flexible coupling dynamic modeling theory and the discretization methods of a rotating flexible rectangular thin plate are investigated in this paper. Based on the continuum mechanics, the rigid-flexible coupling dynamic model is established for the flexible rectangular thin plate undergoing large overall rotation, and the coupling term of the deformation which is caused by transverse deformation is considered. Assumed mode method (AMM), spline finite point method (SFPM) and Beizer finite point method (BFPM) are used to describe the deformation of the flexible rectangular plate, and then the dynamic equations of a rotating flexible rectangular thin plate undergoing overall motion are derived by Lagrange’s equation of the second kind. The dynamics of a cantilever plate undergoing large overall rotation is simulated via using different dynamic models, and the simulation results of the first order approximation model are compared with those of the traditional zero-order approximation model. It is shown that the first order approximation model with the dynamic stiffening terms can correctly describe the dynamic behavior of the system undergoing large overall rotation, while the zero-order approximation model cannot get the correct results. And AMM, SFPM, BFPM can well describe the deformation of a rotating flexible rectangular plate.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. KANE T R, RYAN R, BANERJEE A K. Dynamics of a cantilever beam attached to a moving base [J]. Journal of Guidance, Control, and Dynamics, 1987, 10(2): 139–151.

    Article  Google Scholar 

  2. BANERJEE A K, KANE T R. Dynamics of a plate in large overall motion [J]. Journal of Applied Mechanics, 1989, 56(4): 887–892.

    Article  Google Scholar 

  3. JIANG L Z, HONG J Z. Dynamics of thin elastic plates in large overall motions considering geometric non-linearity and coupling deformation [J]. Acta Me-chanica Sinica, 1999, 31(2): 243–249 (in Chinese).

    Google Scholar 

  4. ZHANG D J, HUSTON R L. On dynamic stiffening of flexible bodies having high angular velocity [J]. Mechanics of Structures and Machines, 1996, 24(3): 313–329.

    Article  Google Scholar 

  5. YOO H H, CHUNG J. Dynamics of rectangular plates undergoing prescribed overall motion [J]. Journal of Sound and Vibration, 2001, 239(1): 123–137.

    Article  Google Scholar 

  6. LI L, ZHANG D G. Free vibration analysis of rotating functionally graded rectangular plates [J]. Composite Structures, 2016, 136: 493–504.

    Article  Google Scholar 

  7. LIU Y W, WANG J M, ZHANG D J, et al. Dynamic analysis of rectangular plates undergoing large overall motion [J]. Journal of Vibration and Shock, 1998, 17(1): 38–43 (in Chinese).

    Google Scholar 

  8. ZHAO F Y, HONG J Z, LIU J Y, et al. Dynamic modeling and modal truncation approach for a high-speed rotating thin elastic rectangular plate [J]. Journal of Vibration Engineering, 2006, 19(3): 416–421 (in Chinese).

    Google Scholar 

  9. LIU J Y, PAN K Q. Rigid-flexible-thermal coupling dynamic formulation for satellite and plate multibody system [J]. Aerospace Science and Technology, 2016, 52: 102–114.

    Article  Google Scholar 

  10. LIU J Y, HONG J Z. Dynamic modeling theory and finite element method for a rectangular plate undergoing large overall motion [J]. Journal of Vibration Engineering, 2003, 16(2): 175–179 (in Chinese).

    Google Scholar 

  11. QIN R. Spline finite point method for analysis of laminated composite plates and shells [J]. Engineering Mechanics, 2001, 18(1): 14–23 (in Chinese).

    Google Scholar 

  12. LI S B, HUANG L X, JIANG L J, et al. A bidirectional B-spline finite point method for the analysis of piezoelectric laminated composite plates and its application in material parameter identification [J]. Composite Structures, 2014, 107: 346–362.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical-Electronic and Power Engineering, Jiangsu University of Science and Technology, Zhangjiagang, 215600, Jiangsu, China

    Jihua Fan  (范纪华)

  2. Suzhou Institute of Technology, Jiangsu University of Science and Technology, Zhangjiagang, 215600, Jiangsu, China

    Jihua Fan  (范纪华) & Hong Shen  (谌 宏)

  3. School of Science, Nanjing University of Science and Technology, Nanjing, 210094, China

    Dingguo Zhang  (章定国)

Authors
  1. Jihua Fan  (范纪华)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dingguo Zhang  (章定国)
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hong Shen  (谌 宏)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dingguo Zhang  (章定国).

Additional information

Foundation item: the National Natural Science Foundation of China (Nos. 11502098 and 11772158), the Natural Science Foundation of the Higher Education Institutions of Jiangsu Province (No. 15KJB130003), the Doctoral Scientific Research Foundation of Jiangsu University of Science and Technology (No. 120140003), and the Fundamental Research Funds for Central Universities of China (No. 30917011103)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fan, J., Zhang, D. & Shen, H. Discretization Methods of a Rotating Flexible Rectangular Thin Plate. J. Shanghai Jiaotong Univ. (Sci.) 25, 118–126 (2020). https://doi.org/10.1007/s12204-019-2129-8

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12204-019-2129-8

Key words

CLC number

Document code

Search

Navigation