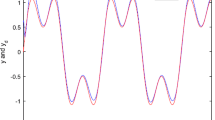Skip to main content
SpringerLink
Log in

Observer-based adaptive neural iterative learning control for a class of time-varying nonlinear systems

  • Published:
Journal of Shanghai Jiaotong University (Science) Aims and scope Submit manuscript

Abstract

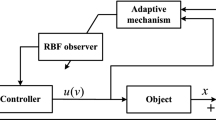
In this paper an adaptive iterative learning control scheme is presented for the output tracking of a class of nonlinear systems. An observer is designed to estimate the tracking errors. A mixed time domain and s-domain representation is constructed to derive an error model with relative degree one for our purpose. And time-varying radial basis function neural network is employed to deal with system uncertainty. A new signal is constructed by using a first-order filter, which removes the requirement of strict positive real (SPR) condition and identical initial condition of iterative learning control. Based on property of hyperbolic tangent function, the system tracing error is proved to converge to the origin as the iteration tends to infinity by constructing Lyapunov-like composite energy function, while keeping all the closed-loop signals bounded. Finally, a simulation example is presented to verify the effectiveness of the proposed approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. LEE H S, BIEN Z. A note on convergence property of iterative learning controller with respect to sup norm [J]. Automatica, 1997, 33(8): 1591–1593.

    Article  MathSciNet  MATH  Google Scholar 

  2. CHEN Y Q, GONG Z M, WEN C Y. Analysis of a high-order iterative learning control algorithm for uncertain nonlinear systems with state delays [J]. Automatica, 1998, 34(3): 345–353.

    Article  MathSciNet  MATH  Google Scholar 

  3. SUNM X, WANG DW. Iterative learning control with initial rectifying action [J]. Automatica, 2002, 38(7): 1177–1182.

    Article  MathSciNet  MATH  Google Scholar 

  4. CHIEN C J, LIU J S. A P-type iterative learning controller for robust output tracking of nonlinear timevarying systems [J]. International Journal of Control, 1996, 64(2): 319–334.

    Article  MathSciNet  MATH  Google Scholar 

  5. XU J X, TAN Y. A composite energy functionbased learning control approach for nonlinear systems with time-varying parametric uncertainties [J]. IEEE Transactions on Automatic Control, 2002, 47(11): 1940–1945.

    Article  MathSciNet  Google Scholar 

  6. XU J X, TAN Y, LEE T H. Iterative learning control design based on composite energy function with input saturation [J]. Automatica, 2004, 40(8): 1371–1377.

    Article  MathSciNet  MATH  Google Scholar 

  7. CHI R H, HOU Z S, XU J X. Adaptive ILC for a class of discrete-time systems with iteration-varying trajectory and random initial condition [J]. Automatica, 2008, 44(8): 2207–2213.

    Article  MathSciNet  MATH  Google Scholar 

  8. WANG Y C, CHIEN C J. Decentralized adaptive fuzzy neural iterative learning control for nonaffine nonlinear interconnected systems [J]. Asian Journal of Control, 2011, 13(1): 94–106.

    Article  MathSciNet  MATH  Google Scholar 

  9. XU J, XU J X. Iterative learning control for outputconstrained systems with both parametric and nonparametric uncertainties [J]. Automatica, 2013, 49(8): 2508–2516.

    Article  MathSciNet  Google Scholar 

  10. ZHANG C L, LI J M. Adaptive iterative learning control for nonlinear pure-feedback systems with initial state error based on fuzzy approximation [J]. Journal of the Franklin Institute, 2014, 351(3): 1483–1500.

    Article  MathSciNet  Google Scholar 

  11. LEU Y G, WANG W Y, LEE T T. Observer-based direct adaptive fuzzy-neural control for nonaffine nonlinear systems [J]. IEEE Transaction on Neural Networks, 2005, 16(4): 853–861.

    Article  Google Scholar 

  12. LIU Y J, ZHOU N. Observer-based adaptive fuzzyneural control for a class of uncertain nonlinear systems with unknown dead-zone input [J]. ISA Transactions, 2010, 49(4): 462–469.

    Article  Google Scholar 

  13. TONG S C, LI Y, LI Y M, et al. Observer-based adaptive fuzzy backstepping control for a class of stochastic nonlinear strict-feedback systems [J]. IEEE Transactions on Systems, Man, and Cybernetics. Part B: Cybernetics, 2011, 41(6): 1693–1704.

    Article  MathSciNet  Google Scholar 

  14. ZHOU B, LI Z Y, LIN Z L. Observer based output feedback control of linear systems with input and output delays [J]. Automatica, 2013, 49(7): 2039–2052.

    Article  MathSciNet  Google Scholar 

  15. DINH H T, KAMALAPURKAR R, BHASIN S, et al. Dynamic neural network-based robust observers for uncertain nonlinear systems [J]. Neural Networks, 2014, 60: 44–52.

    Article  MATH  Google Scholar 

  16. HUA C C, YU C X, GUAN X P. Neural network observer-based networked control for a class of nonlinear systems [J]. Neurocomputing, 2014, 133: 103–110.

    Article  Google Scholar 

  17. WANG Q D, WEI C L. Decentralized robust adaptive output feedback control of stochastic nonlinear interconnected systems with dynamic interactions [J]. Automatica, 2015, 54: 124–134.

    Article  MathSciNet  MATH  Google Scholar 

  18. CHEN B, LIN C, LIU X P, et al. Observer-based adaptive fuzzy control for a class of nonlinear delayed systems [J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2016, 46(1): 27–36.

    Article  Google Scholar 

  19. TAYEBI A, XU J X. Observer-based iterative learning control for a class of time-varying nonlinear systems [J]. IEEE Transactions on Circuits and Systems. I: Fundamental Theory and Applications, 2003, 50(3): 452–455.

    Article  MathSciNet  Google Scholar 

  20. XU J X, XU J. Observer based learning control for a class of nonlinear systems with time-varying parametric uncertainties [J]. IEEE Transactions on Automatic Control, 2004, 49(2): 275–281.

    Article  MathSciNet  Google Scholar 

  21. WANG Y C, CHIEN C J. An observer based adaptive iterative learning control for robotic systems [C]//2011 IEEE International Conference on Fuzzy Systems. Taipei: IEEE, 2011: 2876–2881.

    Chapter  Google Scholar 

  22. CHIEN C J, WANG Y C. An observer-based fuzzy neural network adaptive ILC for nonlinear systems [C]//13th International Conference on Control, Automation and Systems. Gwangju, Korea: IEEE, 2013: 226–232.

    Google Scholar 

  23. WANG Y C, CHIEN C J, ER M J. An observer-based adaptive iterative learning controller for MIMO nonlinear systems with delayed outputn [C]//13th International Conference on Control, Automation, Robotics and Visio. Singapore: IEEE, 2014: 157–162.

    Google Scholar 

  24. WANG Y C, CHIEN C J. An observer-based model reference adaptive iterative learning controller for MIMO nonlinear systems [C]//11th IEEE International Conference on Control & Automation (ICCA). Taipei: IEEE, 2014: 1168–1173.

    Chapter  Google Scholar 

  25. CHEN W S, LI R H, LI J. Observer-based adaptive iterative learning control for nonlinear systems with time-varying delays [J]. International Journal of Automation and Computing, 2010, 7(4): 438–446.

    Article  Google Scholar 

  26. GE S S, HANG C C, LEE T H, et al. Stable adaptive neural network control [M]. Norwell, USA: Kluwer Academic Publisher, 2001: 27–29.

    Google Scholar 

  27. POLYCARPOU M M. Stable adaptive neural control scheme for nonlinear systems [J]. IEEE Transactions on Automatic Control, 1996, 41(3): 447–451.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Control Engineering, Naval Aeronautical University, Yantai 264001, Shandong, China

    Jianming Wei  (韦建明)

  2. Department of Electrical and Electronic Engineering, Yantai Nanshan University, Yantai 265713, Shandong, China

    Youan Zhang  (张友安)

  3. Shandong Nanshan International Flight Co., Ltd., Yantai 265713, Shandong, China

    Jingmao Liu  (刘京茂)

Authors
  1. Jianming Wei  (韦建明)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Youan Zhang  (张友安)
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jingmao Liu  (刘京茂)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jianming Wei  (韦建明).

Additional information

Foundation item: the National Natural Science Foundation of China (No. 61273058)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wei, J., Zhang, Y. & Liu, J. Observer-based adaptive neural iterative learning control for a class of time-varying nonlinear systems. J. Shanghai Jiaotong Univ. (Sci.) 22, 303–312 (2017). https://doi.org/10.1007/s12204-017-1836-2

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12204-017-1836-2

Keywords

CLC number

Search

Navigation