Abstract
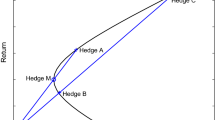
On the question of optimal hedge ratio, this paper firstly draws the chance to choose a market-entering point to the model. Using the replication principle of finance engineering, we make an assumed equity and get the optimal hedge ratio of the model, which gives the theoretical support to the practice. We should not only concern on the market-entering point, but also concern on the period of the hedge that still influences the effect of hedging. But only the period of hedging gives its affection if the time is relatively long.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
LU Y. Overseas “hedging” huge loss [J]. Manager, 2009(3): 86–87 (in Chinese).
HULL J. Hull options, futures, and other derivatives [M]. Beijing: Tsinghua University Press, 2006: 70–78.
LIU W, XIE C, CHEN D H. The optimal hedge ratio estimation method [J]. Comparative Economic and Social Systems, 2005(6): 71–74 (in Chinese).
PENG H F, YE Y G. The evaluation and comparison research of dynamic optimal hedging ratios based on modified ECM-GARCH [J]. Chinese Journal of Management Science, 2007, 15(5): 29–35 (in Chinese).
HE X B, ZHOU H. China’s futures market hedging effectiveness of measure [J]. Statistics and Decision, 2006(14): 56–58 (in Chinese).
YUAN X, YU S Q. Calculation of optimal hedge ratio of stock index futures under time-varying variance [J]. Journal of Dalian Maritime University (Social Science Edition), 2008, 7(1): 52–55 (in Chinese).
SHREVE E. Stochastic calculus for finance [M]. Shanghai: Shanghai University of Finance Press, 2008: 110–118.
YANG Q S, LIU H. An extension to moderate deviation for stochastic differential equation with poisson jumps and applications [J]. Acta Mathematica Sinica, 2009, 52(3): 601–604 (in Chinese).
XUE M G, ZHOU S B, HU S G. Stability of nonlinear neutral stochastic functional differential equations [J]. Journal of Applied Mathematics, 2010, 2010: 425762. 1–26.
CAMPELLO M, LIN C, MA Y, et al. The real and financial implications of corporate hedging [J]. The Journal of Finance, 2011, 66(5): 1616–1647.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhao, C., Bu, W. & Song, J. Price fluctuation, risk hedge and choice of optimal point. J. Shanghai Jiaotong Univ. (Sci.) 21, 51–56 (2016). https://doi.org/10.1007/s12204-016-1698-z
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12204-016-1698-z