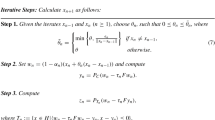Skip to main content
SpringerLink
Log in

An improved relaxed inertial projection algorithm for solving the minimum-norm solution of variational inequality and fixed point problems

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

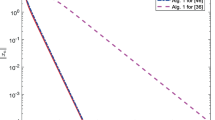
In this paper, a modified projection algorithm is proposed in order to solve a common element of the solution set of monotone variational inequality and the fixed point set of a class of quasi-pseudo-contractive mapping. This algorithm requires the monotonicity and Lipschitz continuity of the mapping, but don’t need to know Lipschitz constant. On one hand, this algorithm does not compute the projection onto the feasible set at each iteration, on the other hand, the strong convergence of the sequence generated by the algorithm can be obtained without viscosity technology, and the convergence rate of the algorithm better than some algorithms, and the effect of the algorithm is illustrated by two numerical experiments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Data availibility

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Code Availability

The Code that support the findings of this study are available from the corresponding author upon reasonable request.

References

  1. Korpelevic, G.M.: The extragradient method for finding saddle points and other problems. Ekon. Mat. Metody. 12, 747–756 (1976)

    MathSciNet  Google Scholar 

  2. Tseng, P.: A modified forward-backward splitting method for maximal monotone mappings. SIAM J. Control. Optim. 38, 431–446 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  3. Censor, Y., Gibali, A., Reich, S.: The subgradient extragradient method for solving variational inequalities in Hilbert space. J. Optim. Theory Appl. 148, 318–335 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  4. Censor, Y., Gibali, A., Reich, S.: Extensions of Korpelevichs extragradient method for the variational inequality problem in Euclidean space. Optimization 61, 1119–1132 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  5. Vuong, P.T., Vinh, L.V.: Convergence rate of a gradient projection method for solving variational inequalities. J. Nonlinear Var. Anal. 5, 951–964 (2021)

    MATH  Google Scholar 

  6. Bauschke, H.H., Phan, H.M., Noll, D.: Linear and strong convergence of algorithms involving averaged nonexpansive operators. J. Math. Anal. Appl. 421, 1–20 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  7. Solodov, M.V.: Convergence rate analysis of iteractive algorithms for solving variational inequality problems. Math. Program. 96, 513–528 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  8. Badea, L., Tai, X.C., Wang, J.: Convergence rate analysis of a multiplicative Schwarz method for variational inequalities. SIAM J. Numer. Anal. 41, 1052–1073 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  9. Polyak, B.T.: Some methods of speeding up the convergence of iterates methods. USSR Comput. Math. Phys. 4, 1–17 (1964)

    Article  Google Scholar 

  10. Nesterov, Y.: A method of solving a convex programming problem with convergence rate O(1/k2). Soviet Math. Doklady. 27, 372–376 (1983)

    MATH  Google Scholar 

  11. Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2, 183–202 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  12. Alakoya, T.O., Owolabi, A.O.E., Mewomo, O.T.: An inertial algorithm with a self-adaptive step size for a split equilibrium problem and a fixed point problem of an infinite family of strict pseudo-contractions. J. Nonlinear Var. Anal. 5, 803–829 (2021)

    Google Scholar 

  13. Ogwo, G.N., Alakoya, T.O., Mewomo, O.T.: Inertial forward-backward method with self-adaptive step sizes for finding minimum-norm solutions of inclusion and split equilibrium problems. Appl. Set-Valued Anal. Optim. 4, 185–206 (2022)

    Google Scholar 

  14. Godwin, E.C., Izuchukwu, C., Mewomo, O.T.: An inertial extrapolation method for solving generalized split feasibility problems in real Hilbert spaces. Boll. Unione Mat. Ital. 14, 379–401 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  15. Yao, Y., Iyiola, O.S., Shehu, Y.: Subgradient extragradient method with double inertial steps for variational inequalities. J. Sci. Comput. 90, 1–29 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  16. Gibali, A., Shehu, Y.: An efficient iterative method for finding common fixed point and variational inequalities in Hilbert spaces. Optimization 68, 13–32 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  17. Shehu, Y., Ogbuisi, F.U.: An iterative algorithm for approximating a solution of split common fixed point problem for demi-contractive maps. Dyn. Contin. Discrete Impuls. Syst. Ser. B Appl. Algorithms 23, 205–216 (2016)

    MathSciNet  MATH  Google Scholar 

  18. Shehu, Y., Cholamjiak, P.: Iterative method with inertial for variational inequalities in Hilbert spaces. Calcolo 56, 1–21 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  19. Yao, Y., Postolache, M.: Iterative methods for pseudomonotone variational inequalities and fixed point problems. J. Optim. Theory Appl. 155, 273–287 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  20. Yao, Y., Shahzad, N., Yao, J.C.: Convergence of Tseng-type self-adaptive algorithms for variational inequalities and fixed point problems. Carpathian J. Math. 37, 541–550 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  21. Zhao, X., Yao, Y.: Modified extragradient algorithms for solving monotone variational inequalities and fixed point problems. Optimization 69, 1987–2002 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  22. Tan, B., Zhou, Z., Li, S.: Viscosity-type inertial extragradient algorithms for solving variational inequality problems and fixed point problems. J. Appl. Math. Comput. 68, 1387–1411 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  23. Linh, H.M., Reich, S., Thong, D.V.: Analysis of two variants of an inertial projection algorithm for finding the minimum-norm solutions of variational inequality and fixed point problems. Numer. Algorithms 89, 1695–1721 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  24. Zhou, H., Qin, X.: Fixed Points of Nonlinear Operators. De Gruyter, Berlin (2020)

    Book  MATH  Google Scholar 

  25. Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer, New York (2017)

    Book  MATH  Google Scholar 

  26. Chang, S., Wang, L., Qin, L.J.: Split equality fixed point problem for quasi-pseudo-contractive mappings with applications. Fixed Point Theory Appl. 1, 1–12 (2015)

    MathSciNet  MATH  Google Scholar 

  27. He, S., Xu, H.K.: Uniqueness of supporting hyperplanes and an alternative to solutions of variational inequalities. J. Global Optim. 57, 1375–1384 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  28. Tan, K.K., Xu, H.K.: Approximating fixed points of nonexpansive mappings by the Ishikawa iteration process. J. Math. Anal. Appl. 178, 301–308 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  29. Saejung, S.S., Yotkaew, P.: Approximation of zeros of inverse strongly monotone operators in Banach spaces. Nonlinear Anal. 75, 742–750 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  30. Godwin, E.C., Alakoya, T.O., Mewomo, O.T.: Relaxed inertial Tseng extragradient method for variational inequality and fixed point problems. Appl. Anal. 2022, 1–26 (2022)

    Article  Google Scholar 

  31. Alakoya, T.O., Jolaoso, L.O., Mewomo, O.T.: Modified inertial subgradient extragradient method with self adaptive stepsize for solving monotone variational inequality and fixed point problems. Optimization 70, 545–574 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  32. Thong, D.V., Hieu, D.V.: Some extragradient-viscosity algorithms for solving variational inequality problems and fixed point problems. Numer. Algorithms 82, 761–789 (2019)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

This research was funded by National Natural Science Foundation of China (Grant No. 11872043), Natural Science Foundation of Sichuan Province (Grant No. 2023NSFSC1299), Fund Project of Sichuan University of Science and Engineering in hit-haunting for talents (Grant No. 2022RC04), 2021 Innovation and Entrepreneurship Training Program for College Students of Sichuan University of Science and Engineering (Grant No. cx2021150), 2022 Graduate Innovation Project of Sichuan University of Science and Engineering (Grant No. Y2022190).

Author information

Authors and Affiliations

  1. College of Mathematics and Statistics, Sichuan University of Science and Engineering, Zigong, 643000, Sichuan, China

    Huan Zhang, Xiaolan Liu, Jia Deng & Yan Sun

  2. South Sichuan Center for Applied Mathematics, Zigong, 643000, Sichuan, China

    Xiaolan Liu

  3. Artificial Intelligence Key Laboratory of Sichuan Province, Zigong, 643000, Sichuan, China

    Xiaolan Liu

Authors
  1. Huan Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaolan Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jia Deng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yan Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Conceptualisation of the article and methodology were given by HZ; formal analysis, investigation, and writing-original draft preparation by HZ and JD; software and validation by HZ and XLL, writing-review and editing by HZ, YS, and JD. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Xiaolan Liu.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Ethical approval

Not applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, H., Liu, X., Deng, J. et al. An improved relaxed inertial projection algorithm for solving the minimum-norm solution of variational inequality and fixed point problems. J. Appl. Math. Comput. 69, 2717–2739 (2023). https://doi.org/10.1007/s12190-023-01853-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-023-01853-z

Keywords

Mathematical Subject Classification

Search

Navigation