1 Introduction

A classical reaction-diffusion equation (RDE) arises in many areas of sciences and engineering, such as chemistry [1], pattern formation [2, 3], ecological invasions [4], spread of epidemics [5], biophysics [6, 7], and many other areas [8,9,10]. In general, an RDE represents a mathematical model where several components interact. In ecology, a classical RDE model plays an important role in studying different types of species dynamics [10].

The biological diversity of the earth is affected by habitat loss and fragmentation. Understanding the consequences of these effects on the persistence of native populations and communities is one of the challenging problems in conservation biology. Interactions of two species may be altered due to habitat loss and fragmentation, which illustrates the critical links between spatial ecology and conservation [11]. For instance, during an avian influenza outbreak, different culling strategies could be incorporated as a control measure to minimize the long-term effects on genetic diversity [12]. Environmental factors do not only affect to the biological diversity but they influence human diseases too. Eco-epidemiological models are used to investigate the transmission dynamics of an infectious disease engaged with a prey-predator connection in the impact of sickness in ecological models [13,14,15]. A model consists of a four-dimensional system of differential equations is considered to study the global dynamics for a honeybee colony infested by virus-carrying Varroa mites in [16].

In theoretical ecology, the determination of distribution (density) of species (or organisms) and the structure of communities is one of the main goals where species (or organisms) interact with each other in a given environment [17]. In the recent decade, the role of spatial effects in preserving biodiversity has received a great deal of attention in the literature on conservation [18,19,20,21].

There is a substantial difference between classical and directed diffusion. For instance, in classical diffusion some movements are unpredictable; whereas a directed diffusion focuses on selecting habitat influences. Populations differ in the diffusion strategies they employ as well as in their environmental intensities [22,23,24]. Further, the competition between populations also has influences on the diffusion [25,26,27].

Both autonomous and non-autonomous population models subject to either impulsive or continuous harvesting were studied in [28, 29] and found that the impulsive strategy can be as good as the continuous one but cannot outperform. The effect of periodic habitat fluctuations on a nonlinear insect population model has been studied in [30] and illustrate the possibility of a significant increase in population numbers using both theorically and experimentally. The harvesting problem in the seasonal environment was considered in [31], presented a general harvesting model with seasonal carrying capacity and developed a theoretical foundation. A diffusive predator-prey models are analyzed and studied in [32, 33], complex dynamics of these models are visualized in the presence of the predator harvesting. A density-dependent prey-predator model having the effect of harvesting is investigated in [34]. Moreover, prey-predator population model with fear and Allee effects is considered in [35]. This paper investigates the global existence of the solution of a diffusive directed dynamic (DDD) model, which is a variant of the classical RDE model. In the proposed DDD model, we consider the resource distribution is uniform per capita according to the distribution function with the homogeneous Neumann boundary condition which is interpreted as there is no flux of population on the boundary; or the number of populations that come in and go out at each point on the boundary is equal at each moment, so the total number of populations is in balance. In addition, we incorporate the harvesting effect in the DDD model and study its dynamics.

In the present DDD model, we consider a dispersed function-driven diffusion when species migrate to its favorable environment, not just the carrying capacity. Note that the desired environment of any species can be equivalent to the carrying capacity, but the converse is not true [36]. There can be any partition of carrying capacity where the resource for any population is high. Thus, species move to that location from where it exists. The stability of solutions of the equation with the logistic type of growth was first studied in [37] and then extended in [38] with general growth function. The influence of harvesting for a two-species competition was studied in [39] with a spatially heterogeneous environment. In this paper, we consider the time and space involving disperse diffusion.

One important observation is how diffusion terms are added to an RDE or a DDD model. Commonly, in a regular diffusion, it takes the form \(d\Delta v (t, x)\), where d is the specific diffusion rate and v(t, x) is the density of the species at time t and position x. In the case of directed diffusion, carrying capacity-driven diffusion is an important term, and has the form \(d\Delta \left( \frac{v(t, x)}{K(t, x)}\right) \), where K(t, x) is the carrying capacity of the environment. In this paper we incorporated the new directed diffusion term, \(d\Delta \left( \frac{v(t,x)}{P(t,x)}\right) \), known as the disperse diffusion, where P(t, x) is some positive and bounded resource distribution function. Both K, and P have the same dimension as v.

Many organisms, which follow this type of diffusion strategy, compete for common land, food habitat, etc., slow each other’s growth rate and diffuse according to the properties of the common space they need. For instance, like deers, they tend to move toward green areas for the food chain. If a forest area is in-habitat, they move to other spaces or become extinct. This study explores a population distribution that has a tremendous application in different areas of ecology and economy; instantaneous examples are in river and ocean ecology to observe the seasonal behaviors of different species, including wild animals and winter birds. We investigate global well-posedness of the mathematical model, determine conditions on harvesting rate for which non-trivial equilibrium states exist and examine their global stability for both spatial and time dependent periodic functions with the same period. For time periodic growth, resource, capacity and harvesting functions, we prove the existence of time-periodic states.

The main objectives of the study are: (1) We will study with an influencing diffusion model where the resource distribution is uniform per capita instead of random to observe that the coherent strategy is favorable for the species in competition. (2) It is expected that any species’ movement (diffusion) according to the distribution function changes the persistence and extinction threshold. (3) Including the new diffusion strategy in the model leads the species to be depending on the resource distribution function, which governs the environmental carrying capacity. (4) In addition, theory does not give any idea about the profile of nonzero equilibrium state \(v_s\), except when resource function P is proportional to the capacity function K. We have explored this numerically since it is important from ecological considerations.

The rest of the paper is organized as follows: In Sect. 2, the DDD model is developed. In Sect. 3, the existence and uniqueness of solution of a DDD model is presented along with a convergence analysis. In Sect. 4, we present the proof of the existence of time-periodic solution in a bounded region. The dynamics of harvesting and its applications are being described in Sect. 5. Some examples are presented in Sect. 6 for applications. Finally, Sect. 7 concludes the summary and discussion of the results.

2 Mathematical model

To investigate the spatial effects in ecology, the random RDE models are well established and used widely (see [1]–[6]). These models support the following three important types of ecological phenomena: (1) A minimal patch size is needed to sustain a population and its growth, (2) Biological invasions generate the propagation of wavefronts, and (3) The spatial patterns are formed in the distributions of populations in homogeneous environments. By observing the classical diffusion model, in this paper, we consider the following DDD system to model the density of the species v(t, x):

$$\begin{aligned} \frac{\partial v}{\partial t} =&\,\, d\Delta \left( \frac{v}{P} \right) + rv\left( 1-\frac{v}{K} \right) -Y_h v, \; (t,x) \in \Gamma , \end{aligned}$$
(1)
$$\begin{aligned} \nabla \left( \frac{v}{P} \right) \cdot n=&\,\, 0, \; (t,x) \in {\partial \Gamma }, \end{aligned}$$
(2)
$$\begin{aligned} v(0,x)=&\,\, v_0(x), \;x\in {\Omega }, \end{aligned}$$
(3)

where \(\Omega \subset \mathbb {R}^N\) is an open domain, \(N\in \{1, 2, 3\}\), n is the outward normal vector to the boundary. P(t, x) is a resource distribution function, K(t, x) is the carrying capacity of the environment, r(t, x) is the specific growth rate, \(Y_h(t,x)\) is the harvesting function, \(v_0\) is the initial density of the species, \(\Gamma =(0,T] \times \Omega , \; \partial \Gamma =(0,T] \times \partial \Omega \) for any \(T>0\), and \(\Gamma _{\infty }=(0, \infty ) \times \Omega \). In this model, the distribution function ensures the resource is uniformly distributed per capita, also the population is assumed to be distributed according to the available per resource. The modified diffusion term leads to the homogeneous Neumann boundary condition, and was first introduced in [18] motivated by the choice of optimal harvesting strategies. This alternative model of time-dependent spatial reaction-diffusion equation to study the population distribution in a heterogeneous environment, where diffusive transport of population is proportional to the gradient of population density per unit capacity instead of just the population density. In this model, populations are distributed based on available resources. It is an influencing diffusion model where the resource distribution is uniform per capita to observe that the coherent strategy is favorable for the species in competition. Other nonlinear diffusion types, based on the experimental data, were considered in population dynamics [40,41,42].

Remark 1

The functions P, K, and r are all depend on both t, and x, unless otherwise state.

Throughout this paper, we assume \(P>0\) in \(\overline{\Gamma }\), \(P \in {C^{1+\alpha /2, 2+ \alpha }(\overline{\Gamma }_{\infty })}\) for some \(\alpha \in {(0,1)}\) and functions P, \(\frac{\partial P}{\partial t}\), K, and \(\frac{\partial K}{\partial t}\) are uniformly bounded from below and above in \(\overline{\Gamma }\).

The equilibrium point of the above system is \(v^*(x)\), where \(v^*=0\) is the obvious as a trivial steady-state. Our primary interest is non-trivial equilibrium. In absence of harvesting (\(Y_h\equiv 0\)), all possible equilibrium points of the above system can be obtained as either for \(\frac{K(x)}{P(x)}\equiv k\) or \(\frac{K(x)}{P(x)}\not \equiv k,\) where k is a constant. If \(P(x)=K(x)\), then \(v^*(x)=K=P\) is the only non-trivial equilibrium point. If the resource function and capacity function are not proportional then \(v^*(x)\) is the non-trivial steady-state. For non-zero harvesting (\(Y_h\not \equiv 0\)), \(v^*(x)\) is the unique steady-state neither K(x) nor P(x). It is also noted that when diffusion coefficient is small, equilibrium state \(v^*(x) \approx K(x)\), whereas when diffusion effects are large, \(v^*(x)\) is proportional to P(x) as presented numerically.

We define \(g(t,x,v):=r\big (1-\frac{ v}{K}\big )\), and \(h(t,x,v):=vg\) and have the following assumptions:

  1. (h1)

    h is uniformly Hölder continuous in \(\overline{\Gamma } \times J\), where J is either a suitable sub-interval of \(\mathbb {R}\) or a sector between lower and upper solutions. Moreover, functions h and \(\frac{\partial f}{\partial v}\) are \(C^1([0,T])\) as functions of t, Hölder continuous in \(\overline{\Omega }\) in the x variable and continuous in \(\mathbb {R}\) as functions of v.

  2. (h2)

    g(t, x, v) is strictly monotonically decreasing in v, \(g(t,x,v)<0\) when \(v>K\), and \(g(t,x,v)>0\) when \(0<v<K\), for \((t,x) \in {\Gamma }\).

  3. (h3)

    \(g(t,x, \cdot ) \in {C^2 (\mathbb {R})}\).

It is easy to verify that the logistic growth function with positive bounded r follows the above (h1)–(h3) assumptions. In the following sections, for establishing several results, we assume the conditions (h1)-(h3) hold.

3 Existence, uniqueness, and convergence analysis

For convenience, everywhere in this section, we assume

  1. (i)

    P and K are Hölder continuous in x and continuously differentiable periodic function, \(K>0\) for any \((t,x) \in { \overline{\Gamma }}\),

  2. (ii)

    r is continuous in \(\Gamma _{\infty }\), periodic and \(r>0\) for any \((t,x) \in {\overline{\Gamma }}\).

The domain \(\Omega \) is nonempty open bounded with \(\partial \Omega \in {C^{\alpha +1}},\; 0< \alpha <1\). We first state and proof the existence and uniqueness theorem for the time dependent distribution function, carrying capacity, and specific growth rate.

Theorem 1

Let the initial function \(v_0(x) \in {C(\Omega )}\), \(v_0(x)>0\), and \(Y_h(t,x)\equiv 0\) in a nonempty open bounded sub-domain \(\Omega _s \subset \Omega \). Then there exists a unique attractor v of the problem (1)-(3) and the solution is positive.

Proof

For simplicity and to translate the diffusion term in classical style, we first make the following substitution

$$\begin{aligned} w(t,x):= \frac{v}{P}, \end{aligned}$$

and since the function P is positive and bounded from above in \(\overline{\Gamma }\), the new variable w is well defined. We obtain that function w satisfies

$$\begin{aligned} \frac{\partial w}{\partial t}+ \frac{w}{P} \frac{\partial P}{\partial t}- \frac{d}{P} \Delta w = rw \left( 1- \frac{Pw}{K} \right) . \end{aligned}$$

Then the equivalent system of (1)-(3) is

$$\begin{aligned} \frac{\partial w}{\partial t}+ \frac{ w}{P} \frac{\partial P}{\partial t}- \frac{ d}{P} \Delta w&= rw \left( 1- Hw \right) , \; (t,x)\in {\Gamma }, \end{aligned}$$
(4)
$$\begin{aligned} \frac{\partial w}{\partial n}&=0,\; (t,x) \in {\partial \Gamma }, \end{aligned}$$
(5)
$$\begin{aligned} w(0,x)&=\frac{ v(0,x)}{P(0,x)},\; x\in {\Omega }, \end{aligned}$$
(6)

where we define

$$\begin{aligned} H=\sup \limits _{(t,x) \in {\Gamma }} \frac{ P(t,x)}{ K(t,x)}. \end{aligned}$$
(7)

For some particular functions in the domain, either K is proportional to P or they are non-proportional. It is obvious that the operator \(\mathcal {L}:=d^*(t,x)\Delta \) is uniformly elliptic with the coefficient \(d^*:=d/P\) that is Hölder continuous. Therefore, according to Lemma A2, to show that the existence of the unique solution of (4)-(6), we only need to construct an ordered pair of upper and lower solutions. To construct an upper solution, denote

$$\begin{aligned} \beta (t,x):= \frac{1}{P} \frac{\partial P}{\partial t}, \end{aligned}$$
(8)

and consider a constant C such that

$$\begin{aligned} C \ge \sup \limits _{(t,x)\in {\Gamma _{\infty }}} \frac{v_0(x)}{P(t,x)} \ge \sup \limits _{(t,x)\in {\Gamma }} \frac{v_0(x)}{P(t,x)}, \end{aligned}$$
(9)

and \(r(1-H C) <0\) which can be found according to (h2). Note that since \(v_0\) is bounded in \(\overline{\Gamma }\) and K is bounded from below,

$$\begin{aligned} \sup _{(t,x)\in {\Gamma }} \frac{v_0(x)}{P(t,x)} < \infty . \end{aligned}$$

Next, choose

$$\begin{aligned} \gamma \ge \sup _{(t,x)\in {\Gamma }} |\beta (t,x)| \end{aligned}$$

and let \(w^*(t,x) \equiv Ce^{\gamma t}\). Then

$$\begin{aligned} \frac{\partial w^*}{\partial t}- \frac{d}{P} \Delta w^*= \gamma w^*, \end{aligned}$$

gives

$$\begin{aligned} w^* \left( r- r H w^*- \beta \right) \le \gamma w^*, \end{aligned}$$
(10)

for some particular bounded functions P, and K if condition (7) holds. Thus, the first inequality of (57) in Definition A2 holds. Further,

$$\begin{aligned} \frac{\partial w^*}{\partial n} =0 \; \text {and} \; w^* \ge w(0,x). \end{aligned}$$

Therefore, \(w^*\) is an upper solution of (4)-(6) by Definition A2. The function \(w_*(t,x) \equiv 0\) is obviously a lower solution. Check that the right-hand side of the following function

$$\begin{aligned} l(t,x,w,K,P):= rw \left( 1- \frac{P}{K} w \right) - \beta w \end{aligned}$$

is continuously differentiable with respect to w and we can denote the maximal derivative of l in w for each (t, x)

$$\begin{aligned} g_*(t,x)&= \sup \left\{ -l_w(t,x,w,K,P), w_* \le w \le w^* \right\} ,\\ g^*(t,x)&= \sup \left\{ l_w(t,x,w,K,P), w_* \le w \le w^* \right\} . \end{aligned}$$

Then, the Lipschitz condition (59) holds and by Lemma A2, there exists a unique solution of the problem (4)-(6) satisfying \(w_*\le w\le w^*\). Finally, using the inverse substitution we obtain a unique solution of (1)-(3).

To ensure that the solution is positive for any non-negative initial function \(v_0(x)\), we assume

$$\begin{aligned} s(t,x)=w e^{At} = \frac{v}{P}e^{At}, \end{aligned}$$

where

$$\begin{aligned} A:= w^* \sup _{(t,x) \in {\overline{\Gamma }}} \left[ r(t,x)H \right] + \sup _{(t,x) \in {\overline{\Gamma }}} |\beta (t,x)|. \end{aligned}$$

The inverse substitution, \(w=s e^{-At}\) into (4)-(6), we have

$$\begin{aligned} \frac{\partial s}{\partial t} - \frac{d}{P} \Delta s =&\left[ rw \left( 1- \frac{P}{K}w\right) -\beta w+ Aw \right] e^{At} \ge 0, (t,x) \in {\overline{\Gamma }}, \end{aligned}$$
(11)
$$\begin{aligned} \frac{\displaystyle \partial s}{\displaystyle \partial n}=&0, (t,x) \in {\partial \overline{\Gamma }}, \end{aligned}$$
(12)
$$\begin{aligned} s(0,x)=&w(0,x)\ge 0, \; x\in {\Omega }. \end{aligned}$$
(13)

To study (11)-(13), note that s is non-negative since \(w\ge w_*=0\). Then, assume that s has a zero at some point \( (t_0,x_0) \). If \((t_0,x_0) \in {\Gamma }\) then according to the maximum principle, we obtain \(s(t,x) \equiv 0\) in \(\Gamma \), for details, see Lemma A3. According to the assumption of the theorem \(s(0,x)>0\) on some open bounded sub-domain \(\Omega _s \subset \Omega \) and \(s\in {C(\overline{\Gamma })} \) since w is a solution of (4)-(6). Therefore \(s(t,x)>0\) in \(\Gamma \). Moreover, if \(s(t_1,x_1)=0\) for some \((t_1,x_1) \in {\partial \Gamma }\) then by Lemma A2, we have \(\frac{\partial s}{\partial n}<0\) at \((t_1,x_1)\) which contradicts the no flux boundary conditions in (11)-(13). This concludes the proof. \(\square \)

Now we consider the system (1)-(3) without harvesting and with spatially distributed parameters P(x), K(x), and r(x):

$$\begin{aligned} \frac{\partial v}{\partial t}=&\, d \Delta \left( \frac{v}{P(x)} \right) + r(x)v \left( 1- \frac{v}{K(x)} \right) , \; (t,x)\in {\Gamma }, \end{aligned}$$
(14)
$$\begin{aligned} \nabla \left( \frac{ v}{P(x)} \right) \cdot n=&\, 0, \; (t,x) \in {\partial \Gamma }, \end{aligned}$$
(15)
$$\begin{aligned} v(0,x)=&\, v_0(x),\; x \in { \Omega }. \end{aligned}$$
(16)

The result of Theorem 1 will apparently valid for (14)-(16). The next result shows that when the carrying capacity and the intrinsic growth rate are only distributed spatially, and \(P(x)\equiv K(x)\) then \(v(x):\equiv K(x)\equiv P(x)\) is an equilibrium solution of (14)-(16). Also, the solution v(t, x) of (1)-(3) with \(Y_h(t,x)\equiv 0\) converges to K(x) for any \(v_0(x) \ge 0, \; v_0(x) \not \equiv 0\) [37], with the following estimated convergence speed

$$\begin{aligned} \int \limits _{\Omega } |v(t,x)-K(x)|dx \le e^{-\inf _{\Omega } r(x) t} \int \limits _{\Omega } K(x)\;dx. \end{aligned}$$

We now consider the arbitrary distribution function, P(x) and carrying capacity, K(x), and we have the following result.

Theorem 2

If the rational function \(\frac{\displaystyle K(x)}{\displaystyle P(x)} \not \equiv k\), where k is a constant then \(v^*(x)\) is an equilibrium solution of (14)-(16). Moreover, for any \(v_0(x) \ge 0, \; v_0(x) \not \equiv 0\) the solution v(t, x) of (1)-(3) with \(Y_h(t,x)\equiv 0\) converges to \(v^*(x)\), with the estimated convergence speed as

$$\begin{aligned} \int _{\Omega } |v(t,x)-v^*(x)|dx \le Ce^{-\Upsilon t}, {\text {where}\Upsilon = \inf _{\Omega } r(x)>0.} \end{aligned}$$
(17)

Proof

Define the constants

$$\begin{aligned} M^*:= \max \left\{ \sup \limits _{x\in {\overline{\Omega }}} v(0,x),\; \sup \limits _{x\in {\overline{\Omega }}} v^*(x)\right\} ,\text {and} m^*:= \min \left\{ \inf \limits _{x\in {\overline{\Omega }}} v(T,x),\; \inf \limits _{x\in {\overline{\Omega }}} v^*(x)\right\} , \end{aligned}$$

for some fixed moment \(T>0\). Note that \(m^*>0\) since \(v^*(x)>0\) by assumption and \(v(T,x)>0\) for any \(x\in {\overline{\Omega }}, \; T>0\) by Theorem 1.

Let \(v_{M^*}(t,x)\) and \(v_{m^*}(t,x)\) be the solutions of (14)-(16) satisfying initial conditions \(v_{M^*}(0,x)=M^* \ge v_0(x)\) and \(v_{m^*}(T,x)= m^* \le v(T,x)\), respectively. According to Definition A2 the function \(v_{M^*}(t,x)\) satisfies (57) and it is an upper solution of (14)-(16). The function \(v_{m^*}(t,x)\) is a lower solution of the problem (14)-(16) with the initial condition at the moment T which is v(T, x). Then, by Theorem 1 we have \(v_{M^*}(t,x) \ge v(t,x)\) and \(v(t,x) \le v_{m^*}(t,x)\) for any \(t \ge T\) such that

$$\begin{aligned} v_{m^*}\le v \le v_{M^*}\; \text {for any}\; (t,x)\in {[T, \infty ) \times \Omega .} \end{aligned}$$

Thus, for any positive \(v^*(x)\), the above inequalities imply

$$\begin{aligned}&v_{m^*}(t,x)-v^*(x) \le v(t,x)-v^*(x) \le v_{M^*}(t,x)-v^*(x)\; \text {for any}\nonumber \\&(t,x)\in {[T, \infty ) \times \Omega }. \end{aligned}$$
(18)

The following two inequalities are deduced from the same idea as above and hence

$$\begin{aligned} v_{m^*}(t,x)-v^*(x) \le 0,\; v_{M^*}(t,x)-v^*(x) \ge 0, (t,x)\in {[T, \infty ) \times \Omega }. \end{aligned}$$
(19)

Combining (18) and (19) leads to

$$\begin{aligned}&|v(t,x)-v^*(x)| \le \max \{v_{M^*}(t,x)-v^*(x),v^*(x)-v_{M^*}(t,x) \},\; (t,x)\\&\quad \in {[T, \infty ) \times \Omega }. \end{aligned}$$

Thus, integrating both sides yields.

$$\begin{aligned}&\int \limits _{\Omega } |v(t,x)-v^*(x)| dx \nonumber \\&\quad \le \max \left\{ \int \limits _{\Omega } (v_{M^*}(t,x)-v^*(x))\; dx, \int \limits _{\Omega } (v^*(x)-v_{m^*}(t,x))\;dx \right\} . \end{aligned}$$
(20)

We now define \(z(t,x):=v_{M^*}(t,x)-v^*(x)\) and then \(z\ge 0\) by (19) and substituting in (14)-(16), we have

$$\begin{aligned} \begin{aligned}&\frac{\partial z}{\partial t} = d \Delta \left( \frac{z(t,x)}{P(x)} \right) + d \Delta \left( \frac{v^*(x)}{P(x)} \right) +\frac{r(x)}{K(x)}v_{M^*}(t,x)(K-v_{M^*}(t,x)). \end{aligned} \end{aligned}$$
(21)

Integrating both sides of (21) over \(\Omega \) and using the Neumann boundary conditions with the application of the Gauss theorem yields

$$\begin{aligned} \frac{d}{dt} \int \limits _{\Omega } z(t,x)\;dx=d \nabla \left( \frac{v^*(x)}{P(x)} \right) + \int \limits _{\Omega } \frac{r(x)}{K(x)}v_{M^*}(K-v_{M^*})\; dx. \end{aligned}$$
(22)

Since \(v_{M^*}\) is an upper solution of (14)-(16), we have

$$\begin{aligned} \begin{aligned}&d \Delta \left( \frac{v_{M^*}}{P} \right) + \frac{r(x)}{K(x)}v_{M^*}\left( K(x)- v_{M^*} \right) \le 0, \text {which yields}\\&\frac{r(x)}{K(x)}v_{M^*} \left( v_{M^*}-K(x) \right) \ge \;d \Delta \left( \frac{v_{M^*}}{P} \right) . \end{aligned} \end{aligned}$$

Integrating over the domain, using boundary conditions, and \(\nabla \left( \frac{v_{M^*}}{P} \right) \ge 0\) we get

$$\begin{aligned} \int \limits _{\Omega } \frac{r(x)}{K(x)}v_{M^*} \left( v_{M^*}-K(x) \right) \; dx \ge 0. \end{aligned}$$
(23)

Since \(K(x) \not \equiv P(x)\), for a real constant \(\alpha >0\), it is possible to write \(K(x)=P(x) + \alpha \) and the gradient, \(\nabla \left( \frac{v^*(x)}{P(x)} \right) \) will no longer be zero. Then for some \(v^*(x)\) and P(x), \(\nabla \left( \frac{v^*(x)}{P(x)} \right) \le 0\) which yields the following inequalities from (22) and we have

$$\begin{aligned} \begin{aligned} \frac{d}{dt} \int \limits _{\Omega } z(t,x)\;dx&\le -\int \limits _{\Omega } \frac{r(x)}{K(x)} v_{M^*} (v_{M^*}-K(x))\; dx\\&= - \int \limits _{\Omega } \frac{r(x)}{K(x)} z (v_{M^*}-K(x))\; dx -\int \limits _{\Omega } \frac{r(x)}{K(x)} v^* (v_{M^*}-K(x))\;dx\\&\le - \int \limits _{\Omega } \frac{r(x)}{K(x)} z (v_{M^*}-K(x))\; dx \\&\le - \int \limits _{\Omega } r(x) z(t,x)\; dx \le - \Upsilon \int \limits _{\Omega } z(t,x)\; dx. \end{aligned} \end{aligned}$$

Therefore by using Grönwall’s lemma A4, we get

$$\begin{aligned} \int \limits _{\Omega } z(t,x)\;dx \le e^{-\Upsilon t}\int \limits _{\Omega } z(0,x)\; dx \le e^{-\Upsilon t}\int \limits _{\Omega } (M^*-v^*(x)) \; dx, \end{aligned}$$

which implies

$$\begin{aligned} \int \limits _{\Omega } (v_{M^*}(t,x)-v^*(x)) \; dx \le e^{-\Upsilon t}\int \limits _{\Omega } (M^*-v^*(x)) \; dx. \end{aligned}$$
(24)

While we consider the lower solution, \(v_{m^*}(t,x)\), similarly, it is easy to establish the following integrals relation.

$$\begin{aligned} \int \limits _{\Omega } (v^*(x)-v_{m^*}(t,x)) \; dx \le e^{-\Upsilon t}\int \limits _{\Omega } (v^*(x)-m^*) \; dx. \end{aligned}$$
(25)

Finally from (20), (24), and (25) it follows that

$$\begin{aligned} \int \limits _{\Omega } |v(t,x)-v^*(x)|dx \le C e^{-\Upsilon t} , \;\text {for any} \; t\in {[T, \infty )}, \end{aligned}$$

where

$$\begin{aligned} C \equiv \max \left\{ \int \limits _{\Omega } (M^*-v^*(x))\; dx, \int \limits _{\Omega } (v^*(x)-m^*)\; dx \right\} .\end{aligned}$$

If t is too large and tends to \(\infty \) then

$$\begin{aligned} \lim \limits _{t \rightarrow \infty } \int \limits _{\Omega } |v(t,x)-v^*(x)|dx=0, \end{aligned}$$
(26)

for any non-negative and not identically zero initial value \(v_0(x)\) in \(\Omega \). Equality (26) implies the uniqueness of the positive equilibrium solution. \(\square \)

For rational functions, all non-negative and non-trivial solutions converge to the positive steady-state K(x), and we can estimate the convergence rate. The result is prescribing in the following Theorem.

Theorem 3

If the function \(K(x) \equiv \alpha P(x),\;\alpha >0\) in (14)-(16) then for any \(v_0(x) \ge 0, \; v_0(x) \not \equiv 0\) the solution v(t, x) of (1)-(3) with \(Y_h(t,x)\equiv 0\) converges to K(x), with the convergence speed estimated as

$$\begin{aligned} \int \limits _{\Omega } |v(t,x)-K(x)|dx \le \alpha e^{-\Upsilon t} \int \limits _{\Omega } P(x)\;dx. \end{aligned}$$

As far as the function K(x) and P(x) are rational, the proof is very straightforward and similar to Theorem 2 and is omitted.

4 \(T_0-\)periodicity and unique periodic attractor

When the resource function K(t, x) and positive distribution P(t, x) are both space and time-dependent, generally, there is no more a positive equilibrium solution of (1)-(3) without having the effect of harvesting. However, if P(t, x), K(t, x) and r(t, x) are periodic bounded functions with the same period \(T_0\), under certain conditions, we can establish the existence of a positive attracting periodic solution.

Recall again the substitution \(w=v/P\), where P is assumed to be strictly positive, bounded, Hölder continuous in x, periodic and at least \(C^1(\mathbb {R}_+)\) in t. Then the problem (1)-(3) with \(Y_h(t,x)\equiv 0\) becomes

$$\begin{aligned} \frac{\partial w}{\partial t}- \frac{d}{P} \Delta w&= rw \left( 1- \frac{Pw}{K} \right) - \beta w, \; (t,x)\in {\Gamma }, \end{aligned}$$
(27)
$$\begin{aligned} \frac{\partial w}{\partial n}&=0,\; (t,x) \in {\partial \Gamma }, \end{aligned}$$
(28)
$$\begin{aligned} w(0,x)&=\frac{v(0,x)}{ P(0,x)},\; x\in {\Omega }, \end{aligned}$$
(29)

where \(\beta (t,x)=\frac{1}{P}\frac{\partial P}{\partial t}\).

We also denote \(g_{\min }= \inf \left\{ g(t,x), (t,x) \in {\overline{\Gamma }} \right\} \) and \( g_{\max }=\sup \left\{ g(t,x),(t,x)\in {\overline{\Gamma }}\right\} ,\) for any bounded continuous function g(t, x).

Theorem 4

Suppose that \(r_{\min }-\beta _{\max }>0\) and

$$\begin{aligned} 2 H \;r_{\min }(r_{\min }-\beta _{\max })-r_{\max } \left( r_{\max }- \frac{\beta _{\min }}{2} \right) >0, \end{aligned}$$
(30)

where H is defined in (7), then there exists a unique periodic solution \(w^*\) of (27)-(29) in the interval

$$\begin{aligned} \left\langle \frac{r_{\min }-\beta _{\max }}{r_{\max }}, \frac{r_{\max }-\beta _{\min }}{r_{\min }} \right\rangle . \end{aligned}$$

Proof

Denote

$$\begin{aligned} \underline{w}= \frac{r_{\min }-\beta _{\max }}{r_{\max }}, \; \overline{w}= \frac{r_{\max }-\beta _{\min }}{r_{\min }}. \end{aligned}$$

It is easy to check that

$$\begin{aligned}&\frac{\partial \underline{w}}{\partial t}-\frac{d}{P} \Delta \underline{w} =0= \underline{w} \left( r_{\min }- \beta _{\max }- r_{\max }H\underline{w} \right) \le \underline{w} \left( r- \beta - r \frac{P}{K} \underline{w} \right) ,\\&\frac{\partial \overline{w}}{\partial t}-\frac{d}{P} \Delta \overline{w} =0= \overline{w} \left( r_{\max }- \beta _{\min }- r_{\min }H\overline{w} \right) \ge \overline{w} \left( r- \beta - r \frac{P}{K} \overline{w} \right) . \end{aligned}$$

These inequalities imply that \(\underline{w}\) and \(\overline{w}\) are the constant lower and upper solutions of (27)-(29) with the initial conditions \(w(0,x)= \underline{w}\) and \(\overline{w}\), respectively. Then according to Lemma A4 from Appendix there exists a pair of \(T_0\)-periodic solutions \(w_*\) and \(w^*\) satisfying

$$\begin{aligned} \underline{w} \le&w_*(t,x) \le w^*(t,x) \le \overline{w}, \; (t,x) \in {\Gamma }, \end{aligned}$$
(31)
$$\begin{aligned} \frac{\partial w_*}{\partial t}- \frac{d}{P} \Delta w_*=&w_* \left( r(t,x)- \beta (t,x) - r H w_* \right) ,\; (t,x) \in {\Gamma }, \end{aligned}$$
(32)
$$\begin{aligned} \frac{\partial w^*}{\partial t}- \frac{d}{P} \Delta w^*=&w^* \left( r(t,x)- \beta (t,x) - r H w^* \right) ,\; (t,x) \in {\Gamma }, \end{aligned}$$
(33)
$$\begin{aligned} \frac{\partial w_*}{\partial n}=&\frac{\partial w^*}{\partial n}=0, \; (t,x) \in {\partial \Gamma }. \end{aligned}$$
(34)

Now we will show that \(w_* \equiv w^*\) if condition (30) holds. Subtracting (32) from (33), we construct

$$\begin{aligned} \frac{\partial }{\partial t}(w^*-w_*) - \frac{d}{P}\Delta (w^*-w_*)=r(w^*-w_*)- \beta (w^*-w_*) - r H (w^{*2}-w_*^2). \end{aligned}$$
(35)

Introducing \(s:=(w^*-w_*)\sqrt{P}\) in the above equation, we have

$$\begin{aligned} \frac{\partial }{\partial t}\left( \frac{s}{\sqrt{P}} \right) - \frac{d}{P}\Delta \left( \frac{s}{\sqrt{P}} \right) =r\left( \frac{s}{\sqrt{P}} \right) - \beta \left( \frac{s}{\sqrt{P}} \right) - r H \left( \frac{s}{\sqrt{P}} \right) (w^{*}+w_*). \end{aligned}$$
(36)

Rearranging

$$\begin{aligned}&\frac{1}{\sqrt{P}} \frac{\partial s}{\partial t}- \frac{1}{2} \frac{s}{P^{3/2}} \frac{\partial P}{\partial t}=\frac{d}{P}\Delta \left( \frac{s}{\sqrt{P}} \right) +r\left( \frac{s}{\sqrt{P}} \right) \nonumber \\&\quad - \beta \left( \frac{s}{\sqrt{P}} \right) - r H \left( \frac{s}{\sqrt{P}} \right) (w^{*}+w_*). \end{aligned}$$
(37)

Multiplying both sides of (37) by \(s\sqrt{P}\) and rearranging, we have

$$\begin{aligned} s \frac{\partial s}{\partial t}=d \frac{s}{\sqrt{P}} \Delta \left( \frac{s}{\sqrt{P}} \right) +s^2\left( r- \frac{\beta }{2}\right) - r H s^2 (w^*+w_*). \end{aligned}$$
(38)

Due to periodicity of \(K,P,w^*\), and \(w_*\), the function s(t, x) is also \(T_0\)-periodic, therefore

$$\begin{aligned} \begin{aligned} 0&= \int \limits _{0}^{T_0} \int \limits _{\Omega } s \frac{\partial s}{\partial t}\;dx\;dt \\&= -d \int \limits _{0}^{T_0} \int \limits _{\Omega } \Big |\nabla \left( \frac{s}{\sqrt{P}} \right) \Big |^2\;dx\;dt +\int \limits _{0}^{T_0} \int \limits _{\Omega } s^2\left[ \left( r- \frac{\beta }{2}\right) - r H (w^*+w_*) \right] \;dx\;dt \\&\le -d \int \limits _{0}^{T_0} \int \limits _{\Omega } \Big |\nabla \left( \frac{s}{\sqrt{P}} \right) \Big |^2\;dx\;dt\\&\quad - \left[ 2 H r_{\min }(r_{\min }- \beta _{\max })- r_{\max } \left( r_{\max } - \frac{\beta _{\min }}{2} \right) \right] \int \limits _{0}^{T_0} \int \limits _{\Omega } s^2 \;dx\;dt \\&\le 0. \end{aligned} \end{aligned}$$

In the first inequality of the previous line we used \(w^*+w_* \ge 2\underline{w}\); the last inequality follows from the condition (30). Therefore \(w^*-w_*=0\) and we obtain a unique periodic solution \(w^*=w_*=\hat{w}\) of (27)-(29) in the interval \(\langle \underline{w}, \overline{w} \rangle \). Moreover, according to Lemma A4 for any initial function \(w_0(x) \in {\langle \underline{w}, \overline{w} \rangle }\) the corresponding solution of (27)-(29) satisfies \(w(t,x)\rightarrow \hat{w}(t,x)\) as \(t\rightarrow \infty \) for \(x \in {\overline{\Omega }}\). \(\square \)

5 Persistence and extinction with harvesting

We now consider the harvesting term effect (i.e., \(Y_h(t,x)\not \equiv 0\)) in the system (1)-(3) to explore some advanced study connected between intrinsic growth rate, carrying capacity, and harvesting function.

Introducing \( w= v/P\) in system (1)-(3) becomes

$$\begin{aligned} \frac{\partial w}{\partial t}- \frac{d}{P} \Delta w&=-\frac{1}{P} \frac{\partial P}{\partial t} w +rw \left( 1- H w\right) -Y_hw , (t,x)\in {\Gamma }, \end{aligned}$$
(39)
$$\begin{aligned} \nabla w \cdot n&=0,\; (t,x) \in {\partial \Gamma }, \end{aligned}$$
(40)
$$\begin{aligned} w(0,x)&=\frac{v(0,x)}{P(0,x)},\; x\in {\Omega }. \end{aligned}$$
(41)

The system (39)-(41) also has a unique positive solution, and we have the following result.

Theorem 5

Let \(v_0(x) \in {C(\Omega )}, \; v_0(x)>0\) in \(\Omega \), then there exists a unique positive solution v(t, x) of the problem (1)-(3).

Proof

The proof of the theorem follows using after the immediate substitution of (1)-(3), which brings out (39)-(41) and as a consequence of the proof of Theorem 1. According to Theorem 1, to prove it, we only need to construct an upper-lower solution pair. Consider a constant C as in (9) then \(r(t,x)(1-H C) <0\) which can be found according to (h2). Furthermore, choose \(\gamma _1 \ge \sup \limits _{(t,x)\in {\Gamma }} \left| \frac{1}{P} \frac{\partial P}{\partial t}-Y_h(t,x) \right| \) and let \(\overline{w}(t,x) \equiv Ce^{\gamma _1 t}\) which is valid since \(v_0\) is bounded in \(\overline{\Gamma }\) and K, and P are bounded from below. Then

$$\begin{aligned} \frac{\partial \overline{w}}{\partial t}- \frac{d}{P} \Delta \overline{w}= \gamma _1 \overline{w}, \text {gives}\nonumber \\ \overline{w} \left( r- r H \overline{w}- \frac{1}{P}\frac{\partial P}{\partial t}+Y_h \right) \le \gamma _1 \overline{w}. \end{aligned}$$
(42)

Further,

$$\begin{aligned} \frac{\partial \overline{w}}{\partial n} =0 \; \text {and} \; \overline{w} \ge w(0,x). \end{aligned}$$

Therefore, \(\overline{w}(t,x)\) is an upper solution of (39)-(41) by Definition A2. The function \(\underline{w}(t,x) \equiv 0\) is obviously a lower solution. The right-hand side function of (39)-(41)

$$\begin{aligned} g(t,x,w,K,P):= rw \left( 1- H w \right) - \left( \frac{1}{P}\frac{\partial P}{\partial t}+ Y_h\right) w \end{aligned}$$

is continuously differentiable with respect to w and we can denote the maximal derivative of g in w for each (t, x) such that

$$\begin{aligned} \underline{g}(t,x)&= \sup \left\{ -g_w(t,x,w,K,P),\,\underline{w} \le w \le \overline{w} \right\} ,\text {and}\\ \overline{g}(t,x)&= \sup \left\{ g_w(t,x,w,K,P),\,\underline{w} \le w \le \overline{w} \right\} . \end{aligned}$$

Then, the Lipschitz condition (59) holds and by Lemma A2 there exists a unique solution of the problem (1)-(3) satisfying \(\underline{w} \le w \le \overline{w}\). The positivity of the solution is obvious according to Theorem 1. \(\square \)

In the following stairs, we will consider the case where all the functions are time-independent, and we assume \(K(t,x)\equiv K(x)\), \(P(t,x)\equiv P(x)\), \(r(t,x)\equiv r(x)\), and \(Y_h(t,x)\equiv Y_h(x)\). Thus, the system (1)-(3) becomes

$$\begin{aligned} \frac{\partial v}{\partial t} =&\, d\Delta \left( \frac{v}{P(x)} \right) + r(x)v\left( 1-\frac{v}{K(x)} \right) -Y_h(x)v, \; (t,x) \in \Gamma , \end{aligned}$$
(43)
$$\begin{aligned} \nabla \left( \frac{v}{P(x)} \right) \cdot n=&\, 0, \; (t,x) \in {\partial \Gamma }, \end{aligned}$$
(44)
$$\begin{aligned} v(0,x)=&\, v_0(x), \;x\in {\Omega }. \end{aligned}$$
(45)

To study the problem (43)-(45), we first consider the following two propositions for a general parabolic equation as described in [17].

Proposition 1

( [17], Proposition 3.1) Consider the following general form of a model

$$\begin{aligned} \frac{\partial v}{\partial t}=&\, \nabla \cdot d(x)\nabla v + \vec {b}(x) \cdot \nabla v + f(x,v) \; in \; \Omega \times (0, \infty ), \end{aligned}$$
(46)
$$\begin{aligned} d(x)\frac{\partial v}{\partial n}+ \beta _1(x) v =&\, 0 \; on \; \partial \Omega \times (0, \infty ). \end{aligned}$$
(47)

Assume that \(f(x,v) \le v g_0(x)\) for \(x\in {\Omega }\), where \(g_0(x)\) is a bounded measurable function if \(\vec {b}/d\) is a gradient, and \(g_0(x)\in {C^{\alpha }(\overline{\Omega })}\) if \(\vec {b}/d\) is not a gradient. If the largest eigenvalue \(\sigma _1\) of

$$\begin{aligned}&\nabla \cdot d(x)\nabla \psi + \vec {b}(x) \cdot \nabla \psi +g_0(x) \psi =\, \sigma \psi \; in \; \Omega \times (0, \infty ), \end{aligned}$$
(48)
$$\begin{aligned}&d(x)\frac{\displaystyle \partial \psi }{\displaystyle \partial n}+ \beta _1(x) \psi = 0 \; on \; \partial \Omega \times (0, \infty ), \end{aligned}$$
(49)

is negative, then (46)-(47) has no positive equilibria, and all non-negative solutions decay exponentially to zero as \(t \rightarrow \infty \).

Proposition 2

([17], Proposition 3.2, and 3.3) Suppose that \(f(x,v)=v g(x,v)\) with g(x, v) of class \(C^2\) in v and \(C^{\alpha }\) in x and there exists a \(L>0\) such that \(g(x,v)<0\) for \(v>L\). If the principal eigenvalue \(\sigma _1\) is positive in the problem

$$\begin{aligned}&\nabla \cdot d(x)\nabla \psi + \vec {b}(x) \cdot \nabla \psi +g(x,0) \psi = \sigma \psi \; in \; \Omega \times (0, \infty ),\\&d(x)\frac{\displaystyle \partial \psi }{\displaystyle \partial n}+ \beta _1(x) \psi = 0 \; on \; \partial \Omega \times (0, \infty ), \end{aligned}$$

then (46)-(47) has a minimal positive equilibrium \(v^*\), and all solutions to (46)-(47) which are initially positive on an open subset of \(\Omega \) are eventually bounded below by orbits which increase toward \(v^*\) as \(t \rightarrow \infty \). Moreover, if g(x, v) is strictly decreasing in v for \(v \ge 0\) then the minimal positive equilibrium is the only positive equilibrium for (46)-(47).

Now we will demonstrate sufficient conditions for extinction and persistence for the harvesting model (43)-(45).

Theorem 6

Let the function \(f(t,x,v,K):= r(x) v(1- v/K)\) satisfies the assumptions (h1)-(h2) and let \(\sup \limits _{t>0} [r(x) (1- v/K)] < Y_h(x)\) for all \(x\in {\Omega }\). Then for any \(v_0(x)\) the solution of system (43)-(45) converges to zero as \(t \rightarrow \infty \).

Proof

Once again, we assume \(w(t,x)=\frac{v}{P(x)}\) and then Eq. (43)-(45) becomes

$$\begin{aligned} \frac{\partial w}{\partial t} =&\frac{d}{P(x)}\Delta w + r(x)w\left( 1-\frac{ P(x) w}{K(x)} \right) -Y_h(x)w, \; (t,x) \in \Gamma , \end{aligned}$$
(50)
$$\begin{aligned} \nabla w\cdot n=&0, \; (t,x) \in {\partial \Gamma }, \end{aligned}$$
(51)
$$\begin{aligned} w(0,x)=&\frac{v_0(x)}{P(x)}, \;x\in {\Omega }. \end{aligned}$$
(52)

Rewrite the term \(\frac{ d}{ P(x)}\Delta w\) as:

$$\begin{aligned} \frac{\displaystyle d}{ \displaystyle P(x)}\Delta w = \nabla \cdot \left( \frac{d}{P(x)} \nabla w\right) - \nabla \frac{d}{P(x)} \cdot \nabla w. \end{aligned}$$

Therefore, comparing (50)-(52) with (46)-(47), it shows that \(d(x)=\frac{d}{P(x)}\), \(\vec {b}(x)= - \nabla \frac{d}{P(x)}\), \(f(x,v)=rw(1-Pw/K)-Y_hw\), and \(\beta _1(x)=0\).

Denote

$$\begin{aligned} \sup \limits _{t>0} \left[ r(x)\left( 1-\frac{P(x) w}{K(x)} \right) -Y_h(x)\right] =g_0(x) \; \text {for} \; x\in {\Omega }. \end{aligned}$$

Then the linearized eigenvalue problem of (50)-(52) around the solution w(t, x) is given by

$$\begin{aligned} \frac{\displaystyle d}{ \displaystyle P(x)}\Delta \psi + g_0(x)\psi =&\sigma \psi , \, (t,x) \in \Gamma , \end{aligned}$$
(53)
$$\begin{aligned} \nabla \psi \cdot n=&0, \, (t,x) \in {\partial \Gamma }. \end{aligned}$$
(54)

To prove the result, it is enough to show that the principal eigenvalue of (53)-(54) is negative. Multiplying both sides of (53) by P(x), and integrating over \(\Omega \) using the boundary condition, sequentially, we get

$$\begin{aligned} \sigma \int \limits _{\Omega } P(x)\psi \; dx =\int \limits _{\Omega } P(x)g_0(x)\psi \; dx. \end{aligned}$$

Therefore, the principal eigenvalue is

$$\begin{aligned} \sigma _1 = \sup \limits _{(t,x)\in {\Gamma }} \frac{\int \limits _{\Omega } P(x)g_0(x)\psi \; dx}{\int \limits _{\Omega } P(x)\psi \; dx}. \end{aligned}$$

From the initial assumption, we have \(\sup \limits _{t>0} [r(x) (1- v/K)] < Y_h(x)\) such that

$$\begin{aligned} g_0(x)=\sup \limits _{t>0} \left[ r(x)\left( 1-P w/K \right) -Y_h(x) \right] <0. \end{aligned}$$

Hence, \(\sigma _1 <0\), which concludes the proof. \(\square \)

Theorem 7

Let the function \(f(t,x,v,K):= r(x) v(1- v/K)\) hold the conditions (h1)-(h3) and let \(\sup \limits _{t>0} [r(x) (1- v/K)] > Y_h(x)\) for \(x\in {\Omega }\). This guarantees a unique positive equilibrium state \(v^*(x)\) of (43)-(45) such that \(v_0 \in {C(\Omega )}\), \(v_0 \not \equiv 0\), as t approaches to the infinity, v(t, x) converges to the \(v^*(x)\).

Proof

If we compare the system (50)-(52) which is equivalent to (43)-(45), with system (46)-(47), then we get the linearized system around the solution w(t, x) given by

$$\begin{aligned} \frac{\displaystyle d}{ \displaystyle P(x)}\Delta \psi + g(x,w)\psi =\sigma \psi , \; (t,x) \in \Lambda ,\nabla \psi \cdot n=0, \; (t,x) \in {\partial \Lambda }. \end{aligned}$$

where,

$$\begin{aligned} g(x, w)=\sup \limits _{t>0} \left[ r(x)\left( 1-\frac{\displaystyle P(x) w(t,x)}{\displaystyle K(x)} \right) -Y_h(x)\right] \; \text {for} \; x\in {\Omega } \end{aligned}$$

By integrating and using the boundary condition we get

$$\begin{aligned} \sigma \int \limits _{\Omega } P(x)\psi \; dx =\int \limits _{\Omega } P(x)g(x,w)\psi \; dx \end{aligned}$$

Which gives us the principal eigenvalue

$$\begin{aligned} \sigma _1 = \sup \limits _{(t,x)\in {\Lambda }} \frac{\int \limits _{\Omega } P(x)g(x, w)\psi \; dx}{\int \limits _{\Omega } P(x)\psi \; dx}, \end{aligned}$$

Since g(x, w) is strictly positive from the initial assumption that \(\sup \limits _{t>0} [r(x) (1- v/K)] > Y_h(x)\) for all \(x\in {\Omega }\), we can conclude that \(\sigma _1 >0\).

Also,using the properties (h2) there exists K such that

$$\begin{aligned} g(x,w):= r(x) (1- Pw/K) - Y_h(x) < 0, \;\text {while}\; w>K/P, \end{aligned}$$

Hence the function g(x, w) is decreasing in w for \(w \ge K/P>0\). By comparing with Proposition 2, there exists a unique positive equilibrium solution \(w^*\) of (50)-(52) as equivalence to \(v^*\) of (43)-(45).

To show that, the equilibrium solution \(v^*\) is bounded, we can use upper-lower solution pair according to Lemma A2 as defined in Appendix A. The proof is very similar to Theorem 5. For simplicity we will use model (50)-(52). To construct an upper solution, consider a constant c such that

$$\begin{aligned} c \ge \sup \limits _{x\in {\Omega }} \left[ \frac{K(x)}{P(x)}\right] , \end{aligned}$$

then \(r(x)\left( 1-\frac{P}{K} C\right) <0\). Further, choose \(\gamma _2 \ge \sup \limits _{x\in {\Omega }} \left| Y_h(x) \right| \) and let \(\overline{w}(t,x) \equiv ce^{\gamma _2 t}\) which is valid since \(v_0\) is bounded in \(\overline{\Lambda }\) and K and P are bounded below in \(\Omega \). Then

$$\begin{aligned} \frac{\partial \overline{w}}{\partial t}- \frac{d}{P} \Delta \overline{w}= \gamma _2 \overline{w} \ge \overline{w} \left( r- \frac{rP}{K} \overline{w}- Y_h \right) , \end{aligned}$$

Also,

$$\begin{aligned} \frac{\partial \overline{w}}{\partial n} =0 \; \text {and} \; \overline{w} \ge w(0,x). \end{aligned}$$

Therefore \(\overline{w}(t,x)\) is an upper solution of (50)-(52) by Definition A2. The function \(\underline{w}(t,x) \equiv 0\) is obviously a lower solution. Since the steady-state is unique and bounded by upper and lower solution, so it is asymptotically stable, i.e., \(v(t,x)\rightarrow v^*(x)\) as \(t \rightarrow \infty \) for any \(v_0 \ne 0\). \(\square \)

6 Numerical simulations

In this section we perform several numerical experiments with and without harvesting effect in the model. For numerical computation, we discretize the Eqs. (1)-(3) using Crank-Nicolson scheme, which is unconditionally stable.

6.1 Numerical illustrations without harvesting

Example 1

Assume that \(P(t,x)=(2.3+\cos (\pi x))(1.2+\sin (t))\) on \(\Omega =(0,1)\) with the diffusion coefficient \(d=1.0\), and the reaction coefficient \(r(x)=1.1\). If \(K(t,x)/P(t,x)\equiv k\) where k is a constant, for example, \(K(t,x)=\alpha P(t,x)\), and \(\alpha =2.0\) then there is a unique solution of (1)-(3).

Fig. 1
figure 1

Average solutions of (1)-(3) using different initial values for (a) \(r(x)=1.1\), (b) \(r(x)=2.1+\cos (\pi x)\), and (c) \(r(t,x)=(2.1+\cos (\pi x))(1.5+\cos (t))\), where \(P(t,x)=(2.3+\cos (\pi x))(1.2+\sin (t))\), \( K(t,x)=2P(t,x)\), \(\Omega =(0,1)\), and \(d=1.0\)

Full size image

If we compare the uniqueness for various initial conditions and different growth rates, the unique solution of (1)-(3) is valid as designed in Fig. 1. This figure justified the result of Theorem 1 for proportional functions P(t, x) and K(t, x).

In the following example, we consider the arbitrary time-dependent function to check the positivity and uniqueness of solution for the system (1)-(3) by changing the initial densities.

Example 2

Suppose \(P(t,x)=(2.3+\cos (\pi x))(1.2+\sin (t))\) on \(\Omega =(0,1)\) with the diffusion coefficient \(d=1.0\), and reaction coefficient \(r(x)=1.1\). If \(K(t,x)=(2.5+\cos (\pi x))(1.3+\sin (t))\), there is a unique solution of (1)-(3) as shown in Fig. 2, where we choose various positive initial values \(v_0\in \left\{ 0.7, 1.5, 7.2 \right\} \) to justify the uniqueness of solutions.

Fig. 2
figure 2

Solutions of (1)-(3) a over the domain, and b over time, for \(r(x)=1.1\), \(P(t,x)=(2.3+\cos (\pi x))(1.2+\sin (t))\), \(K(t,x)=(2.5+\cos (\pi x))(1.3+\sin (t))\), \(\Omega =(0,1)\), \(d=1.0\), and for the varying initial conditions

Full size image

Graphical structure of these diagrams (Fig. 2) verified the Theorem 1 for random, non-proportional and time-periodic functions P(t, x), and K(t, x).

In both Examples 1 and 2 (Figs. 1 and 2), Theorem 1 is verified either for proportional or non-proportional relations of the distribution function P(t, x) and the carrying capacity K(t, x), i.e., the bounded H defined in (7) does not affect the main result of the Theorem 1.

For Example 3, we consider the spatially distributed rational function to show the effects of different parameters.

Example 3

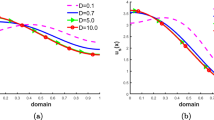
In this example, we consider \(P(x)=2.0+\cos (\pi x)\) on \(\Omega =(0,1)\) with the diffusion coefficient \(d=1.0\), and reaction coefficient \(r(x)=2.1+\cos (\pi x)\). If \(K(x)=\alpha P(x)\), and \(\alpha =2.5\) there is a unique solution of (14)-(16) as designed in Fig. 3 due to the outcome of diffusion coefficients and multiple initial values.

Fig. 3
figure 3

Average solutions of (14)-(16) over time for \(P(x)=2.0+\cos (\pi x)\), \(K(x)=2.5P(x)\), \(r(x)=2.1+\cos (\pi x)\), and \(\Omega =(0,1)\) in a convergence study for \(v_0=0.55\), and \(d=1.0\), b effects of diffusion coefficients where \(v_0=0.55\), and c for different initial values with \(d=1.0\)

Full size image

Figure 3 ensures the result as justified in Theorem 3 for spatially distributed rational functions P(x) and K(x).

Since there exists a unique solution that converges to K(x), which is also true if we vary diffusion coefficient, d and initial density, \(v_0\) (Fig. 3). Also, the conclusion of the Theorem 3 is stable for varying reaction coefficients, as depicted in Fig. 4.

Fig. 4
figure 4

Solutions of (14)-(16) (a) over the domain, and (b) average solutions with respect to time for \(P(x)=2.0+\cos (\pi x)\), \(K(x)=2.5P(x), \; \Omega =(0,1)\), \(v_0=0.5\), and \(d=1.0\) with the variation of reaction coefficients \(r=1.0,\;2.1\), and \(r(x)=2.1+\cos (\pi x)\).

Full size image

Finally, from those Figs. (3 and 4), we see that for proportionally changes distribution function if we alter diffusion coefficient d, initial density \(v_0\), and reaction coefficient r(x), the behavior of solution does not show any significant change and always converges to K(x) at \(t\rightarrow \infty \).

At this stage, our interest is to consider the arbitrary function to observe and check the validity of theoretical results by changing the parametric values.

Example 4

In this problem, we consider \(P(x)=2.0+\cos (\pi x)\) on \(\Omega =(0,1)\) with the diffusion coefficient \(d=1.0\), reaction coefficient \(r(x)=2.1+\cos (\pi x)\), and \(v_0=0.5\). We assume the carrying capacity \(K(x)=\alpha P(x)+c, \text {where}\; \alpha =2.5>0\), and \(c=3.0>0\). There is a unique solution of (14)-(16), which justifies Theorem 2 for the non-rational functions P(x) and K(x) (Fig. 5).

Fig. 5
figure 5

Solutions of (14)-(16) a over the domain and b average solutions with time for \(P(x)=2.0+\cos (\pi x)\), \(K(x)=2.5P(x)+3.0\), \(\Omega =(0,1)\), \(d=1.0\), and \(v_0=0.5\)

Full size image

Since it is not necessary here that the solution converges to K(x), it might converge to K(x) or not depending on the environment, which is also true if we vary the diffusion coefficient (Fig. 6(a)); specific growth rate (Fig. 6(b)) and the initial density (Fig. 6(c)).

Fig. 6
figure 6

Average solutions of (14)-(16) over time for \(P(x)=2.0+\cos (\pi x)\), \(K(x)=2.5P(x)+3.0\), \(r(x)=2.1+\cos (\pi x)\), and \(\Omega =(0,1)\) in a effects of diffusion coefficients where \(v_0=0.5\), b for different growth rates when \(d=1.0\), and c for different initial values with \(d=1.0\)

Full size image

Observing all figures (Fig. 6), it concludes that for arbitrary distribution function, if we vary the initial density of \(v_0\), then the solution doesn’t diverge. If we choose a different diffusion coefficient d, then a slight change will be noticed. Lastly, if we dealt with the variation of reaction coefficient r(x), the behavior of the solution changes rapidly, showing the speed of convergence.

6.2 Numerical illustrations with harvesting

Example 5

In model (43)-(45), we consider the spatial functions \(P(x)=1.3+\cos (\pi x)\), \(K(x)=2.1+\cos (\pi x)\), the diffusion coefficient \(d=1.0\), and initial values \(v_0=0.1\). The result in Fig. 7 follows the analytical behavior. We consider in (a) \(r=1.2\) with various constant and non-constant harvesting functions, \(Y_h=1.0,\; 1.3,\; Y_1(x)= 0.1+(\cos (\pi x))^2, \; Y_2(x)=1.4+\sin (\pi x)\), and in (b) \(r=1.5+\cos (\pi x)\sin (x)\) with \(Y_h=1.0,\; 1.55,\; Y_3(x)=0.1+(\sin (x))^2\), and \(Y_4(x)=1.6+\sin (\pi x)\).

Fig. 7
figure 7

Average solutions of (43)-(45) over time for \( P(x)=1.3+\cos (\pi x)\), \( K(x)=2.1+\cos (\pi x), \; \Omega =(0,1)\), and \( d=1.0\) with \(v_0=0.1\)

Full size image

When we allow harvesting, as in (43)-(45), numerical study shows that if the growth rate per capita is lower than the harvesting, either spatially distributed or constant, the density of average population levels eventually dropped to zero as time grows. On the other scenarios, if the harvesting coefficient is lower than the specific growth rate, the population has a stable state and this fact is analytically proved in Theorems 6 and 7.

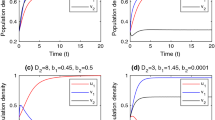
Example 6

Similarly, in (1)-(3), we consider the time-varying rational function, \(K(t,x)\equiv 2 P(t,x)\); where \(P(t,x)= (2.3+\cos (\pi x))(1.2+ \sin (t))\), growth rate \(r=1.0\), diffusion coefficient \(d=1.0\), and initial density \(v_0=0.1\). In Fig. 8, we consider harvesting coefficient in (a) \(Y_h=1.1\); in (b) \(Y_h=0.5\); and in (c) \(Y_h(x)=0.5+(\cos (\pi x))^2\). This example also shows that the population is in extinction if the harvesting rate is high, see Figure 8(a), whereas the population persists periodically for higher growth rate, see for examples in Fig. 8b and 8c.

Fig. 8
figure 8

Average solutions of (1)-(3) over time for \( P(t,x)=(2.3+\cos (\pi x))(1.2+ \sin (t))\), and \( K(t,x)=2P(t,x)\) on the domain \(\Omega =(0,1)\), \(r=1.0\), and \( d=1.0\) with \(v_0=0.1\) for a \(Y_h=1.1\); b \(Y_h=0.5\); c \(Y_h(x)=0.5+(\cos (\pi x))^2\)

Full size image

Example 7

In (1)-(3), we now assume the time-periodic non-rational parameters such that \(P(t,x)=(1.3+\cos (\pi x))(1.2+\sin (t))\), \(K(t,x)=(2.1+\cos (\pi x)) (1.05+\sin (t))\), \(r(t,x)=1.8+\cos (\pi x)\sin (t)\), with constant diffusion rate \(d=1.0\), and initial density \(v_0=0.1\). It is seen that the graphs follow the theoretical results, see Fig. 9 for (a) \(Y_h(t,x)=2.1+ \sin (x)\cos (t)\), (b) \(Y_h(t,x)=1.1+ \sin (x)\cos (t)\), and (c) \(Y_h(t,x)=1.1+\cos (t)\). By choosing all functions in both space-time periodic, we conclude that there exists a positive solution that has been proven theoretically in Theorem 5.

Fig. 9
figure 9

Periodic solution of (1)-(3) with time for \( P(t,x)=(1.3+\cos (\pi x))(1.2+\sin (t))\), \( K(t,x)=(2.1+\cos (\pi x)) (1.05+\sin (t))\), \(r(t,x)=1.8+\cos (\pi x)\sin (t)\), \(\Omega =(0,1)\), \(d=1.0\), and initial value \(v_0=0.1\) with a \(Y_h(t,x)=2.1+ \sin (x)\cos (t)\), b \(Y_h(t,x)=1.1+ \sin (x)\cos (t)\), and c \(Y_h(t,x)=1.1+\cos (t)\)

Full size image

7 Conclusion

In this paper, we studied a reaction-diffusion model for single species with logistic growth function, where carrying capacity, K and distribution function, P are time dependent. We showed that for the described model, there exists unique solution (whether the distribution function P(t, x) is proportional to carrying capacity K(t, x) or not) and it is positive by using upper and lower solution method. The model is also valid for time independent carrying capacity. If the distribution function P(x) is proportional to K(x) then there exists unique solution v(t, x) which converges to K(x) with the convergence speed \( \int \limits _{\Omega } |v(t,x)-K(x)|dx \le e^{-\Upsilon t} \int \limits _{\Omega } K(x)\;dx \). On the other hand if K(x) and P(x) are non-proportional then it is not guaranteed that the solution will converge to K(x). If the carrying capacity, K(t, x) and distribution function, P(t, x) is a time-periodic function, then we showed that there has a unique periodic solution in some intervals with a threshhold dynamics. At the inclusion of the harvesting term, we studied the modified model and established several results connected with the time-spatial specific growth rate and harvesting function. The results reflect the natural phenomena of various species, as introduced in the earlier section of this study. Some numerical results were illustrated to justify the analytic results in a non-empty open domain for various parametric values with different initial conditions.

In the COVID era, with the initiative of One Health Research Coalition [43], the importance of the transdiciplinary research across environmental sciences and public health is highly encouraged. Recent reports show that COVID-19 can be spread to animals from human, and vice-versa [44]. In the future work, we plan to incorporate the COVID-19 models to our model following the recent works [45,46,47,48,49] to have the pandemic impact on the ecological results. To model and analyze the density of the species using fractional order derivative following the recent investigations in [50,51,52,53] and along with the idea herein could be a next research avenue.