1 Introduction

The coronavirus pandemic and their new strains are major threat for mankind. The world globalization has accelerated the rapid spread of infections in a short period of time. This affects the public health care system and also hinders the economic development of the developing and underdeveloped countries. Since the start of the epidemic outbreaks, it is estimated that the global disease burden due to COVID-19 amounts to over 92 million reported cases and 2 million deaths worldwide [1]. COVID-19 virus constantly changes through mutation and a new variant has begun circulating in UK, as a result, a novel complete lockdown has been imposed to cope up with the new epidemic wave. COVID-19 is wreaking havoc on the whole world at present, after its emergence in Wuhan in December 2019 and the subsequent global spread since February 2020. The disease, being caused by novel coronavirus (nCoV-SARS), is a new member of the coronavirus family. Although researchers are actively involved in studying and trying to understand the virus features and its epidemiology, the accurate knowledge about the disease is still very limited. This calls for scientific studies to explore and understand the mechanism behind the spread of virus and to examine the impacts of various pharmaceutical and non-pharmaceutical measures on its control [2]. The spread of COVID-19 across 223 countries is causing a serious threat to the world population [3]. During the lockdowns people in different countries have patiently been waiting for the development of an effective treatment strategy and the development of a vaccine. But it is imperative to be able to forecast the COVID-19 cases for designing effective strategies and policy making to fight the pandemic, and heal the scars that it is leaving behind on the lives of the people and on the global economy [4].

At the time of a pandemic, during the early stages of the spread of the infection, when health care demands and other biomedical interventions are not sufficient to protect the people against the new emerging disease, the best way to reduce the disease transmission is to adequately inform the people about non-pharmaceutical interventions and extreme precautionary measures. This can be peformed through social media in an easy, fast and inexpensive way and can help in suppressing the disease spread: e.g. by using radio (which is cost effective and responsive medium in remote areas), TV, internet [5,6,7]. In contemporary times, media coverage is identified as an alternate control measure which brings behavioral changes among susceptible individuals, can be seen as partial treatment at no cost [8,9,10]. People become alert due to media campaigns and take necessary precautions to avoid their contacts with infected individuals [11,12,13]. The individuals who are substantially aware of transmission mechanisms, adjust their routine work, travel and pay significant attention on isolating themselves and use precautionary measures, and hence reduce their possibility of contracting the infection. Thus in India and other countries, the severity of COVID-19 diffusion can be reduced by the regular use of media to inform people on the preventive measures to be taken.

A plethora of modeling studies confirmed that awareness programs have the capability to reduce the epidemic threshold and thus control the spread of infection [14,15,16,17,18,19]. Mathematical models have been used to predict the disease dynamics and also to assess the efficiency of the intervention strategies in reducing the disease burden [20, 21]. A number of modeling studies have already been performed for the COVID-19 pandemic [22,23,24,25,26]. Imai et al. [27] conducted computational modeling of potential epidemic trajectories to estimate the size of the disease outbreak in Wuhan, with a focus on the human-to-human transmission. Their results imply that control measures need to block well over 60% of transmission to be effective in containing the outbreak. Several studies have been done using real incidence COVID-19 data of India and examined different characteristics of the outbreak as well as evaluated the effect of intervention strategies implemented to curb the outbreak in India [28,29,30,31,32]. In India, the first confirmed case of COVID-19 was reported on 30th January, 2020 [1]. Government of India declared a countrywide lock-down as a preventive measure for the COVID-19 outbreak on 24th March, 2020 [33]. The government is also continuously using various media and social networking web sites to aware the citizen regarding the current scenario of disease threats and their control mechanisms. They are employing different modes of propagating informations including social media, TV, radio, internet using various types of slogan such as “Stay home, Stay safe”, “Be clean, Be healthy”, “Jab Tak Dawai Nahi, Tab Tak Dhilai Nahi” (No carelessness till a medicine is found), “Do Gaj ki Doori, Mask Hai Jaroori” (Mask and maintaining distance of two yards is necessary), etc. The main motive of such social media campaigns is to stimulate people to adopt healthy sanitation practices, frequent hand washing, use of face mask, sanitizer, maintain social distancing, avoiding touching eyes/nose/mouth etc., [34,35,36]. The findings of [37,38,39,40] suggest that the early implementation of social lockdown and awareness among the individuals regarding social distancing (to avoid inter-individual physical contacts) has drastic impacts on the prevalence of COVID-19, and it also efficiently reduces the environmental pollutants in India. Chang et al. [41] have assessed the impact of media coverage on the spread of COVID-19 in Hubei Province, China. Continuous propagation of information through media campaigns is found to encourage the people to adopt preventive measures to combat the pandemic together. Findings of Zhou et al. [42] suggested that besides improving the medical levels, media coverage can be considered as an effective way to mitigate the disease spreading during the initial stage of an outbreak.

However, the factors like very high population density, the unavailability of specific medicines or vaccines, insufficient evidences regarding the transmission mechanism of the disease also make it difficult to fight against the disease in India. Srivastav et al. [43] have investigated the impacts of face mask, hospitalization of symptomatic individuals and quarantine of asymptomatic individuals on the prevalence of coronavirus pandemic in India. Their findings suggest that the frequent use of face mask while in public places together with hospitalization of symptomatic individuals and quarantine of asymptomatic individuals have potential to suppress the burden of COVID-19 in India. Motivated by the works of Misra et al. [5] and Srivastav et al. [43], and keeping in mind the importance of broadcasting through social media advertisements to encourage people to adopt non-pharmaceutical interventions, the present study aims to assess the impacts of social media advertisements to flatten the disease progress curve on the transmission dynamics of COVID-19 pandemic in India. Our model is different from the model proposed by Srivastava et al. [43] in the following sense. In [43], it is assumed that the constantly and correctly use of face mask reduce the diseases transmission whereas in the present study it is assumed that the broadcasting of global information campaigns through social media advertisements changes the individuals behavioral response towards disease and they adopt practices that are requisite for disease prevention along with use of face mask while in public such as having social distancing, proper sanitation, frequent hand washing, that reduce the contacts between susceptible and symptomatic/asymptomatic individuals. Further, in [43], it is assumed that the recovered individuals do not acquire infection again while medical reports suggest that the recovered individuals may also get infection via losing their immunity as time flows and become susceptible for the disease [44]. Thus, considering reinfection make the model more realistic. Further, in present study, it assumed that the presence of global information campaigns encourage the asymptomatic individuals for conducting health protocols, such as self-isolation, social distancing, etc. We study the effectiveness of social media advertisements in reducing the contact rates of susceptibles with symptomatic/asymptomatic individuals, hospitalization of symptomatic individuals and quarantine of asymptomatic individuals due to influence of social media advertisements on flattening the disease progress curve. Our aim is to investigate how much these intervention strategies can control the spread of coronavirus and whether these control strategies can reduce the burden of COVID-19 in India.

Remainder of the paper is organized in the following way: Sect. 2 contains model formulation and underlying assumptions. In the following section, we obtain disease-free and endemic equilibria of the system. Sufficient conditions are derived for the global asymptotic stability of the endemic equilibrium. We simulate our model in Sect. 4. The model is calibrated using cumulative confirmed COVID-19 cases of India. Sensitivity analysis is performed to identify parameters having crucial impacts on controlling the disease. Finally, the results are compiled and discussed in the closing section.

2 Mathematical model

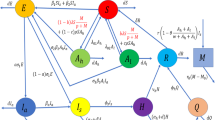
Here, we formulate a compartmental model for dynamics of COVID-19 pandemic in India by considering human-to-human transmission of the disease [45]. We divide the total human population N, into eight compartments: susceptible individuals S, exposed individuals E, symptomatic individuals \(I_s\), asymptomatic individuals \(I_a\), home quarantined asymptomatic individuals Q, aware individuals A, hospitalized individuals H and recovered individuals R. Thus, we have

$$\begin{aligned} N=S+E+I_{s}+I_{a}+Q+A+H+R. \end{aligned}$$

It should be emphasized that the compartment \(I_a\) also contains individuals showing mild symptoms of the disease but are not recognized as COVID-19 infected. Furthermore, the compartment H for hospitalization also includes those with clinical symptoms of COVID-19 who are self-isolating at home. Represent by M, the cumulative number of social media advertisements which includes internet information as well as TV, radio and print media. Suppose \(M_0\) stands for the baseline number of social media advertisements i.e., this number of advertisements are always maintained in the region under investigation. Notably the aware individuals do not mean only the human populations having knowledge of COVID-19 but also those persons who possess the knowledge of avoiding disease transmission and further implementing the prevention mechanisms.

Fig. 1
figure 1

Schematic diagram for system (1). Here, the color of the terms indicates their function. In particular, the red color denotes the impact of awareness programs on the reduction in contact rates of susceptible individuals with symptomatic/asymptomatic individuals, blue color stands for the effect of broadcasting information on awareness of susceptible individuals and green color represents the impact of awareness on the quarantine of asymptomatic individuals

Full size image

For developing the mathematical model, we make the following assumptions.

  1. 1.

    The population is homogeneously mixed and the individuals are recruited in the region at a constant rate \(\varLambda \) and join the susceptible class.

  2. 2.

    In the absence of broadcasting through social media advertisements, the susceptible individuals join the exposed class on effective contacts with symptomatic and asymptomatic infectious human population at the rates \(\beta _1\) and \(\beta _2\), respectively, following simple law of mass action.

  3. 3.

    In the presence of broadcasting through social media advertisements regarding possible control mechanisms and its protective measures, the individuals change their behaviors and adopt practices that are requisite for disease prevention such as wearing face mask, having social distancing, proper sanitation, frequent hand washing, that reduce the contacts between susceptible and symptomatic/asymptomatic individuals [18].

  4. 4.

    A fraction of exposed individuals show clinical symptoms and join the symptomatic class while the remaining join the asymptomatic class. Some of the asymptomatic individuals show clinical symptoms with passage of time and join the symptomatic class at the rate \(\beta _a\) [43].

  5. 5.

    During an endemic outbreak, information is propagated through media and health authorities to warn people through different modes of social media like Facebook, Twitter, WhatsApp.

  6. 6.

    Information broadcasted in public do not remain constant but depend on prevalence of infection, i.e., the growth rate of information campaigns increases in proportion to the number of infected individuals [15].

  7. 7.

    Following [5], we assume that the growth rate of social media advertisements is a decreasing function of aware population in the region. The reason behind such consideration is the involvement of cost in broadcasting the information.

  8. 8.

    As time passes, information broadcasted in public lose their impact. Thus, depletion in cumulative number of advertisements is also incorporated in the model. Moreover, a baseline number of social media advertisements is always maintained in the region.

  9. 9.

    The information broadcasted in public changes individuals’ behaviors towards the disease and the susceptible individuals avoid their contacts with symptomatic and asymptomatic individuals by forming a separate aware class, the individuals in aware class possess the knowledge of avoiding disease transmission and further implementing the prevention mechanism [15]. However, individuals in aware class may lose awareness with the passage of time and become susceptible again at a constant rate \(\lambda _0\).

  10. 10.

    The symptomatic individuals are hospitalized at the rate \(\phi _s\) while in the presence of broadcasting through social media advertisements, the individuals in asymptomatic class move to the quarantined compartment at the rate \(\gamma _a\).

  11. 11.

    The hospitalized and quarantine individuals recovered from COVID-19 through proper treatment or naturally by his/her bodily immune power at a rate \(\phi _h\) and \(\nu _h\), respectively and join the recovered class.

  12. 12.

    The individuals in recovered class lose their immunity as time flows and become susceptible again at a rate \(\delta \).

  13. 13.

    The symptomatic and hospitalized individuals can proceed to severe complications of COVID-19 and experience COVID-19 mortality at a rate \(\alpha _s\) and \(\alpha _h\), respectively. Humans in each class undergo natural mortality at a constant rate d.

These assumptions can be represented by a schematic diagram as depicted in Fig. 1, and the proposed model is given by

$$\begin{aligned} \frac{dS}{dt}= & {} \varLambda -\beta _1\left( 1-c_{m_s}\frac{M}{p+M}\right) SI_s-\beta _2\left( 1-c_{m_a}\frac{M}{p+M}\right) SI_a\nonumber \\&-\lambda SM+\lambda _0A+\delta R-dS,\nonumber \\ \frac{dE}{dt}= & {} \beta _1\left( 1-c_{m_s}\frac{M}{p+M}\right) SI_s+\beta _2\left( 1-c_{m_a}\frac{M}{p+M}\right) SI_a-(\sigma +d)E,\nonumber \\ \frac{dI_s}{dt}= & {} (1-a)\sigma E+\beta _aI_a-(\alpha _s+d)I_s-\phi _sI_s,\nonumber \\ \frac{dI_a}{dt}= & {} a\sigma E-\beta _aI_a-\gamma _aI_aM-dI_a,\\ \frac{dQ}{dt}= & {} \gamma _aI_aM-\phi _hQ-dQ,\nonumber \\ \frac{dA}{dt}= & {} \lambda SM-(\lambda _0+d)A,\nonumber \\ \frac{dH}{dt}= & {} \phi _sI_s-(\nu _h+\alpha _h+d)H,\nonumber \\ \frac{dR}{dt}= & {} \phi _hQ+\nu _hH-(\delta +d)R,\nonumber \\ \frac{dM}{dt}= & {} r\left( 1-\theta \frac{A}{w+A}\right) I_s-r_0(M-M_0).\nonumber \end{aligned}$$
(1)

The initial conditions are considered as,

$$\begin{aligned}&S(0)>0, \ E(0)\ge 0, \ I_s(0)\ge 0, \ I_a(0)\ge 0, \ Q(0)\ge 0,\\&A(0)>0,\ H(0)\ge 0, \ R(0)\ge 0, \ M(0)\ge M_0. \end{aligned}$$

Here, \(0\le c_{m_s},c_{m_a},a,\theta \le 1\) with \(c_{m_s}\gg c_{m_a}\). That is, the efficacy of social media advertisements to reduce the contacts of susceptibles with symptomatic individuals is comparatively more in comparison to that with the asymptomatic individuals. It may be noted that \(\beta _1\ne \beta _2\), stand for the possible heterogeneity in contact rate in presence or absence of clinical symptoms of COVID-19. For the feasibility of model system (1), we must have \(\beta _1\ge \beta _2\). All the parameters involved in system (1) are assumed to be positive and their description is given in Table 1.

Using the fact that \(N=S+E+I_s+I_a+Q+A+H+R\), the model system (1) reduces to following system of equations:

$$\begin{aligned} \frac{dE}{dt}= & {} \left[ \beta _1\left( 1-c_{m_s}\frac{M}{p+M}\right) I_s+\beta _2\left( 1-c_{m_a}\frac{M}{p+M}\right) I_a\right] (N\nonumber \\&-E-I_s-I_a-Q-A-H-R)-(\sigma +d)E,\nonumber \\ \frac{dI_s}{dt}= & {} (1-a)\sigma E+\beta _a I_a-(\alpha _s+d)I_s-\phi _sI_s,\nonumber \\ \frac{dI_a}{dt}= & {} a\sigma E-\beta _aI_a-\gamma _aI_aM-dI_a,\nonumber \\ \frac{dQ}{dt}= & {} \gamma _aI_a M-\phi _h Q-dQ,\nonumber \\ \frac{dA}{dt}= & {} \lambda M(N-E-I_s-I_a-Q-A-H-R)-(\lambda _0+d)A,\nonumber \\ \frac{dN}{dt}= & {} \varLambda -dN-\alpha _sI_s-\alpha _hH,\nonumber \\ \frac{dH}{dt}= & {} \phi _s I_s-(\nu _h+\alpha _h+d)H,\nonumber \\ \frac{dR}{dt}= & {} \phi _h Q+\nu _h H-(\delta +d)R,\nonumber \\ \frac{dM}{dt}= & {} r\left( 1-\theta \frac{A}{w+A}\right) I_s-r_0(M-M_0). \end{aligned}$$
(2)
Table 1 Descriptions of parameters involved in system (1)
Full size table

The feasible region for system (2) is given in the following lemma [46, 47].

Lemma 1

For the solutions of system (2), the region of attraction is given by the set

$$\begin{aligned} \varOmega= & {} \left\{ (E,I_s,I_a,Q,A,N,H,R,M)\in {\mathbb {R}}^9_+| \ 0\le E,I_s,I_a,Q,A,H,R\le N\le \frac{\varLambda }{d};\right. \\&\left. \quad 0\le M\le M_0+\frac{r\varLambda }{r_0d}\right\} , \end{aligned}$$

which is invariant and compact with respect to system (2).

3 Mathematical analysis of system (2)

3.1 Disease-free equilibrium and basic reproduction number

For model system (2), the disease-free equilibrium is

$$\begin{aligned} E_0=\left( 0,0,0,0,\frac{\lambda \varLambda M_0}{d(\lambda M_0+\lambda _0+d)},\frac{\varLambda }{d},0,0,M_0\right) . \end{aligned}$$

The equilibrium \(E_0\) always exists in the system.

Using the next generation operator method [48], we determine the expression for basic reproduction number. The basic reproduction number, \({\mathcal {R}}_0\), an index worldwide commonly used by public health organization as key estimator of severity of given epidemic.

The new infection terms and transmission terms of system (2) is given by

$$\begin{aligned} {\mathcal {F}}=\left( \begin{array}{c} {\mathcal {F}}_{11}\\ 0\\ 0\\ 0 \end{array}\right) , \ {\mathcal {V}}=\left( \begin{array}{c} (\sigma +d)E\\ -(1-a)\sigma E-\beta _aI_a+(\phi _s+\alpha _s+d)I_s\\ -a\sigma E+(\beta _a+\gamma _a M+d)I_a \end{array}\right) , \end{aligned}$$

where

$$\begin{aligned}&{\mathcal {F}}_{11}=\left[ \beta _1\left( 1-c_{m_s}\frac{M}{p+M}\right) I_s+\beta _2\left( 1-c_{m_a}\frac{M}{p+M}\right) I_a\right] (N\\&\quad -E-I_s-I_a-Q-A-H-R). \end{aligned}$$

Now, we find the matrix F (of new infection terms) and V (of the transition terms) as

$$\begin{aligned} F= & {} \left[ \begin{array}{ccc} 0 &{} \displaystyle \beta _1\left( 1-c_{m_s}\frac{M_0}{p+M_0}\right) \frac{\varLambda }{d}\frac{\lambda _0+d}{\lambda M_0+\lambda _0+d} &{} \displaystyle \beta _2\left( 1-c_{m_a}\frac{M_0}{p+M_0}\right) \frac{\varLambda }{d}\frac{\lambda _0+d}{\lambda M_0+\lambda _0+d}\\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 \end{array}\right] ,\\ V= & {} \left[ \begin{array}{ccc} \sigma +d &{} \ \ 0 &{} 0\\ -(1-a)\sigma &{} \ \ \phi _s+\alpha _s+d &{} -\beta _a\\ -a\sigma &{} \ \ 0 &{} \beta _a+\gamma _aM_0+d \end{array}\right] . \end{aligned}$$

The basic reproduction number is given by \({\mathcal {R}}_0=\rho (FV^{-1})\), where \(\rho \) is the spectral radius of the next generation matrix \(FV^{-1}\). Thus, from the model system (2), we obtain the expression for \({\mathcal {R}}_0\) as

$$\begin{aligned} {\mathcal {R}}_0= & {} \frac{\varLambda }{d}\frac{\lambda _0+d}{(\lambda M_0+\lambda _0+d)(\sigma +d)(\beta _a+\gamma _aM_0+d)}\\&\quad \times \left[ \beta _1\left( 1-c_{m_s}\frac{M_0}{p+M_0}\right) \frac{(1-a)\sigma (\gamma _aM_0+d) +\sigma \beta _a}{\phi _s+\alpha _s+d}\right. \\&\quad \left. +\beta _2a\sigma \left( 1-c_{m_a}\frac{M_0}{p+M_0}\right) \right] . \end{aligned}$$

Following [48], regarding local stability of the disease-free equilibrium \(E_0\) of the system (2), we have the following theorem.

Theorem 1

For system (2), the disease-free equilibrium \(E_0\) is locally asymptotically stable if \({\mathcal {R}}_0<1\) and unstable if \({\mathcal {R}}_0>1\).

3.2 Endemic equilibrium and its global stability

From system (2), an endemic equilibrium is \(E_*=(E^*,I_s^*,I_a^*,Q^*,A^*,N^*,H^*,R^*,M^*)\) whose components are positive solutions of equilibrium equations of system (2).

From the third equilibrium equation of system (2), we have

$$\begin{aligned} E^*=\frac{(\beta _a+\gamma _aM^*+d)I_a^*}{a\sigma }. \end{aligned}$$
(3)

Now, from the second equilibrium equation of system (2) and using Eq. (3), we have

$$\begin{aligned} I_s^*=\frac{(1-a)\sigma (\beta _a+\gamma _aM^*+d)+a\sigma \beta _a}{a\sigma (\phi _s+\alpha _s+d)}I_a^*=f_1(M^*)I_a^*, \end{aligned}$$
(4)

where

$$\begin{aligned} f_1(M^*)=\frac{(1-a)\sigma (\beta _a+\gamma _aM^*+d)+a\sigma \beta _a}{a\sigma (\phi _s+\alpha _s+d)}. \end{aligned}$$

From the fourth equilibrium equation of system (2), we have

$$\begin{aligned} Q^*=\frac{\gamma _aM^*I_a^*}{\phi _h+d}. \end{aligned}$$
(5)

From the seventh equilibrium equation of system (2) and using Eq. (4), we have

$$\begin{aligned} H^*=\frac{\phi _sf_1(M^*)I_a^*}{\nu _h+\alpha _h+d}. \end{aligned}$$
(6)

Further, from the sixth equilibrium equation of system (2) and using Eqs. (4) and (6), we have

$$\begin{aligned} N^*=\frac{\varLambda }{d}-\left( \frac{\alpha _s}{d}+\frac{\alpha _h\phi _s}{\nu _h+\alpha _h+d}\right) f_1(M^*)I_a^*. \end{aligned}$$
(7)

From the eighth equilibrium equation of system (2) and using Eqs. (5) and (6), we have

$$\begin{aligned} R^*=\left[ \frac{\phi _h\gamma _aM^*}{(\delta +d)(\phi _h+d)}+\frac{\nu _h\phi _s f_1(M^*)}{(\delta +d)(\nu _h+\alpha _h+d)}\right] I_a^*. \end{aligned}$$
(8)

Using Eqs. (3)−(8) in the fifth equilibrium equation of system (2), we get

$$\begin{aligned} A^*=\frac{\lambda M^*\{\varLambda -df_2(M^*)I_a^*\}}{d(\lambda M^*+\lambda _0+d)}, \end{aligned}$$
(9)

where

$$\begin{aligned} f_2(M^*)= & {} f_1(M^*)\left( \frac{\alpha _s}{d}+\frac{\alpha _h\phi _s}{\nu _h+\alpha _h+d}\right) +\frac{\beta _a+\gamma _aM^*+d}{a\sigma }+f_1(M^*)\\&+1+\frac{\gamma _aM^*}{\phi _h+d}+\frac{\phi _sf_1(M^*)}{\nu _h+\alpha _h+d}+\frac{\phi _h\gamma _aM^*}{(\delta +d)(\phi _h+d)}\\&+\frac{\nu _h\phi _sf_1(M^*)}{(\delta +d)(\nu _h+\alpha _h+d)}. \end{aligned}$$

Using Eqs. (3)−(9) in the first equilibrium equations of system (2), we have

$$\begin{aligned}&\left[ \beta _1\left( 1-c_{m_s}\frac{M}{p+M}\right) f_1(M)+\beta _2\left( 1-c_{m_a}\frac{M}{p+M}\right) \right] \nonumber \\&\quad \left( \frac{\lambda _0+d}{\lambda M+\lambda _0+d}\right) \left( \frac{\varLambda -df_2(M)I_a}{d}\right) \nonumber \\&\quad -\frac{(\sigma +d)(\beta _a+\gamma _aM+d)}{a\sigma }=0. \end{aligned}$$
(10)

Using Eqs. (4) and (9) in the ninth equilibrium equations of system (2), we have

$$\begin{aligned}&r\left[ \frac{wd(\lambda M+\lambda _0+d)+(1-\theta )\lambda M\{\varLambda -df_2(M)I_a\}}{wd(\lambda M+\lambda _0+d)+\lambda M\{\varLambda -df_2(M)I_a\}}\right] f_1(M)I_a-r_0(M-M_0)\nonumber \\&\quad =0. \end{aligned}$$
(11)

Note that Eqs. (10) and (11) are two isoclines in M and \(I_a\). It is difficult to analyze the behavior of these isoclines mathematically. Let \((I_a^*,M^*)\) be unique point of intersection of isoclines (10) and (11).

Regarding global stability of endemic equilibrium \(E_*\), we have the following theorem [49].

Theorem 2

The endemic equilibrium \(E_*\), if feasible, is globally asymptotically stable inside the region of attraction \(\varOmega \) if the following inequalities are satisfied;

$$\begin{aligned}&\left[ \beta _1\frac{\varLambda }{d}\left( 1-c_{m_s}\frac{M^*}{p+M^*}\right) \right] ^2<\frac{2}{27}\frac{(\phi _s+\alpha _s+d)\pi (\pi +\sigma +d)}{(1-a)\sigma }, \end{aligned}$$
(12)
$$\begin{aligned}&\left[ \beta _2\frac{\varLambda }{d}\left( 1-c_{m_a}\frac{M^*}{p+M^*}\right) \right] ^2<\frac{4}{45}\frac{(\beta _a+d)\pi (\pi +\sigma +d)}{a\sigma },\end{aligned}$$
(13)
$$\begin{aligned}&\frac{\beta _a^2}{(1-a)\sigma }<\frac{2}{15}\frac{(\phi _s+\alpha _s+d)(\beta _a+d)}{a\sigma },\end{aligned}$$
(14)
$$\begin{aligned}&\left[ \frac{\varLambda ^2(\beta _1c_{m_s}+\beta _2c_{m_a})}{d^2(p+M^*)}\right] ^2<\frac{2r_0}{27}(\pi +\sigma +d),\end{aligned}$$
(15)
$$\begin{aligned}&\pi ^2<\frac{1}{9}(\delta +d)(\pi +\sigma +d),\end{aligned}$$
(16)
$$\begin{aligned}&\frac{(\gamma _aI_a^*)^2\pi }{a\sigma }<\frac{2r_0}{15}(\beta _a+d),\end{aligned}$$
(17)
$$\begin{aligned}&r^2\left( 1-\theta \frac{A^*}{w+A^*}\right) ^2<\frac{r_0\pi }{9}\frac{\phi _s+\alpha _s+d}{(1-a)\sigma },\end{aligned}$$
(18)
$$\begin{aligned}&\left( \frac{\phi _h}{\phi _h+d}\right) ^2\max \left\{ \frac{1}{\delta +d},\frac{9\pi ^2}{4\phi _h^2(\pi +\sigma +d)}\right\} \nonumber \\&\quad <\frac{2}{25}\min \left\{ \frac{2}{5}\frac{(\beta _a+d)\pi }{a\sigma \left[ \gamma _a\left( \frac{r\varLambda }{r_0d}+M_0\right) \right] ^2},\frac{1}{3}\frac{r_0}{\gamma _aI_a^*}\right\} ,\end{aligned}$$
(19)
$$\begin{aligned}&\left( \frac{\nu _h}{\nu _h+\alpha _h+d}\right) ^2\max \left\{ \frac{1}{\delta +d},\frac{9\pi ^2}{4\nu _h^2(\pi +\sigma +d)}\right\} <\frac{2}{75}\frac{\pi (\phi _s+\alpha _s+d)}{\phi _s^2(1-a)\sigma },\end{aligned}$$
(20)
$$\begin{aligned}&\frac{\pi ^2}{d(\pi +\sigma +d)}<\frac{1}{9}\min \left\{ \frac{d\pi }{\sigma \alpha _s^2}\frac{\phi _s+\alpha _s+d}{(1-a)\sigma },\frac{dm_6(\nu _h+\alpha _h+d)}{5\alpha _h^2}\right\} ,\end{aligned}$$
(21)
$$\begin{aligned}&\left( \frac{\lambda M^*}{\lambda M^*+\lambda _0+d}\right) ^2\max \left\{ \frac{3\pi ^2}{2(\pi +\sigma +d)},\frac{1}{r_0}\left( \frac{r\theta \varLambda }{d(w+A^*)}\right) ^2\right\} \nonumber \\&\quad <\frac{1}{75}\min \left\{ \frac{r_0}{3}\left( \frac{dM^*}{\varLambda }\right) ^2,\frac{m_5d}{2},\frac{2(\pi +\sigma +d)}{9},\frac{\pi (\phi _s+\alpha _s+d)}{5(1-a)\sigma },\right. \nonumber \\&\quad \left. \frac{2\pi }{5}\frac{\beta _a+d}{a\sigma },\frac{2m_3(\phi _h+d)}{5},\frac{2m_6(\nu _h+\alpha _h+d)}{5},\frac{\delta +d}{2}\right\} , \end{aligned}$$
(22)

where

$$\begin{aligned} \pi =\beta _1\left( 1-c_{m_s}\frac{M^*}{p+M^*}\right) I_s^*+\beta _2\left( 1-c_{m_a}\frac{M^*}{p+M^*}\right) I_a^*. \end{aligned}$$

Proof

Can be easily proved by considering the Lyapunov function

$$\begin{aligned} G= & {} \frac{1}{2}(E-E^*)^2+\frac{m_1}{2}(I_s-I_s^*)^2+\frac{m_2}{2}(I_a-I_a^*)^2+\frac{m_3}{2}(Q-Q^*)^2\nonumber \\&+\frac{m_4}{2}(A-A^*)^2+\frac{m_5}{2}(N-N^*)^2+\frac{m_6}{2}(H-H^*)^2+\frac{m_7}{2}(R-R^*)^2\nonumber \\&+\frac{m_8}{2}(M-M^*)^2, \end{aligned}$$
(23)

where \(m_i\)’s \((i=1-8)\) are positive constants to be chosen appropriately. \(\square \)

4 Numerical simulation

4.1 Model calibration

We have calibrated our model system (1) with the cumulative confirmed COVID-19 cases for the Republic of India. The cumulative confirmed COVID-19 cases are obtained from World Health Organization (WHO) situation report for the period April 01, 2020 to September 07, 2020 [1]. We have estimated eight parameters among 24 model parameters by using sensitivity analysis [50], namely \(\beta _1\), \(\beta _2\), \(\sigma \), \(\lambda \), \(\lambda _0\), \(\alpha _s\), d and \(r_0\) for the system (1) by using least square method. The values of these model parameters and the initial size of the population plays an important role in the model simulation. The parameters are estimated by assuming the initial size of the population. The initial population are as follows:

$$\begin{aligned} S= & {} 1352642280, \ E=5, \ I_s=1, \ I_a=0, \ Q=0, \ A=0, \ H=0, \ R=0, \\&M=2. \end{aligned}$$

Three days moving average filter has been employed to the cumulative confirmed COVID-19 cases to smooth the data. The cumulative confirmed COVID-19 cases are fitted with the model simulation by using the least square method. The estimated parameter values are listed in Table 2. Parameter values locally minimize the Root Mean Square Error (RMSE), which gives the realistic value of the basic reproduction number \({\mathcal {R}}_{0}=4.8273\) and show that the trend of cumulative confirmed COVID-19 cases is increasing. RMSE is the measure of the accuracy of the data fitting and can be defined as

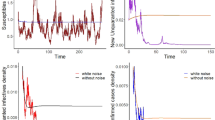
$$\begin{aligned} \begin{aligned} RMSE=\sqrt{\frac{\varSigma _{i=1}^{n} ( O(i)-M(i))^2}{n}}, \end{aligned} \end{aligned}$$

where n represents the size of the observed data, O(i) is the cumulative confirmed COVID-19 cases and M(i) represents the model simulation. Figure 2 represents the cumulative confirmed COVID-19 cases and model simulations has been shown in the blue curve for India. The RMSE for India is 175.65. As \({\mathcal {R}}_{0}>1\), so the disease-free equilibrium point \(E_0\) is unstable. The basic reproduction number for India is greater than unity, which represents the substantial outbreak of the COVID-19 in India.

Table 2 Values of parameters in system (1)
Full size table
Fig. 2
figure 2

Plots of the output of the fitted model (1) and the observed active corona cases for India. Red dotted line shows real data points and the blue line stands for model solution. The figure shows that the cumulative number of COVID-19 increases exponentially as time progresses

Full size image

For parameter values in Table 2, we obtain the components of equilibrium \(E_*\) as

$$\begin{aligned}&E^*=21756250890, \\&I^*_s=39942.43903, \\&I^*_a=0.005426538804, \\&Q^*=132847.3008,\\&A^*=106618625300, \\&N^*=128375356700, \\&H^*=12889.98007, \\&R^*=21778.64515,\\&M^*=797837.0172. \end{aligned}$$

Eigenvalues of the Jacobian matrix of system (2) at the equilibrium \(E_*\) are obtained as

$$\begin{aligned}&-\,9934.0801, \ -\,159567.4178, \ -\,0.0774, \ -\,0.0370, \ -\,0.0545, \\&-\,0.0005\pm 0.0010 i,-\,0.0065, \ -\,0.0045. \end{aligned}$$

Since eigenvalues are either negative or have negative real parts, the equilibrium \(E_*\) is locally asymptotically stable.

Fig. 3
figure 3

Global stability of the endemic equilibrium \(E_*\) of system (1) in a \(I_s\)–\(I_a\)–M and b S–E–R spaces. Parameters are at the same values as in Fig. 8. Figure shows that solution trajectories starting from four different initial points ultimately converge to the components of endemic equilibrium \(E_*\)

Full size image

In Fig. 3a, we have portrayed the global asymptotic stability of the endemic equilibrium \(E_*\) in \(I_s\) \(-\) \(I_a\) \(-\) \(M\) space. The figure depicts that all the solution trajectories of the system (1) originating from four different initial conditions ultimately converge to the point \((I^*_s,I^*_a,M^*)\). The global asymptotic stability of the endemic equilibrium \(E_*\) in \(S\) \(-\) \(E\) \(-\) \(R\) space is shown in Fig. 3b. Using this approach, the global asymptotic stability of the endemic equilibrium \(E_*\) in other spaces can also be extrapolated. Thus, the statement of Theorem 2 is validated numerically.

Fig. 4
figure 4

Semi-relative sensitivities of the symptomatic infected population with respect to model parameters using automatic differentiation. The observation window is [0,400] and the sensitivity of a parameter is identified by the maximum deviation of the state variable (along y-axis) and it also identifies the time intervals when the system is most sensitive to such changes. Parameters are at the same values as in Table 2

Full size image
Fig. 5
figure 5

Sensitivity quantification by calculating sensitivity coefficient through \(L^2\) norm. Ranking of parameters from the most sensitive to the least ones yields the ordering \([\sigma ,r_0,d,\beta _1,\alpha _s,\lambda ,\phi _s,r,\lambda _0]^T\)

Full size image
Fig. 6
figure 6

Normalized forward sensitivity indices of \({\mathcal {R}}_0\) with respect to model parameters. Parameters are at the same values as in Table 2. A lower value of \({\mathcal {R}}_0\) is preferable since it enhances the possibility of disease eradication. Therefore, above all an increase in the parameters \(\varLambda \), \(\beta _1\), \(\sigma \) and \(\lambda _0\) must be prevented by all means, while an increase in \(c_{m_s}\), a, \(\phi _s\), \(\lambda \), \(\alpha _s\), d and \(M_0\) should instead be favored

Full size image

4.2 Sensitivity analysis

Here, we perform sensitivity analysis to identify the most influential parameters concerned with the symptomatic infected population in agreement with the model assumptions. Following [52, 53], we draw sensitivity graphs by using the code myAD (automatic differentiation), Fig. 4. To measure the sensitivity of the model parameters from Fig. 4, we compute the sensitivity coefficients by normalizing the sensitivity functions and deriving the \(L^2\) norm of the resulting functions, obtained by

$$\begin{aligned} C_{ij}= & {} \bigg \Vert \frac{\partial x_i}{\partial q_j}\frac{q_j}{\max x_i}\bigg \Vert ^2_2=\int ^{t_f}_{t_0}\bigg |\frac{\partial x_i}{\partial q_j}\frac{q_j}{\max x_i}\bigg |^2dt. \end{aligned}$$
(24)

Among many identifiability strategies implemented to calibrate the sensitivity coefficients, the easiest strategies imply that the larger the coefficients, the more mastery the model outcome with respect to that parameter. In this case, a parameter with a greater sensitivity is more likely to be identifiable. Since the sensitivity functions are evaluated at some nominal values for the parameters, the analysis is only local. After ranking the sensitivity functions, we categorize the most sensitive parameters (in descending order) to the least ones, Fig. 5. Our case yields the ordering \([\sigma ,r_0,d,\beta _1,\alpha _s,\lambda ,\phi _s,r,\lambda _0]^T\), that is, out of the 24 parameters, only the first nine ranked parameters are the most identifiable and sensitive parameters. Since other parameters are not sensitive, they will not affect the equilibrium number of symptomatic population much. Looking at the identifiable and sensitive parameters, it is worth saying that the intervention strategies must focus on the reductions in the parameters which can trigger the symptomatic population viz. \(\sigma \), \(r_0\), \(\beta _1\) and \(\lambda _0\). Instead, the parameters \(\lambda \), r and \(\phi _s\) should be fostered to reduce the severity of the outbreak significantly. Therefore, awareness programs must be continuously propagated for understanding the pattern of disease transmission. In this way, behavioral changes among susceptible individuals are induced, and hence their rate of contact with the symptomatic infected population will be reduced. Also, the symptomatic infected individuals will be hospitalized immediately.

We also establish the normalized forward sensitivity indices of the basic reproduction number with respect to model parameters [54]. The normalized forward sensitivity index of a variable to a parameter describes the ratio of the relative change in the variable to the relative change in the parameter, i.e., the normalized forward sensitivity index of a variable \(\gamma \) that depends differentiably on a parameter \(\delta \). It is defined as: \(\displaystyle X^\gamma _\delta =\frac{\partial \gamma }{\partial \delta }\times \frac{\delta }{\gamma }.\) In Fig. 6, we plot the sensitivity indices of \({\mathcal {R}}_0\) with respect to the parameters of interest. Evidently, Fig. 6 suggests that the magnitude of \({\mathcal {R}}_0\) increases with increase in the values of parameters \(\varLambda \), \(\beta _1\), \(\sigma \) and \(\lambda _0\) as these parameters possess positive indices with \({\mathcal {R}}_0\). Similarly, the parameters having negative indices with \({\mathcal {R}}_0\) are \(c_{m_s}\), a, \(\phi _s\), \(\lambda \), \(\alpha _s\), d and \(M_0\). Hence, increments in these parameters cause significant decline in the values of \({\mathcal {R}}_0\). We find that the parameters \(\varLambda \), \(\beta _1\) and \(\sigma \) have sensitivity index 1 with \({\mathcal {R}}_0\). It means that 1% increase in the values of these parameters will result in 1% increase in the value of \({\mathcal {R}}_0\). It is clear that achieving a lower value of \({\mathcal {R}}_0\) helps to prevent the disease spread. Thus, to wipe out the disease from the system, we must control the increase of the parameters having positive indices with basic reproduction number whereas parameters which have negative indices should be sustained. Despite these significantly sensitive model parameters associated with the disease transmissibility, the parameters related to social media advertisements can also help to curb the spread of COVID-19. Therefore, Government and health-care officials should adopt practical and effective intervention strategies that can keep potential audience updated about the ongoing health issues and their possible solutions. We find that the control parameters such as dissemination rate of awareness among susceptible individuals, rate of hospitalization of symptomatic individuals, baseline number of social media advertisements etc., which are negatively correlated with \({\mathcal {R}}_0\) should be implemented by means of proper broadcasting of information through social media advertisements and efficient health-care services.

Fig. 7
figure 7

Plots of basic reproduction number (\({\mathcal {R}}_0\)) with respect a \(\lambda \) and \(M_0\), and b \(c_{m_s}\) and \(\phi _s\). Rest of the parameters are at the same values as in Table 2. The figures show that the values of \({\mathcal {R}}_0\) can be maintained below unity by boosting up the parameters \(\lambda \), \(M_0\), \(c_{m_s}\) and \(\phi _s\)

Full size image

4.3 Impacts of some key parameters on disease control

As pointed out in the introduction, now, we are interested to see the impact of broadcasting the information through social media advertisements on disease control. For this, we select four parameters related to social media advertisements and plot the basic reproduction number \({\mathcal {R}}_0\) by varying two parameters at a time viz. \((M_0,\lambda )\) and \((\phi _s,c_{m_s})\) (see Fig. 7). It is apparent from Fig. 7a that the epidemic potential can be drawn below unity for higher values of \(M_0\) and \(\lambda \). That is, increment in the baseline number of social media advertisements and dissemination of awareness due to popularity of new advertisements among susceptible individuals at a higher rate can help to control the spread of coronavirus in India. It can be noted from Fig. 7b that for lower values of \(\phi _s\) and \(c_{m_s}\), \({\mathcal {R}}_0\) becomes greater than one whereas increasing values of these parameters push back the value of \({\mathcal {R}}_0\) to less than unity. This shows the importance of efficacy of awareness programs to reduce the contact rate with symptomatic individuals via propagating awareness among susceptible individuals and the hospitalization of symptomatic individuals in controlling the disease. The public health implication of this is that, COVID-19 can be controlled effectively and will be eventually eradicated from India by social media advertisements which influence the public for compulsory face masks wearing while in public, frequent sanitization, social distancing, hospitalization of symptomatic individuals and quarantine of asymptomatic individuals.

Fig. 8
figure 8

Contour lines representing the equilibrium values of symptomatic individuals (\(I_s\)) as functions of a \(\varLambda \) and \(\beta _1\), b \(\phi _h\) and \(\beta _2\), c r and \(r_0\), d \(\lambda \) and \(\delta \), e \(c_{m_s}\) and p, f \(c_{m_a}\) and p, g \(M_0\) and \(\lambda _0\), h \(\phi _s\) and \(\beta _a\), and i \(\gamma _a\) and \(\theta \). Parameters are at the same values as in Table 2 except \(\varLambda =100\), \(\beta _1=0.000004\), \(\beta _2=0.0000012\), \(\lambda =0.0012\), \(p=1200\), \(\lambda _0=0.008\), \(\sigma =0.19\), \(\gamma _a=0.002\), \(\delta =0.0005\), \(d=0.00003518\), \(r=0.01\), \(r_0=0.005\), \(M_0=500\). The figures clearly indicate that behavioral changes induced by propagation of awareness through social media advertisements can help to reduce the active symptomatic infections effectively

Full size image

Next, we plot the symptomatic infected population by varying two parameters at a time viz. \((\varLambda ,\beta _1)\), \((\phi _h,\beta _2)\), \((r,r_0)\), \((\lambda ,\delta )\), \((c_{m_s},p)\), \((c_{m_a},p)\), \((M_0,\lambda _0)\), \((\phi _s,\beta _a)\) and \((\gamma _a,\theta )\) (see Fig. 8). We see that with increase in the contact rate of susceptible individuals with symptomatic or asymptomatic infected individuals, the symptomatic infections rise up in the region. This shows that in order to control symptomatic infections, attention should be paid on reduction of contact rates of susceptibles with symptomatic and asymptomatic infected individuals, which can be achieved by raising awareness through media programs. It is apparent from the figure that increase in the rate of broadcasting social media advertisements decrease the number of symptomatic population to a low equilibrium value while diminution in the advertisements cause climb in the symptomatic infections. We find that with increase in the dissemination rate of awareness due to popularity of new advertisements among susceptible individuals \(\lambda \), the number of symptomatic infected population decreases. The parameters \(c_{m_s}\) and \(c_{m_a}\) representing the efficacy of social media advertisements in reducing the contacts of susceptibles with symptomatic and asymptomatic individuals respectively, significantly decrease the symptomatic infections. Loss rate of awareness by aware people, \(\lambda _0\), boost up the symptomatic infections, thus this should be prevented. Maintaining the baseline number of awareness \(M_0\), keep the infection at low level. Immediate hospitalization of symptomatic individuals greatly reduces disease prevalence. Increment in the rate of quarantine of asymptomatic individuals, \(\gamma _a\), lessen the number of symptomatic infected population at a very low rate.

Fig. 9
figure 9

Variation of symptomatic individuals (\(I_s\)) with respect to time for different values of a r and \(M_0\), and b \(\phi _s\) and \(\lambda \). Parameters are at the same values as in Fig. 8. The figures show that symptomatic infections can be completely eradicated for higher rates of hospitalization and broadcasting of information through social media advertisements

Full size image

Now, we see the equilibrium level of symptomatic infected population as time progresses, Fig. 9. First, we plot the equilibrium number of symptomatic infected population by picking four different combinations of r and \(M_0\), Fig. 9a. Impact of social media advertisements in reducing the number of symptomatic infected population is apparent from this figure. In the absence of social media advertisements, the symptomatic infected population is at higher equilibrium level with very high initial peak. But, the infective population decrease if social media advertisements come into scenario. The growth rate and baseline number of social media advertisements are found to effectively decrease the symptomatic infected population, driving the equilibrium level of symptomatic infected population to zero if the social media advertisements are continuously broadcasted at higher rates. Figure 9b indicates that raising awareness among susceptible individuals about coronavirus and hospitalizing the symptomatic individuals greatly reduces the symptomatic infections in India. We observe that high rate of hospitalization of symptomatic individuals together with continuous propagation of awareness among susceptible population have potential to suppress the burden of COVID-19 in India.

5 Discussion and conclusion

COVID-19 is now one of the deadliest pandemic in human history and has had tragic consequences affecting millions of people worldwide. In India, the outbreak of coronavirus started on 2nd March 2020 and after that, the cases are on an ever-increasing trajectory. With very high population density, the unavailability of specific medication or vaccine and insufficient information about the transmission mechanisms of the disease makes it extremely difficult to fight against the disease effectively. In such a situation, designing an efficient control strategy is one of the crucial factors to curb the disease spread. In this study, we have proposed a mathematical model to investigate the role of social media advertisements on the control of novel coronavirus pandemic in India to assess the impacts of broadcasting through media coverage and social networking web sites (Facebook, Twitter, WhatsApp and other modes of information propagations including TV, radio, print media) and individuals behavioral responses regarding protective measures. We analyzed our model for the stability of the disease-free and endemic equilibria, and the corresponding results indicate that disease can be eradicated if the basic reproduction number is below unity that can be maintained by broadcasting of information through social media advertisements.

Our proposed model is fitted to the cumulative confirmed COVID-19 cases in India and we estimated eight epidemiologically important parameters. By looking at the estimated parameters, it is observed that the rate of disease transmission is very high in India which basically implies the high infectiousness of the disease. We have also estimated the basic reproduction number to get an overview of this phase of the outbreak. This suggests that the rate of disease transmission needs to be controlled otherwise a large proportion of population will be affected within a short period of time. Results of sensitivity analysis explored the importance of social media advertisements in lowering the disease transmission rate. Further, a comprehensive analysis of the impacts of parameters associated with social media advertisements (efficacy of social media advertisements in reducing the contact rates of susceptibles with symptomatic/asymptomatic individuals, hospitalizations of symptomatic individuals and quarantine of asymptomatic individuals) is performed numerically. Our results suggest that higher intervention efforts are needed to control the disease outbreak within a shorter period of time in India. Our analysis also reveals that the strength of the interventions should be increased over time to eradicate the disease effectively.

The results reported in this paper suggests that publicizing information through social media services can be an important factor in the suppression of disease transmission and may be used as a potential disease control strategy. The level of awareness should be increased and efforts should be made on radical behavioral changes among susceptible individuals in order to completely eradicate the COVID-19 in India. In this context, the public-health authorities and policy makers should have major contributions in monitoring the situation to ensure that intervention strategies are being implemented properly. The targeted population must be vaccinated to stop COVID-19 infection. This will increase immunity to fight against the disease and helps to run the economic activities in efficient ways thereby lessening the economic crisis during the pandemic. Media campaigns should be conducted to develop the awareness of the community to the danger of COVID-19 [36]. After the media reporting about COVID-19, people became aware of the disease threat and started reducing their contacts with others. The Government of India imposed complete countrywide lockdown to flatten the curve of the infection and to reduce social contact, educational institutions arranged online classes, webinars etc. Recently, after successful trail of the vaccine for COVID-19, the Government of India decided to vaccinate the targeted population. For this, vaccination campaigns are being implemented, and most of the people are getting vaccinated. These behaviors overall resulted in reduced contact with others and delayed disease spread, and suppressed the burden of disease. Our findings suggest that to eradicate the coronavirus pandemic in India, continuous propagation of awareness through social media advertisements is needed to encourage people for adopting preventive measures and undertake vaccination. Finally, it is worthy to mention that the results of this study can be used for any future pandemic.