Analyzing on stability of HIV-PI model with general incidence rate

Abstract

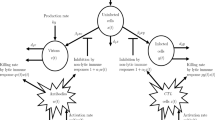
In this article, we have constructed a PI model with general incidence rate and humoral immunity. We have analyzed about the equilibrium points in general case. Using appropriate Lyapunov functional and Lasalle’s invariance principle, the global stability of the newly constructed model have been discussed. Using patient data we have discussed about the model numerically.

Appendix A

Now we consider the Lyapunov functional of the form,

$$\begin{aligned} W (t)= & {} W_{T^*}(t) + e^{m_1 \tau _1} I^* H \left( \frac{I(t)}{I^*} \right) + e^{m_1 \tau _1 + m_2 \tau _2} {V_I}^* H\\&\times \left( \frac{V_I(t)}{{V_I}^*} \right) + e^{m_1 \tau _1 + m_2 \tau _2} {V_{NI}}^* H \left( \frac{V_{NI}(t)}{{V_{NI}}^*} \right) \\&+\, \frac{q}{g} e^{m_1 \tau _1 + m_2 \tau _2} B(t)+ \int \limits _{t - \tau _1}^{t} \left[ f(T^*,V^*) V^* H \left( \dfrac{f(T(\theta ), V(\theta ))V(\theta )}{f(T^*,V^*)V^*} \right) \right] d \theta \\&+\, N \delta e^{m_1 \tau _1} \int \limits _{t - \tau _2}^{t} \left[ I^* H \left( \dfrac{I(\theta )}{I^*} \right) \right] , \end{aligned}$$

where

$$\begin{aligned} H(x) = x - 1 - \text{ ln } x, \end{aligned}$$

and

$$\begin{aligned} W_{T^*}(t) = T(t) - T^* - \int \limits _{T^*}^{T} \dfrac{f(T^*,V^*)}{f(s,V^*)} ds. \end{aligned}$$

Then the derivative of the Lyapunov functional is,

$$\begin{aligned} W ' (t) =&\left( 1- \frac{f(T^*,{V_I}^*)}{f(T(t),{V_I}^*)} \right) T'(t) + e^{m_1 \tau _1} \left( 1 - \frac{I^*}{I(t)} \right) I'(t) \\&+\, e^{m_1 \tau _1+m_2 \tau _2} \left( 1 - \frac{{V_I}^*}{{V_I}(t)} \right) {V_I}'(t)\\&+\, e^{m_1 \tau _1+m_2 \tau _2} \left( 1 - \frac{{V_{NI}}^*}{{V_{NI}}(t)} \right) {V_{NI}}'(t) + \frac{q}{g} e^{m_1 \tau _1+m_2 \tau _2} B'(t) \\&+\, f(T^*,{V_I}^*){V_I}^* H\left( \frac{f(T(t),V_I(t))V_I(t)}{f(T^*,{V_I}^*) {V_I}^*} \right) \\&-\, f(T^*,{V_I}^*){V_I}^* H\left( \frac{f(T(t-\tau _1),V_I(t-\tau _1))V_I(t-\tau _1)}{f(T^*,{V_I}^*) {V_I}^*} \right) \\&+\,e^{m_2 \tau _2} I^* H \left( \frac{I(t)}{I^*} \right) \\&-\, N \delta e^{m_1 \tau _1} I^* H\left( \frac{I(t - \tau _2)}{I^*}\right) , \end{aligned}$$

$$\begin{aligned} =&\left( 1 - \frac{f(T^*,{V_I}^*)}{f(T(t),{V_I}^*)}\right) [s - d_T T(t)- f(T(t),V_I(t))V_I(t)] \\&+\, e^{m_1 \tau _1} \left( 1 - \frac{I^*}{I(t)} \right) [e^{-m_1 \tau _1} f(T(t-\tau _1), V_I(t - \tau _1)) V_I(t - \tau _1) -\delta I(t)] \\&+\, e^{m_1 \tau _1 +m_2 \tau _2} \left( 1 - \frac{{V_I}^*}{V_I(t)}\right) [e^{-m_2 \tau _2} (1 - \epsilon _p) N \delta I(t - \tau _2) -c V_I(t) - q B(t) V_I(t)]\\&+\, e^{m_1 \tau _1 +m_2 \tau _2} \left( 1 - \frac{{V_{NI}}^*}{V_{NI}(t)}\right) [e^{-m_2 \tau _2} \epsilon _p N \delta I(t - \tau _2) -c V_{NI}(t) - q B(t) V_{NI}(t)] \\&+\, \frac{q}{g} e^{m_1 \tau _1 +m_2 \tau _2} [g B(t) V_I (t) + g B(t) V_{NI}(t) -r B(t)] + f(T(t),V_I(t))V_I(t) \\&-\, f(T^*,{V_I}^*){V_I}^* \; \text{ ln } \left( \frac{f(T(t), V_I(t)) V_I(t)}{f(T^*,{V_I}^*){V_I}^* }\right) - f(T(t-\tau _1), V_I(t - \tau _1)) V_I(t - \tau _1) \\&+\, f(T^*,{V_I}^*){V_I}^* \; \ln \left( \frac{f(T(t - \tau _1), V_I(t- \tau _1)) V_I(t - \tau _1)}{f(T^*,{V_I}^*){V_I}^* }\right) \\&+\, e^{m_2 \tau _2} I(t) -e^{m_2 \tau _2} I(t-\tau _2) - e^{m_1 \tau _1} \ln \left( \frac{I(t)}{I^*} \right) + N \delta e^{m_1 \tau _1} \ln \left( \frac{I(t- \tau _2)}{I^*} \right) , \end{aligned}$$

$$\begin{aligned} =&d_T [T^* - T]\left( 1 - \frac{f(T^*,{V_I}^*)}{f(T(t),{V_I}^*)}\right) + f(T^*,{V_I}^*){V_I}^* - f(T(t),V_I(t))V_I(t) \\&-\, f(T^*,{V_I}^*){V_I}^* \left( \frac{f(T^*,{V_I}^*)}{f(T(t),{V_I}^*)}\right) + f(T(t),V_I(t)) V_I(t) \left( \frac{f(T^*,{V_I}^*)}{f(T(t),{V_I}^*)}\right) \\&f(T(t- \tau _1), V_I(t- \tau _1))V_I(t-\tau _1) - \left( \frac{I^*}{I(T)} \right) f(T(t- \tau _1), V_I(t- \tau _1))V_I(t-\tau _1)\\&-\,\delta e^{m_1 \tau _1} I(t) + \delta e^{m_1 \tau _1} I*- \epsilon _p N \delta e^{m_1 \tau _1} I(t-\tau _2) +N \delta e^{m_1 \tau _1} I(t - \tau _2) \\&- e^{m_1 \tau _1} N \delta (1 - \epsilon _p) \left( \frac{{V_I}^*}{V_I (t)}\right) I(t - \tau _2) - c e^{m_1 \tau _1 +m_2 \tau _2} V_I (t) + c e^{m_1 \tau _1 +m_2 \tau _2} {V_I}^* \\&-\, q e^{m_1 \tau _1 +m_2 \tau _2} B(t) V_I(t) + q e^{m_1 \tau _1 +m_2 \tau _2} B(t) {V_I}^* + \epsilon N \delta e^{m_1 \tau _1} I(t - \tau _2) \\&- N \delta \epsilon _p e^{m_1 \tau _1} \left( \frac{{V_{NI}}^*}{V_{NI}} \right) I(t - \tau _2) - c e^{m_1 \tau _1 +m_2 \tau _2} V_{NI} + c e^{m_1 \tau _1 +m_2 \tau _2} {V_{NI}}^* \\&-\, q e^{m_1 \tau _1 +m_2 \tau _2} B(t) V_{NI}(t) + q e^{m_1 \tau _1 +m_2 \tau _2} B(t) {V_{NI}}^* + q e^{m_1 \tau _1 +m_2 \tau _2} B(t) V_I(t) \\&+\, q e^{m_1 \tau _1 +m_2 \tau _2} B(t) V_{NI} (t) - \frac{r}{g} e^{m_1 \tau _1 +m_2 \tau _2} B(t) + f(T(t), V_I(t)) V_I(t) \\&-T(t- \tau _1),V_I(t- \tau _1)) V_I(t- \tau _1) + N \delta e^{m_1 \tau _1} I(t) - N \delta e^{m_1 \tau _1} I(t - \tau _2) \\&- f(T^*, {V_I}^*) {V_I}^* \ln \left( \frac{f(T(t),V_I(t)) V_I(t)}{f(T(t- \tau _1),V_I(t- \tau _1)) V_I(t- \tau _1)} \right) \\&- N \delta e^{m_1 \tau _1} \ln \left( \frac{I(t)}{I(t - \tau _2} \right) . \end{aligned}$$

Since,

• (i) $f(T^*,{V_I}^*){V_I}^* = \delta e^{m_1 \tau _1} I^* = \dfrac{c e^{m_1 \tau _1 + m_2 \tau _2}}{N \epsilon _p} {V_I}^*$,

• (ii) f(T, V) is strictly monotonically increasing with respect to T,

• (iii) f(T, V) is strictly monotonically decreasing with respect to V, and

• (iv) f(T, V)V is monotonically increasing with respect to V,

from the above discussion we get $W'(t)\le 0$. Clearly $W(t) =0$ iff $T=T^*,I=I^*, V_I = {V_I}^*$ and $V_{NI} = {V_{NI}}^*$. Let $M_1$ be the largest invarient subspace of $\{(T,I,V_I,V_{NI},B)| W'=0\}$. For each point in $M_1$, we have $V_I ' =0, V_{NI}' = 0$ and $B = 0$, so $M_1$ includes a unique point, the equilibrium $E_1$. By using Lasalle’s invariance principle, $E_1$ is globally asymptotically stable.