Skip to main content
SpringerLink
Log in

Boundary control of nonlinear elastic systems

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

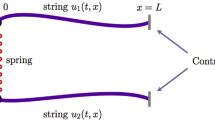
This paper presents a design of boundary controllers for global stabilization of nonlinear elastic systems, which cover nonlinear elastic strings and membranes, under external bounded forces. The boundary controllers guarantee exponential convergence of the unique system solution to a ball centered at the origin. The Faedo–Galerkin approximation method is used to prove existence and uniqueness of the solution of the closed-loop system. The control design is based on the Lyapunov direct method, Gronwall’s, Poincare’s, and Holder’s inequalities, and Sobolev embedding theorems. Simulations illustrate the effectiveness of the proposed controllers.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Ono, K.: Global existence, decay, and blow up of solutions for some mldly degenerate nonlinear Kirchhoff strings. J. Differ. Equ. 137, 273–301 (1997)

    Article  MATH  Google Scholar 

  2. Arosio, A., Panizzi, S.: On the well-posedness of the Kirchhoff string. Trans. Am. Math. Soc. 348(1), 305–330 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  3. Berrimi, S., Messaoudi, S.A.: Exponential decay of solutions to a viscoelastic equation with nonlinear localized damping. Electron. J. Differ. Equ. 88, 1–10 (2004)

    MathSciNet  MATH  Google Scholar 

  4. Cavalcanti, M.M., Cavalcanti, V.N.D., Soriano, J.A.: Exponential decay for the solution of semilinear viscoelastic wave equations with localized damping. Electron. J. Differ. Equ. 44, 1–14 (2002)

    MathSciNet  MATH  Google Scholar 

  5. Alves, C.O., Cavalcanti, M.M.: On existence, uniform decay rates and blow up for solutions of the 2-d wave equation with exponential source. Calc. Var. Part. Differ. Equ. 34, 377–411 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  6. Aassila, M., Cavalcanti, M.M., Soriano, J.A.: Asymptotic stability and energy decay rates for solutions of the wave equation with memory in a star-shaped domain. SIAM J. Control Optim. 38, 1581–1602 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  7. Anderson, B.D.O., Moore, J.B.: Optimal Control: Linear Quadratic Methods. Dover Publications, Mineola (1990)

    MATH  Google Scholar 

  8. Krstic, M., Kanellakopoulos, I., Kokotovic, P.: Nonlinear and Adaptive Control Design. Wiley, New York (1995)

    MATH  Google Scholar 

  9. Khalil, H.: Nonlinear Systems. Prentice Hall, Upper Saddle River (2002)

    MATH  Google Scholar 

  10. Balas, M.J.: Active control of flexible systems. In: Proceeding of the AIAA Symposium on Dynamic and Control of Large Flexible Spacecraft, vol. 23, pp. 217–236. (1977)

  11. Balas, M.J.: Feedback control of flexible systems. IEEE Trans. Autom. Control 23(4), 673–679 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  12. Meirovitch, L.: Principles and Techniques of Vibrations. Prentice-Hall, Upper Saddle River (1997)

    Google Scholar 

  13. Ge, S.S., Lee, T.H., Zhu, G.: A nonlinear feedback controller for a single-link flexible manipulator based on a finite element model. J. Robot. Syst. 14(3), 165–178 (1997)

    Article  MATH  Google Scholar 

  14. Gawronski, W.: Dynamics and Control of Structures a Modal Approach. Springer, New York (1998)

    Book  MATH  Google Scholar 

  15. Ravindran, S.: A reduced-order approach for optimal control of fluids using proper orthogonal decomposition. Int. J. Numer. Methods Fluids 34(5), 425–448 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  16. Lyapunov, A.M.: Stability of Motion. Academic Press, New York (1966)

    MATH  Google Scholar 

  17. Shahruz, S.M.: Boundary control of the axially moving Kirchhoff string. Automatica 34, 1273–1277 (1998)

    Article  MATH  Google Scholar 

  18. Yang, K.-J., Hong, K.-S., Matsuno, F.: Robust adaptive boundary control of an axially moving string under a spatiotemporally varying tension. J. Sound Vib. 273, 1007–1029 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  19. Fung, R.F., Wu, J.M., Wu, S.L.: Stabilization of an axially moving string by nonlinear boundary feedback. J. Dyn. Syst. Meas. Control 121, 117–121 (1999)

    Article  MATH  Google Scholar 

  20. Fung, R.F., Tseng, C.C.: Boundary control of an axially moving string via Lyapunov method. J. Dyn. Syst. Meas. Control 121, 105–110 (1999)

    Article  Google Scholar 

  21. Queiroz, M.S.D., Dawson, M., Nagarkatti, S., Zhang, F.: Lyapunov-Based Control of Mechanical Systems. Birkhauser, Boston (2000)

    Book  MATH  Google Scholar 

  22. Liu, K., Liu, Z.: Boundary stabilization of a nonhomogeneous beam with rotatory inertia at the tip. J. Comput. Appl. Math. 114, 1–10 (2000)

    MathSciNet  MATH  Google Scholar 

  23. Fard, M.P., Sagatun, S.I.: Exponential stabilization of a transversely vibrating beam by boundary control via Lyapunov’s direct method. J. Dyn. Syst. Meas. Control 123, 195–200 (2001)

    Article  MATH  Google Scholar 

  24. Tanaka, N., Iwamoto, H.: Active boundary control of an Euler–Bernoulli beam for generating vibration-free state. J. Sound Vib. 340, 570–586 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  25. Do, K.D., Pan, J.: Boundary control of transverse motion of marine risers with actuator dynamics. J. Sound Vib. 318(4–5), 768–791 (2008)

    Article  Google Scholar 

  26. Do, K.D., Pan, J.: Boundary control of three-dimensional inextensible marine risers. J. Sound Vib. 327(3–5), 299–321 (2009)

    Article  Google Scholar 

  27. Ge, S.S., He, W., How, B.V., Choo, Y.S.: Boundary control of a coupled nonlinear flexible marine riser. IEEE Trans. Control Syst.Technol. 18(5), 1080–1091 (2010)

    Article  Google Scholar 

  28. Do, K.D.: Global stabilization of three-dimensional flexible marine risers by boundary control. Ocean Syst. Eng. 1(2), 171–194 (2011)

    Article  MathSciNet  Google Scholar 

  29. He, W., Ge, S.S., How, B.V., Choo, Y.S., Hong, K.S.: Robust adaptive boundary control of a flexible marine riser with vessel dynamics. Automatica 47(4), 722–732 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  30. Nguyen, T.L., Do, K.D., Pan, J.: Boundary control of marine risers with bending couplings. In: Proceedings of the 12th International Conference on Control, Automation and Systems, pp. 1615–1620 (2012)

  31. Nguyen, T.L., Do, K.D., Pan, J.: Boundary control of coupled nonlinear three dimensional marine risers. J. Mar. Sci. Appl. 12(1), 72–88 (2013)

    Article  Google Scholar 

  32. Nguyen, T.L., Do, K.D., Pan, J.: Boundary control of two-dimensional marine risers with bending couplings. J. Sound Vib. 332(16), 3605–3622 (2013)

    Article  Google Scholar 

  33. Krstic, M., Siranosian, A.A., Balogh, A., Guo, B.-Z.: Control of strings and flexible beams by backstepping boundary control. American Control Conference, New York, pp. 882–887 (2007)

  34. Krstic, M., Siranosian, A.A., Smyshlyaev, A.: Backstepping boundary controllers and observers for the slender timoshenko beam: Part idesign. In: American Control Conference, Minnesota, pp. 2412–2417 (2006)

  35. Krstic, M., Siranosian, A.A., Smyshlyaev, A., Bement, M.: Backstepping boundary controllers and observers for the slender timoshenko beam: Part ii-stability and simulations. In: Proceedings of the 45th IEEE Conference on Decision & Control, pp. 3938–3943 (2006)

  36. Liu, W.J.: Boundary feedback stabilization of an unstable heat equation. SIAM J. Control Optim. 42(3), 1033–1043 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  37. Evans, L.: Partial Differential Equations. American Mathematical Society, Providence (2000)

    Google Scholar 

  38. Adams, R.A., Fournier, J.J.F.: Sobolev Spaces, 2nd edn. Academic Press, Oxford (2003)

    MATH  Google Scholar 

  39. Richtmyer, R.D., Morton, K.W.: Difference Methods for Initial-Value Problems. Wiley, New York (1967)

    MATH  Google Scholar 

  40. Do, K.D.: Hamilton-Jacobi equation for optimal control of nonlinear stochastic distributed parameter systems applied to air pollution process. Appl. Math. Sci. 8(57), 2801–2816 (2014)

    MathSciNet  Google Scholar 

  41. Do, K.D.: Global inverse optimal stabilization of stochastic nonholonomic systems. Syst. Control Lett. 75, 41–55 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  42. Do, K.D.: Global Path-Following Control of Underactuated Ships Under Deterministic and stochastic sea Loads. Robotica, In Press, Cambridge (2015)

    Google Scholar 

  43. Simon, J.: Compact sets in the space \({L^p(0, T;B)}\). Ann. Mat. Pura Appl. 146(1), 65–96 (1986)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Curtin University, Kent Street, Bentley, WA, 6102, Australia

    K. D. Do

Authors
  1. K. D. Do
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to K. D. Do.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Do, K.D. Boundary control of nonlinear elastic systems. J. Appl. Math. Comput. 51, 315–339 (2016). https://doi.org/10.1007/s12190-015-0907-5

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-015-0907-5

Keywords

Mathematics Subject Classification

Search

Navigation