1 Introduction

Recently, research on shale reservoirs has become more important in China (Liu et al. 2009; Liu et al. 2011; Zou et al. 2011; Cheng et al. 2013; Chen et al. 2013a; Chen et al. 2013b; Diao 2013; Wang et al. 2013). However, exploration and exploitation of shale reservoirs requires deeper understanding of rock physics relations between reservoir properties and elastic parameters in shales. Compared to rock physics models for conventional reservoirs (Bai et al. 2012; Zhang et al. 2013; Chen et al. 2014), rock physics methods for shales are primarily focusing on the modeling of shale anisotropy resulting from preferred orientations of clay minerals and pores in shale rock matrix (Vernik and Nur 1992; Hornby et al. 1994; Carcione 2000; Wenk et al. 2007; Bobko and Ulm 2008; Lonardelli et al. 2007; Ortega et al. 2009; Dewhurst et al. 2011; Slatt and Abousleiman 2011). Recently, the impact of kerogen on elastic properties and seismic responses of shales has received more interest. Carcione et al. (2011) and Vernik and Milovac (2011) researched and compared rock physics models for organic-rich shales. Zou et al. (2011) analyzed the capacity of reservoirs in terms of nano-porosity in kerogen in shales. Zhu et al. (2012) improved rock physics models for shale gas reservoirs. Sayers (2013b) calculated the effect of kerogen on anisotropy of shales. Zhu et al. (2011) and Sayers (2013a) studied seismic AVO responses based on the proposed rock physics models for shale. Meanwhile, Sun et al. (2013) modeled seismic responses of shale gas reservoirs based on anisotropic wave equations. However, the effect of kerogen content and kerogen porosity on elastic properties and seismic responses of shale has not been well investigated. According to the observations from SEM images, kerogen plays a more significant role in elastic properties than ever expected due to its low density (Passey et al. 2010); moreover, hydrocarbon-filled pores in such organic matter generated during different maturity levels will enhance the effect of kerogen. Therefore, key parameters for the characterization of organic-rich shales should include both kerogen content and kerogen porosity. In this study, our objective is to build a rock physics workflow for the organic-rich shales to quantify the effects of such two factors on elastic properties, and therefore on the seismic responses.

2 Microstructural model of shale

SEM images reveal the presence of a nano-porosity system contained within the organic matter (Passey et al. 2010). It is estimated that these pores comprise the majority of the total porosity space and may be hydrocarbon saturated during most of the thermal maturation processes. The schematics in Fig. 1 illustrate how 5 wt% (weight percentage) solid kerogen in Fig. 1a may correspond to 10 vol% (volume percentage) solid kerogen in Fig. 1b because the density of kerogen is about half that of average rock minerals, and then may eventually take up 20 vol% in a shale rock in Fig. 1c if 50 % of the organic matter volume is occupied by hydrocarbon-saturated pores. Therefore, a small amount of kerogen in weight percentage corresponds to a relevant higher volume percentage which has a significant impact on elastic properties and seismic responses of shales. The objective of this study is to build a rock physics model for organic-rich shales to quantify the effect of kerogen content and kerogen porosity.

Fig. 1
figure 1

Schematics demonstrate 5 wt% solid kerogen in (a) corresponds to 10 vol% kerogen in (b) due to the lower density of kerogen compared to that of average minerals in the rock matrix, and the generation of hydrocarbon-filled pores during different maturity levels results in the expansion of the volumetric fraction of the mixture of kerogen and hydrocarbons and may take up 20 vol% if half of the spaces are occupied by pores in kerogen as shown in (c). (After Passey et al. 2010)

Full size image

Figure 2 illustrates the evolution of solid and fluid constituents in a source rock associated with various maturity levels. For an immature source rock, kerogen has no pores generated inside (Scenario A). As the source rock becomes mature, hydrocarbon-filled pores are generated in organic matter (Scenario B). In addition, the kerogen content in source rock may be different (Scenario C), and as the source rock becomes more mature, more hydrocarbon-filled pores will be generated in organic matter (Scenario D). According to the above analysis, kerogen content and porosity associated with hydrocarbon-filled pores in kerogen are two important factors for the characterization of a source rock, so we define the two factors as K and φ k, respectively, in this work.

Fig. 2
figure 2

Schematics illustrate the evolution of solid and fluid constituents in a source rock associated with different maturity levels. Scenario A illustrates an immature source rock with no pores generated in kerogen. Scenario B demonstrates a mature source rock with hydrocarbon-filled pores generated in kerogen. In addition, the kerogen content K in a source rock may be different as shown in Scenario C, and hydrocarbon-filled porosity φ k may also vary as shown in Scenario D

Full size image

3 Rock physics workflow for organic-rich shales

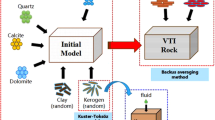
Figure 3 illustrates a rock physics workflow we built to qualify the effect of K and φ k on elastic properties of the organic-rich shale. In the rock physics model, the mixture of kerogen and hydrocarbon-filled pores has non-zero shear modulus (Passey et al. 1990), and the elastic properties of such a mixture are calculated using the method proposed by Carcione (2000) based on the theory of Kuster and Toksöz (1974). After that, the elastic properties of the shale consisting of clay and non-clay minerals, the mixture of kerogen and hydrocarbons, and fluid-saturated pores in the shale rock matrix are calculated using the self-consistent approximation (SCA) method given by Berryman (1980). The constructed rock physics model is based on isotropic assumption and focuses on quantifying the effect of kerogen on elastic properties of shales. The results model the elastic parameters of shales in the vertical direction (one-dimensional problem) and can be applied to analyze the relation between kerogen and elastic properties in a vertical well.

Fig. 3
figure 3

A schematic illustrates the shale rock physics workflow to model the effect of kerogen content and kerogen porosity. Effective medium theories are employed in the workflow

Full size image

As indicated in Fig. 4, we consider that the kerogen/oil/gas/water mixture is composed of oil/gas/water bubbles embedded in a kerogen matrix. The saturations are S k, S o, S g, and S w for kerogen, oil, gas, and water, respectively, and we have S k + S o + S g + S w = 1. We define the kerogen-related porosity as φ k = S o + S g + S w, which is the proportion of the oil/gas/water bubbles in the mixture. The bulk modulus K ogw of the oil/gas/water mixture is obtained by using Wood’s equation (Wood 1955):

$$ \frac{{S_{\text{o}} + S_{\text{g}} + S_{\text{w}} }}{{K_{\text{ogw}} }} = \frac{{S_{\text{o}} }}{{K_{\text{o}} }} + \frac{{S_{\text{g}} }}{{K_{\text{g}} }} + \frac{{S_{\text{w}} }}{{K_{\text{w}} }}, $$
(1)

where K o, K g, and K w are the moduli of oil, gas, and water, and are calculated by

$$ K_{\text{o}} = \rho_{\text{o}} V_{\text{o}}^{2} ,\;\;\;K_{\text{g}} = \rho_{\text{g}} V_{\text{g}}^{2} ,\;\;\;K_{\text{w}} = \rho_{\text{w}} V_{\text{w}}^{2} . $$
(2)
Fig. 4
figure 4

A schematic indicates the mixture of kerogen, oil, gas, and water, and the relationship of the associated saturations

Full size image

Then, the stiffnesses of the mixtures of kerogen and gas/oil/water can be calculated by using the method of Kuster and Toksöz (1974):

$$ \frac{{c_{13}^{{({\text{m}})}} + \frac{2}{3}c_{55}^{{({\text{m}})}} }}{{K_{\text{k}} }} = \frac{{1 + [{{4\mu_{\text{k}} (K_{\text{ogw}} - K_{\text{k}} )} \mathord{\left/ {\vphantom {{4\mu_{\text{k}} (K_{\text{ogw}} - K_{\text{k}} )} {(3K_{\text{ogw}} + 4\mu_{\text{k}} )K_{\text{k}} }}} \right. \kern-0pt} {(3K_{\text{ogw}} + 4\mu_{\text{k}} )K_{\text{k}} }}]\varphi_{\text{k}} }}{{1 - [{{3(K_{\text{ogw}} - K_{\text{k}} )} \mathord{\left/ {\vphantom {{3(K_{\text{ogw}} - K_{\text{k}} )} {(3K_{\text{ogw}} + 4\mu_{\text{k}} )}}} \right. \kern-0pt} {(3K_{\text{ogw}} + 4\mu_{\text{k}} )}}]\varphi_{\text{k}} }}, $$
(3)
$$ \frac{{c_{55}^{{({\text{m}})}} }}{{\mu_{\text{k}} }} = \frac{{(1 - \varphi_{\text{k}} )(9K_{\text{k}} + 8\mu_{\text{k}} )}}{{9K_{\text{k}} + 8\mu_{\text{k}} + s(6K_{\text{k}} + 12\mu_{\text{k}} )}}, $$
(4)

where the superscript m indicates the mixture, K k and μ k are the bulk and shear moduli of kerogen, and φ k is the kerogen porosity. Equations (3) and (4) are used for the solutions of c 13 and c 55, which are two components in the stiffness matrix c ij (i, j = 1, 2,…, 6), and c 13 = c 11−2c 55, c 11 for P-wave in the horizontal direction, and c 55 for S-wave in the vertical direction.

By solving Eqs. (3) and (4), bulk and shear moduli of the mixture of kerogen and gas/oil/water can be obtained by \( K^{{({\text{m}})}} = c_{13}^{{({\text{m}})}} + 2c_{55}^{{({\text{m}})}} /3 \) and \( \mu^{{({\text{m}})}} = c_{55}^{{({\text{m}})}} \). The superscript m denotes the mixture of kerogen/oil/gas/water. Given the density of kerogen (ρ k), oil (ρ o), gas (ρ g), and water (ρ w), the density of the mixture is ρ (m) = S k ρ k + S o ρ o + S g ρ g + S w ρ w.

After obtaining the elastic properties of the kerogen and gas/oil/water mixture, we employ the self-consistent approximation (SCA) method to calculate the bulk and shear moduli of the shale rock. The shale is composed of quartz, clay, carbonate, the mixture of kerogen and hydrocarbons, and fluid-saturated pores in the shale rock matrix. Elastic properties of the constituents and oil, gas, and water are given in Table 1 (Carcione et al. 2011; Mavko et al. 2009).

Table 1 Material properties (Carcione 2000; Mavko et al. 2009)
Full size table

The SCA method estimates the self-consistent elastic modulus \( K_{\text{SC}}^{*} \) and \( \mu_{\text{SC}}^{*} \) of rocks for a given n phases of mineralogy and pore space:

$$ \sum\limits_{j = 1}^{n} {f_{j} \left( {K_{j} - K_{\text{SC}}^{ *} } \right)\beta^{ *j} = 0} , $$
(5)
$$ \sum\limits_{j = 1}^{n} {f_{j} \left( {\mu_{j} - \mu_{\text{SC}}^{ *} } \right)\zeta^{ *j} = 0} . $$
(6)

Each j indicates a phase of mineralogy or pore space with a corresponding volume fraction f j , and bulk (K j ) and shear (μ j ) modulus. The factors β *j and ζ *j describe the geometry of an inclusion made of phase j within a background medium (denoted with subscript b), and are given as follows:

$$ \beta^{*j} = \frac{{K_{b} + \frac{4}{3}\mu_{j} }}{{K_{j} + \frac{4}{3}\mu_{j} + \pi \alpha \mu_{b} \frac{{3K_{b} + \mu_{b} }}{{3K_{b} + 4\mu_{b} }}}}, $$
(7)

and

$$ \xi^{*j} = \frac{1}{5}\left[ {\frac{{8\mu_{b} }}{{4\mu_{j} + \pi \alpha \mu_{b} \left( {1 + 2\frac{{3K_{b} + \mu_{b} }}{{3K_{b} + 4\mu_{b} }}} \right)}} + 2\frac{{K_{j} + \frac{2}{3}\left( {\mu_{j} + \mu_{b} } \right)}}{{K_{j} + \frac{4}{3}\mu_{j} + \pi \alpha \mu_{b} \frac{{3K_{b} + \mu_{b} }}{{3K_{b} + 4\mu_{b} }}}}} \right]. $$
(8)

The implementation of Eqs. (5)–(8) requires volumetric percentage, bulk and shear modulus, and aspect ratio for each inclusion, and the outputs are bulk and shear modulus of rocks. For each inclusion j, background medium b corresponds to the inclusion other than j. Equations (5) and (6) are coupled, and therefore need to be solved by a simultaneous iteration method. Equations (7) and (8) represent the geometries of pores with aspect ratio smaller than 1 (Mavko et al. 2009).

4 The effect of K and φ k on elastic and geo-mechanical properties

According to the observations and analysis by Passey et al. 1990, constituents of the organic-rich shale consist of clay, quartz, dolomite, hydrocarbon-saturated kerogen, and fluid-saturated pores in shale matrix. In the rock physics modeling, we set the mineralogical volumetric contents of clay and dolomite to 0.3 and 0.15, respectively, and the porosity associated with shale matrix is 0.05. We assume the contents of kerogen and quartz have a negative correlation, that is, an increase in kerogen content K corresponds to a decrease in quartz content. So, if K increases from 0 to 0.3, quartz content decreases from 0.5 to 0.2 correspondingly. Associated elastic properties are given in Table 1. For the constituents in shales, in this study, n in Eqs. (5)–(8) corresponds to n = 5.

We assume the pores in kerogen are totally gas saturated to imitate high maturity level, and the pores in shale matrix are water saturated. Another key factor is the aspect ratio of the pores in the shale matrix, and we set it as 0.1 according to the study on the Barnett Shale (Guo et al. 2013a, b). According to the work on shale rock physics by Carcione (2000), we assume spherical geometry of pores in kerogen.

Then based on the rock physics model in Fig. 3 and properties in Table 1, we calculate elastic and geo-mechanical properties of the organic-rich shale along with the variations in kerogen content K and kerogen-related porosity φ k. Figure 5a, b, and c illustrate the obtained P- and S-wave velocity V p, and V s, and density ρ of the shale for varied kerogen content K and kerogen porosity φ k. We can see that the values of V p, V s, and ρ decrease significantly as K increases from 0 to 0.3 and φ k from 0 to 0.5. For example, V p has a value about 3370 km/s for K = 0.1 and φ k = 0.1, and this value decreases to 2783 km/s for K = 0.2 and φ k = 0.2.

Fig. 5
figure 5

Calculated templates showing a P-wave velocity V p, b S-wave velocity V s, and c Density ρ for the variations in kerogen content K and kerogen-related porosity φ k in the shale

Full size image

We also find the correlation between the effect of K and that of φ k on elastic properties, which impact elastic properties of shale simultaneously. Due to low velocities and density, the increase in K decreases velocities and density, and the presence of φ k enhances such impacts (as shown in Fig. 1). For K < 0.05, the effect of φ k on the elastic properties is not obvious; for K > 0.05, the increase in φ k significantly decreases velocities and density of shales.

Figure 6a and b illustrate the calculated Young’s modulus E and Poisson’s ratio v for the same range of K and φ k as those in Fig. 5 (Zong et al. 2012). The two geo-mechanical properties are critical for the evaluation of the brittleness index of shales, as higher E and lower v indicate higher potential for shales to be fractured during hydraulic stimulation (Rickman et al. 2008). In Fig. 6b, we find that in the range of 0 < K < 0.2, for each φ k, the Poisson’s ratio v increases with K, while for each K, v nearly keeps constant for varied φ k. This may imply that v is not sensitive to the gas-saturated porosity in kerogen.

Fig. 6
figure 6

Calculated templates showing geo-mechanical properties a Young’s modulus E and b Poisson’s ratio v for the variations in K and φ k in the shale

Full size image

5 The effect of K and φ k on seismic AVO responses

In Fig. 7, we demonstrate the seismic AVO responses resulting from the variations in K and φ k. For the geological model shown in Fig. 7a, b illustrates how the variations in K and φ k affect the acoustic impedance I p of the shale based on the rock physics model. We consider two cases as indicated by blue and red solid circles in Fig. 7b. The blue solid circle represents values of K and φ k of 0.05 and 0.1, respectively, while the red solid circle corresponds to the values of 0.15 and 0.3.

Fig. 7
figure 7

a The model in which a chalk layer overlays on a shale layer. b Calculated acoustic impedance I p of the shale varying with K and φ k. Two cases with different properties are highlighted. c Seismic AVO responses corresponding to the two cases in (b), with the same color scheme

Full size image

The properties of the overlaid chalk are V p = 4100 m/s, V s = 2500 m/s, and ρ = 2800 kg/m3. We calculate AVO responses using numerical solutions of the Zoeppritz equations and display the results in Fig. 7c by the same colors for the cases in Fig. 7b. We observe significant differences in AVO responses resulting from the variations in K and φ k of the shale. Reflection amplitudes are negative for normal incidence, and their absolute values decrease with increasing incidence angles, which corresponds to the fifth type AVO responses (Roger and Robert 2010). Meanwhile, normal incidence amplitudes and AVO gradients have relatively higher values for higher kerogen content and kerogen porosity for low wave impedance shale (in red).

Figure 8 illustrates the calculated AVO intercept P and gradient G corresponding to the model in Fig. 7a for the variations in K and φ k. In Fig. 8a, we can see that the values of intercept P are negative and its absolute values increase with increasing K and φ k, which has similar trends as the velocities and density as shown in Fig. 5. In Fig. 8b, the AVO gradient G represents positive and increases with increasing K and φ k. These predictable trends of AVO responses can be used for the characterization of the variations in K and φ k.

Fig. 8
figure 8

Templates illustrating a AVO intercept P and b gradient G for the variations in K and φ k, corresponding to the geological model and acoustic impedance variations in Fig. 7a and b

Full size image

6 Conclusions

We have developed a rock physics model based on the effective medium theories for the characterization of the effects of kerogen content K and kerogen porosity φ k on elastic and geo-mechanical properties in the organic-rich shale. The parameter φ k indicates the proportion of hydrocarbon-saturated pores generated within kerogen. Rock physics modeling results show that the increases in K and φ k significantly reduce the values of V p, V s, and ρ and the effects of K and φ k are correlated with each other. Due to low velocities and density, the increase in K decreases velocities and density and the presence of φ k enhances such impacts. For the case of K < 0.05, in this study, the effect of φ k on the elastic properties is not obvious, while for K > 0.05, the increase in φ k significantly decreases velocities and density of shales. In the range of 0 < K < 0.2, Poisson’s ratio v is not sensitive to the gas-saturated porosity in kerogen. AVO modeling reveals that for the model in this work, reflection amplitudes for normal incidence are negative and the corresponding absolute values decrease with increasing incidence angles, which represents the fifth type AVO responses. For increasing K and φ k, the absolute values of intercept P and gradient G increase. The predictable trends in AVO responses can be used for the characterization of the variations in K and φ k.