Abstract
The optimal design and operation at large scale of a continuous fermentation process including a biological reactor/photobioreactor and a gravity settler with partial recycle and purge of the biomass are addressed. The proposed method is developed with reference to microalgae (Scenedesmus obliquus) cultivation, but it can be applied to any fermentation process as well as to activated sludge wastewater treatment. A procedure is developed to predict the effect of process variables, mainly the recycle ratio (R), the solid retention time (θ c ), the reactor residence time (θ), and the ratio between feed and purge flow rates (F I /F W ). It includes a simple steady-state model of the two units coupled in the process and the experimental measurement of basic kinetic data, in both the bioreactor and the settler, for the tuning of model parameters. The bioreactor is assumed as perfectly mixed, and a rigorous gravity-flux approach is used for the settler. The process model is solved in terms of dimensionless variables, and plots are given to allow sensitivity analyses and optimization of operating conditions. A discussion about washout is presented, and a simple method is outlined for the calculation of the minimum values of residence time (θ min ) and recycle ratio (R min ) and of the maximum allowed recycle ratio (R max,operating ) and biomass purge rate (F Wmax ). In particular, it is shown that the system is sensitive to the concentration of biomass lost from the top of the settler (C X S). The proposed method can be useful for the design and analysis of large-scale processes of this type.








Similar content being viewed by others
Abbreviations
- I, E, U, S, R and W :
-
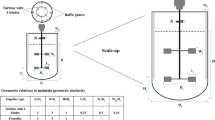
When associated with variables cited below they refer to the streams of the process including a reactor and settler, as represented in Fig. 1.
- C i :
-
Concentration of component i (g L−1 or kg m−3 for solid concentration)
- θ :
-
Residence time or hydraulic retention time (HRT) (day)
- r i :
-
Rate of production or consumption of component i (g L−1 day−1)
- K M :
-
Monod saturation constant for substrate (g L−1)
- k :
-
Maximum specific growth rate (day−1)
- k d :
-
Specific rate of cell death (day−1)
- F :
-
It indicates the volumetric flow rates of the different streams in the process
- M :
-
It indicates the mass flow rates of the different streams in the process (kg day−1)
- F W :
-
Cell purge flow rate (m3 day−1)
- F R :
-
Recycle flow rate (m3 day−1)
- F I :
-
Inlet flow rate (m3 day−1)
- θ c :
-
Solid retention time (SRT) (day)
- \( {\theta}_c^{wo} \) :
-
Wash-out time for SRT (day)
- Y X/S :
-
Apparent yield coefficient for substrate-to-biomass conversion (g g−1)
- V R :
-
Effective volume of the reactor (m3)
- R min :
-
Minimum recycle ratio (−)
- R max,operating :
-
Maximum recycle ratio that permits an adequate settler operation (efficient sedimentation), considering v = 0 at the bottom of the settler
- R C :
-
Critical recycle ratio, i.e., maximum recycle ratio to permit that the settler does not collapse
- G u :
-
Convective solid flux in the settler (kg m−2 day−1)
- G v :
-
Gravitational solid flux in the settler (kg m−2 day−1)
- Gapp :
-
Applied solid flux in the settler (kg m−2 day−1)
- u :
-
Convective settling velocity
- A :
-
Settler surface area
- v :
-
Gravity settling velocity (m h−1)
References
Petre E, Selisteanu D (2013) A multivariable robust-adaptative control strategy for a recycled wastewater treatment bioprocess. Chem Eng Sci 90:40–50
D’Antonio G, Carbone P (1987) Verifica sperimentale della teoria del flusso solido. Ing Sanit 325–336
Sardo F, Indelicato S (1995) Verifica della teoria del flusso solido in un impianto a fanghi attivi a portata costante. Ing Ambient 24(10):584–587
Yuan Q, Sparling R, Oleszkiewicz JA (2009) Waste activated sludge fermentation: Effect of solids retention time and biomass concentration. Water Res 43:5180–5186
Alcantara C, Dominguez JM, Garcia D, Blanco S, Perez R, Garcia-Encina PA, Munoz R (2015) Evaluation of wastewater treatment in a novel anoxic-aerobic algal-bacterial photobioreactor with biomass recycling through carbon and nitrogen mass balances. Bioresour Technol 191:173–186
Amanatidou E, Samiotis G, Bellos D, Pekridis G, Trikoilidou E (2015) Net biomass production under complete solids retention in high organic load activated sludge process. Bioresour Technol 182:193–199
Nges IA, Liu J (2010) Effects of solid retention time on anaerobic digestion of dewatered-sewage sludge in mesophilic and thermophilic conditions. Renew Energy 35:2200–2206
Lee I, Parameswaran P, Rittmann BE (2011) Effects of solid retention time on methanogenesis in anaerobic digestion of thickened mixed sludge. Bioresour Technol 102:10266–10272
Narodolawsky M, Mittmannsgruber H, Nagl W, Moser A (1988) Modelling of alcohol fermentation in a tubular reactor with high biomass recycle. Bioprocess Eng 3:135–140
Oliveira SC, Castro HF, Visconti AES, Giudici R (2015) Mathematical modeling of a continuous alcoholic fermentation process in a two-stage tower reactor cascade with flocculating yeast recycle. Bioprocess Biosyst Eng 38:469–479
Meyer CL, Papoutsakis ET (1989) Continuous and biomass recycle fermentations of Clostridium acetobutylicum. Bioprocess Eng 4:49–55
Lee D, Li V, Noike T (2010) Influence of solids retention time on continuous H2 production using membrane bioreactor. Int J Hydrog Energy 32:52–60
Grøn S, Morcel C, Emborg C, Biedermann K (1995) Cell recycling studies for α-amylase production by Bacillus amyloliquefaciens. Bioprocess Eng 14:23–31
Grøn S, Biedermann K, Emborg C (1996) Production of proteinase A by Saccharomyces cerevisiae in a cell-recycling fermentation system: experiments and computer simulations. Appl Microbiol Biotechnol 44:724–730
Park JBK, Craggs RJ, Shilton AN (2011) Recycling algae to improve species control and harvest efficiency from a high rate algal pond. Water Res 45:6637–6649
Sforza E, Gris B, Silva CEF, Morosinotto T, Bertucco A (2014) Effects of light on cultivation of Scenedesmus obliquus in batch and continuous flat plate photobioreactor. Chem Eng Trans 38:211–216
Sing SF, Isdepsky A, Borowitzka MA, Lewis DW (2014) Pilot-scale continuous recycling of growth medium for the mass culture of a halotolerant Tetraselmis sp. in raceway ponds under increasing salinity: a novel protocol for commercial microalgal biomass production. Bioresour Technol 161:47–54
Depraetere O, Pierre G, Deschoenmaeker F, Bodri H, Foubert I, Leys N, Markou G, Wattiez R, Michaud P, Muylaert K (2015) Harvesting carbohydrate-rich Arthrospira platensis by spontaneous settling. Bioresour Technol 180:16–21
Kosinska K, Miskiewicz T (2009) Performance of an anaerobic bioreactor with biomass recycling continuously removing COD and sulphate from industrial wastes. Bioresour Technol 100:86–90
Uduman N, Qi Y, Danquah MK, Forde GM, Hoadley A (2010) Dewatering of microalgal cultures: a major bottleneck to algal-based fuels. J Renewable Sustainable Energy 2:12701–12715
Park JBK, Craggs RJ, Shilton AN (2013) Enhancing biomass energy yield from pilot-scale high rate algal ponds with recycling. Water Res 47:4422–4432
Zhu L (2015) Biorefinery as a promising approach to promote microalgae industry: an innovative framework. Renew Sust Energ Rev 41:1376–1384
Barros AI, Gonçalves AL, Simoes M, Pires JCM (2015) Harvesting techniques applied to microalgae: a review. Renew Sust Energ Rev 41:1489–1500
Lund JWG (1951) A sedimentation technique for counting algae and other organisms. Hydrobiologia 3(4):390–394
Salim S, Bosma R, Vermué MH, Wijffels RH (2011) Harvesting of microalgae by bio-flocculation. J Appl Phycol 23:849–855
Smith BT, Davis RH (2012) Sedimentation of algae flocculated using naturally-available magnesium-based flocculants. Algal Res 1(1):32–39
Liu J, Tao Y, Wu J, Zhu Y, Gao B, Tang Y, Li A, Zhang C, Zhang Y (2014) Effective flocculation of target microalgae with self-flocculating microalgae induced by pH decrease. Bioresour Technol 167:367–375
Rawat I, Kumar RR, Mutanda T, Bux F (2013) Biodiesel from microalgae: A critical evaluation from laboratory to large scale production. Appl Energy 103:444–467
Du J, McGraw A, Lorenz N, Beitle RR, Clausen EC, Hestekin JA (2012) Continuous fermentation of Clostridium tyrobutyricum with partial cell recycle as a long-term strategy for butyric acid production. Energies 5:2835–2848
Bertucco A, Beraldi M (2014) Sforza E (2014) continuous microalgal cultivation in a laboratory-scale photobioreactor under seasonal day-night irradiation: Experiments and simulation. Bioprocess Biosyst Eng 37:1535–1542
Silva CEF, Gris B, Bertucco A (2016) Simulation of microalgal growth in a continuous photobioreactor with sedimentation and partial biomass recycling. Braz J Chem Eng 33(4):773–781
Fernandes BD, Mota A, Teixeira JA, Vicente AA (2015) Continuous cultivation of photosynthetic microorganisms: approaches, applications and future trends. Biotechnol Adv 33(6):1228–1245
Barbera E, Sforza E, Bertucco A (2015) Maximizing the production of Scenedesmus obliquus in photobioreactors under different irradiation regimes: experiments and modeling. Bioprocess Biosyst Eng 38:2177–2188
Rippka R, Deurelles J, Waterbury JB, Herdman M, Stainer RY (1979) Generic assignments, strain histories and properties of pure cultures of cyanobacteria. J Gen Microbiol 111: 1–61.
Sundstrom DW, Klei HE (1979) Wastewater treatment. The University of Connecticut - Prentice Hall, Englewood Cliffs
Sforza E, Enzo M, Bertucco A (2013) Design of microalgal biomass production in a continuous photobioreactor: An integrated experimental and modeling approach. Chem Eng Res Des 92(6):1153–1162
Borzani W (2001) In: Borzani W, Schmidell W, Lima UA, Aquarone E (Coords.) Biotecnologia Industrial: VOLUME 2—Biotecnologia Industrial., Bluche, Sao Paulo, 560 p
Bertucco A, Volpe P, Klei HE, Anderson TF, Sundstrom DW (1990) The stability of activated sludge reactors with substrate inhibition kinetics and solids recycle. Water Res 24(2):169–174
Peperzak L, Colijn F, Koeman R, Grieskes WWC, Joordens JCA (2003) Phytoplankton sinking rates in the Rhine region of freshwater influence. J Plankton Res 25(4):365–383
Caciki A, Bayramoglu M (1995) An approach to controlling sludge age in the activated sludge process. Water Res 29(4):1093–1097
Bai S, Srikantaswamy S, Shivakumar D (2010) Urban wastewater characteristic and its management in urban areas—a case study of Mysore City, Karnataka, India. J Water Resour Prot 2:717–726
Mittal A (2011) Biological wastewater treatment. Water Today, August: 32–44
MPCA (2002) Design flow and loading determination guidelines for wastewater treatment plants: water/wastewater technical review and guidance. Minnesota Pollution Control Agency
Da Silva TL, Reis A (2015) Scale-up problems for the large scale production of algae. In: Das D (ed) Algal Biorefinery: an integrated approach. Springer, Cham, pp 125–149
Gupta PL, Lee S, Choi H (2015) A mini review: photobioreactor for large scale algal cultivation. World J Microbiol Biotechnol 31(9):1409–1417
Rawat I, Kumar RR, Mutanda T, Bux F (2013) Biodiesel from microalgae: a critical evaluation from laboratory to large scale production. J Appl Energy 103:444–467
Zhang T, Hu H, Wu Y, Zhuang L, Xu X, Wang X, Dao G (2016) Promising solutions to solve the bottlenecks in the large-scale cultivation of microalgae for biomass/bioenergy production. Renew Sust Energ Rev 60:1602–1614
Woo SH, Jeon CO, Yun Y, Choi H, Lee C, Lee DS (2009) On-line estimation of key processes variables based on kernel partial least squares in an industrial cokes wastewater treatment plant. J Hazard Mater 161(1):538–544
Bezzaoucha S, Marx B, Maquin D, Ragot J (2013) Non linear joint state and parameter estimation: application to a wastewater treatment plant. Control Eng Prat 21(10):1377–1385
Busch J, Elixmann D, Kuhl P, Gerkens C, Schloder JP, Back HG, Marquadt W (2013) State estimation of large-scale wastewater treatment plants. Water Res 47(13):4774–4787
Tomita RK, Park SW (2009) Evolutionary multi-objective optimization of an activated sludge process. Comput Aid Chem Eng 27:747–752
Qiao J, Hou Y, Han H (2018) Optimal control for wastewater treatment process based on an adaptive multi-objective differential evolution algorithm. Neural Comput Applic 1–14. https://doi.org/10.1007/s00521-017-3212-4
Lou I, Zhao Y (2012) Sludge bulking prediction using principal component regression and artificial neural network. Math Probl Eng 2012:237693 17 pages
Simion C, Chenaru O, Florea G, Lozano JI, Nabulsi S, Reis M, Cassidy J (2016) Decision support system based on fuzzy control for a wastewater treatment plant. Int J Environ Sci 1:344–349
Samsudin SI, Rahmat MF, Wahab NA (2014) Nonlinear PI control with adaptive interaction algorithm for multivariable wastewater treatment process. Math Probl Eng 2014:475053 13 pages
Wahab HF, Katebi R, Villanova R (2012) Comparisons of nonlinear estimators for wastewater treatment plants. In: 20th Mediterranean Conference on Control & Automation (MED), Barcelona, Spain, July 3-6.
Acknowledgements
The authors thank CNPq, Brazil (National Research Council of Brazil)—Process number 249182/2013-0—for resources and fellowship.
Funding
This study was funded by CNPq, Brazil (National Research Council of Brazil) Process number 249182/2013-0.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Ethical Approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Electronic supplementary material
ESM 1
(DOCX 188 kb).
Appendix. Gravity Solid Flux Theory
Appendix. Gravity Solid Flux Theory
The total flux of solids in a gravity settler (G T ) is given by the following:
where
- G u :
-
Convective solid flux (kg m−2 day−1)
- G v :
-
Gravitational solid flux (kg m−2 day−1)
- C :
-
Solid concentration (in this case, biomass concentration) (kg/m3)
- u :
-
Convective settling velocity
- A :
-
settler surface area
- v :
-
Settling velocity by gravity
In the settler, the value of C X increases from C X U to C X R. The solid fluxes are a function of the solid concentration according to Fig. S2 (Supplementary File), where the occurrence of a minimum value is evidenced.
The solid flux applied to the settler is given by the following:
For a correct settler operation, it is necessary that G app < G T , whatever the value of C X within the settler (between C X U and C X R). The dependence of G T on C X , for a pre-established u value, is given by the following:
Applying the first and second derivatives analysis to find the minimum point, we obtain the following:
where C L indicates the critical biomass concentration corresponding to the maximum, or limiting, solid flux (G L ) ensured by the settler.
Equation (41) cannot be resolved analytically; however, using Eq. (42), a relationship easier to work can be found:
By replacing Eq. (43) in Eq. (41), we have the following:
The value of the limiting flow of solids (G L ) can be calculated from Eq. 40 with u given by Eq. 36:
According to the literature [2], if it is assumed that v = 0 at the bottom of the settler, Eq. (45) in combination with Eq. (34) yields the following:
By expressing u from Eq. (41) and introducing it in Eq. (46), it can be obtained that:
Using condition I above (Eq. 43), it results to the following:
Equation (47) is a second-degree equation in C L :
whose roots are as follows:
Only C L ′ is the useful root, as C L ″ does not respect conditions I and III. A correct operation of the settler requires that:
according to which, it can be finally obtained that:
where C L can be expressed by Eq. (50) as a function of C X R, which is in turn a function of C X U, R, θ, and θ c according to Eq. (15). In summary, if F I , A, C X U, θ, and θ c are known, a single value of R can be calculated from Eq. (53).
The recycle ratio is indeed the key variable: if R value is too high, the convective velocity will be dominant in the settler and will not allow to thicken the solid enough for the sedimentation. A limiting situation will be reached when C X U = C X R (rupture of the reactor operation). To calculate this value, which is called critical recycle ratio (R C ), it is sufficient to express \( {C}_X^R \) from a mass balance around the settler:
and to apply Eq. (48) (condition III).
Two cases can be considered to calculate the R c value:
-
1.
When C X S = 0, it results to the following:
-
2.
When C X S ≠ 0, we have the following:
In any case, the system must be operated with the following:
and Eq. (53) holds under this condition only.
The value of C X R min,operating , i.e., the minimum biomass concentration to correctly operate the settler, is given by Eq. (48) (condition III), then from Eq. (15) R max,operating can be calculated:
It is noteworthy that the procedure outlined above assumes v = 0 at the bottom of the settler. If this condition is not verified, Eq. (46) does not hold any more. Instead, by combining Eq. (45) with Eq. (36), where the value of u is expressed by Eq. (41), it can be obtained that:
This equation can be solved numerically for C L , because v0, α, and C X R(θ c ) are fixed values, depending on C L , only. In this case, the value of C X R min,operating cannot be expressed analytically as for Eq. (47). These concepts are qualitatively shown in Fig. S3 (Supplementary File).
Rights and permissions
About this article
Cite this article
de Farias Silva, C.E., Bertucco, A. A Two-Stage System for the Large-Scale Cultivation of Biomass: a Design and Operation Analysis Based on a Simple Steady-State Model Tuned on Laboratory Measurements. Bioenerg. Res. 11, 398–413 (2018). https://doi.org/10.1007/s12155-018-9905-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12155-018-9905-4